9.2.3 Кодирование в биологических структурах

Исследования показали, что и внутри всех биологических организмов тоже существует информационный обмен. Примером этого является информационный обмен осуществляемые на уровне клеток. В середине прошлого столетия был открыт генетический код. Оказалось, что все существа на планете Земля состоят из клеток, основой которых являются белки, а белки образуются из аминокислот. Каждая аминокислота образуется из так называемых нуклеотидов или триплетных комбинаций, азотистых оснований мРНК, а именно цитозина, аденина и гуанина.

При этом каждой аминокислоте соответствует свой триплет, свой набор нуклеотидов, фактически своя кодовая комбинация. Биологи называют эти комбинации кодонами, а мы в нашем курсе теории информации употребляли термин кодовая комбинация.

Таблица 7

2-е положение

U

C

A

G

1-е положение

U

UUU

Phe

UCU

Ser

UAU

Tyr

UGU

Cys

U

3-е положение

UUC

Phe

UCC

Ser

UAC

Tyr

UGC

Cys

C

UUA

Leu

UCA

Ser

UAA

ochre

UGA

opal

A

UUG

Leu

UCG

Ser

UAG

amber

UGG

Try

G

C

CUU

Leu

CCU

Pro

CAU

His

CGU

Arg

U

CUC

Leu

CCC

Pro

CAC

His

CGC

Arg

C

CUA

Leu

CCA

Pro

CAA

Gln

CGA

Arg

A

CUG

Leu

CCG

Pro

CAG

Gln

CGG

Arg

G

A

AUU

Ile

ACU

Thr

AAU

Asn

AGU

Ser

U

AUC

Ile

ACC

Thr

AAC

Asn

AGC

Ser

C

AUA

Ile

ACA

Thr

AAA

Lys

AGA

Arg

A

AUG*

Met

ACG

Thr

AAG

Lys

AGG

Arg

G

G

GUU

Val

GCU

Ala

GAU

Asp

GGU

Gly

U

GUC

Val

GCC

Ala

GAC

Asp

GGC

Gly

C

GUA

Val

GCA

Ala

GAA

Glu

GGA

Gly

A

GUG*

Val

GCG

Ala

GAG

Glu

GGG

Gly

G

Триплетные комбинации азотистых оснований мРНК: тимин, цитозин, аденин, гуанин (U, C, A, G) определяют следующие аминокислоты: Phe – фениланин, Leu – лейцин, Ile – изолейцин, Met – метионин, Val – валин, Ser – серин, Pro – пролин, Thr – треонин, Ala – аланин, Tyr – тирозин, His – гистидин, Gln – глутамин, Asn – аспарагин, Lys – лизин, Asp – аспарагиновая кислота, Glu – глутаминовая кислота, Cys – цистеин, Try – триптофан, Arg – аргинин, Gly –глицин.

Звездочкой обозначены стартовые кодоны, а триплеты ochre, amber, opal действуют как стоп кодоны.

Природа так распорядилась, что одной и той же аминокислоте соответствует разные кодоны, разные кодовые комбинации из приведенной таблицы 7. Это легко заметить, причём некоторым аминокислотам соответствует одно количество триплетных кодовых комбинаций, а другим аминокислотам другое количество. Почему так, к сожалению, на сегодняшний день не знает никто, но, наверное, у природы были основания для такого решения. Возможно в будущем нам удастся открыть эти секреты.

Используемый код не является префиксным, поэтому для обеспечения синхронизации, ровно также как в простом телеграфном аппарате, в генетическом коде предусмотрены стартовые кодоны и стоповые кодоны. Генетический код - это старт-стопный код. Подобная информация ещё раз доказывает универсальность теории информации и значимость для самых разных областей её применения.

Обратимся еще к одному очень интересному применению. Рассмотрим такие объекты как человек - обезьяна и далее по ниспадающей, доходя до достаточно примитивных биологических существ, таких как червячок и т.д.

Если человека закодировать как число 16, а рядом стоящую по степени развития обезьянку числом 15 и т.д., то червячок получит число 1. Если теперь мы постараемся измерить отличия между человеком и обезьяной, измеряя это различием между десятичными числами, то эти отличия между человеком и обезьянкой будут меньше по сравнению с отличием между человеком и червяком.

Теперь десятичные числа 16, 15, 14 и т.д. мы представим в двоичной системе счисления. Тогда человеку будет поставлена в соответствие кодовая комбинация 10000, обезьяне 01111, а червяку- комбинация 00001 (рис.23).

Теперь мы попробуем также сравнить разницу между числами, но выяснится, что между человеком и червячком несовпадение будет в 2-х позициях, тогда как несовпадение между человеком и обезьяной будет в 5-ти событиях. Ситуация абсолютно диаметрально противоположна, по сравнению с предыдущей.

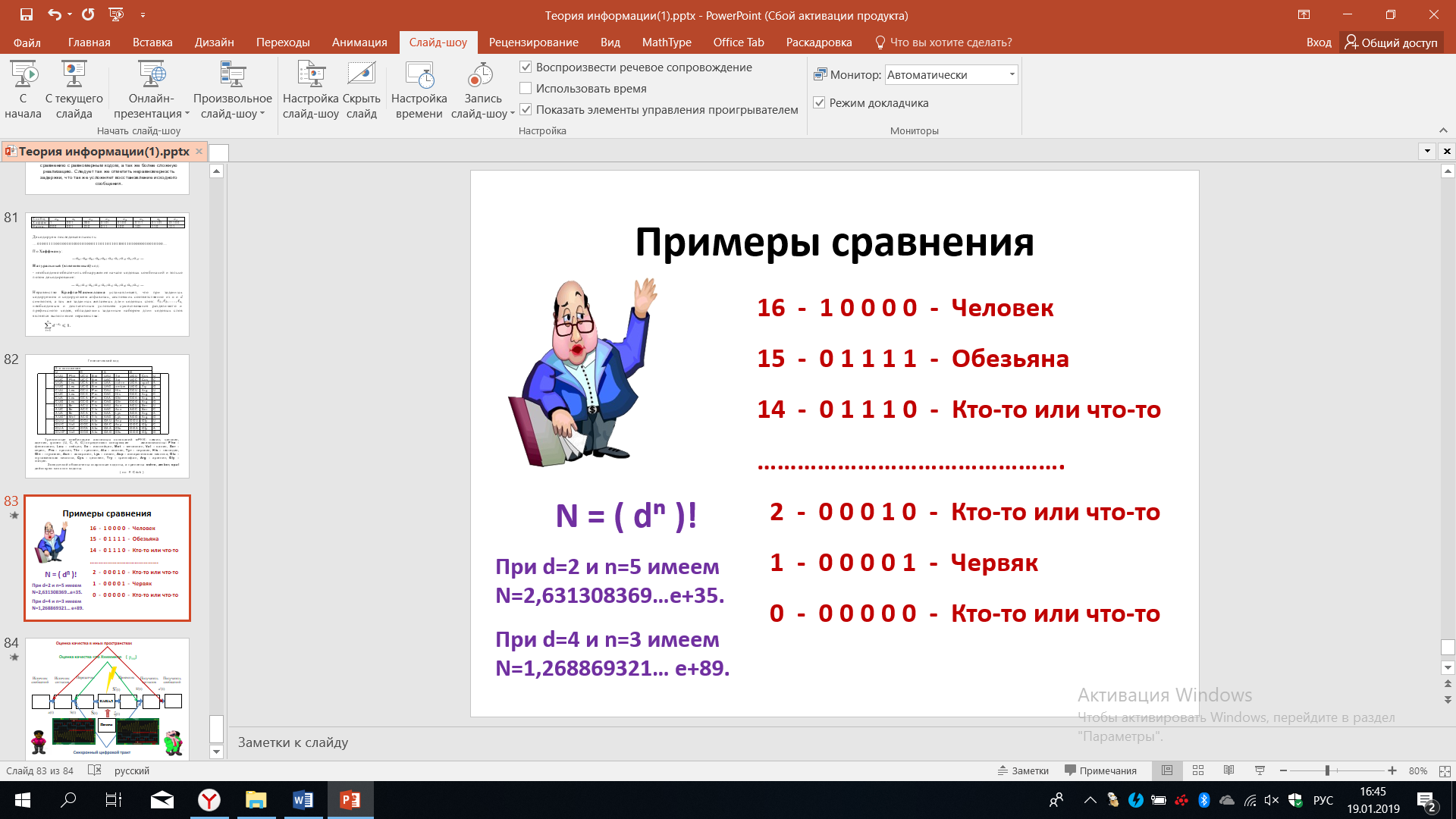
Рисунок 23 – Примеры сравнения

Это говорит о том, что, осуществляя сравнение различных объектов между собой, надо очень точно и правильно определить метрику того пространства в котором осуществляются эти сравнения, иначе в десятичных числах между человеком и обезьяной будет минимальное различие, тогда как при сравнение двоичных чисел, наоборот, максимальное.

Это был один из способов кодирования. Можно было бы поменять местами эти двоичные числа, с точки зрения скорости кодирования ничего не изменится, и в первом, и во втором случае будет затрачено одно и тоже количество символов для кодирования сообщений. Стало быть, энтропия в данном случае будет одинакова для этих источников. Но тогда как быть с тем, что количество вариантов перестановок при кодировании определяется по формуле , где основание кода - это количество символов в кодовой комбинации (рис.23).

Однако природа остановилась на каком-то одном варианте, опять же мы не знаем причин всего этого и надеемся на то, что в будущем появятся какие-то вразумительный ответы на эти вопросы. Но в данном случае это является примером того, что при анализе систем связи, основой которых является теории информации, нам следует расширить блок-схему, придуманную предложенную Клодом Шенноном.

Рассмотрим рисунок 24.

Рисунок 24 – Блок-схема СПИ с оценкой в различных метрических пространствах.

В данной схеме, в отличие от той схемы, которая была нами рассмотрена (ее в свое время предложил Клод Шеннон) между источником сообщений и передатчиком появился ещё один блок - источник сигнала. На приёме между приемником и получателем сообщение появился получатель сигналов. Это сделано для того, чтобы мы могли оценить те особенности, которые включает в себя аналого-цифровое преобразование. А в общем случае при преобразовании сообщений в сигналы в разных метрических пространствах.

На сегодняшний день наибольшей эффективностью обладают цифровые системы передачи, где по каналу связи передается последовательность единиц и нулей с помощью определенных методов. Тогда между передатчиком и приемником мы можем определить так называемый синхронный цифровой тракт, где на входе передатчика цифровая последовательность нулей и единиц, а на выходе приемника соответственно последовательность также нулей и единиц, но уже прошедших через канал, передатчик, приемник и, возможно, подвергшийся влиянию помех.

Поскольку здесь мы имеем дело с двоичным сигналом, то оценивать качество передачи или качество приёма мы можем в пространстве Хемминга, сравнивая последовательности между собой и выявляя различия. Там, где должен был быть 0, может появится 1 и наоборот. Хорошей оценкой для этого является количество таких несовпадений, которые измеряются с помощью показателя верности передачи или вероятности ошибки.

Вероятность ошибки в данном случае равняется количеству неверно принятых двоичных символов, отнесенных к общему количеству принимаемых двоичных символов. Однако эти двоичные сигналы далее преобразуется в сообщения, а уже сообщения сравниваются между собой в совершенно ином пространстве. Примеры этого мы видели, поэтому, говоря о сравнении принятого сообщения из синхронного цифрового тракта с переданным, мы должны говорить о сравнении в том пространстве, в той метрике, которая адекватна этим сообщениям. Если при сравнение цифровых сигналов (двоичных сигналов) мы использовали пространство Хемминга, то здесь нужно использовать что-то другое, в зависимости от того, каким является сообщение, в какой метрике, в каком пространстве это сообщение представимо.