
Sb96244
.pdf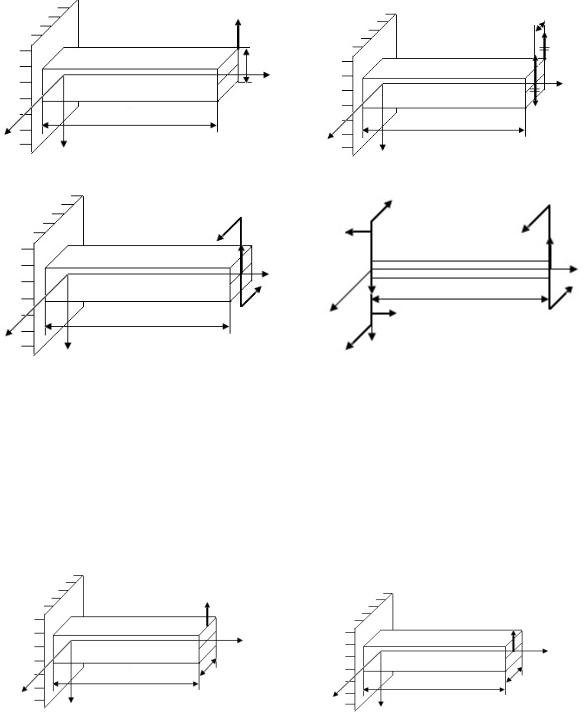
|
|
P |
|
|
|
a |
|
B |
|
|
|
P |
|
|
|
|
|
|
||
|
O x |
|
|
|
P |
|
|
|
|
|
P x |
||
|
l |
|
|
|
l |
|
y |
|
|
|
|
||
z |
|
y |
z |
|
|
|
|
а |
|
|
|
б |
|
|
|
|
|
|
|
|
|
M1 |
P |
MA2 |
MA1 |
|
M1 |
|
|
|
|
|
P |
|
|
|
O |
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
AV |
l |
||
|
|
|
||||
|
l |
|
y |
|
|
|
|
|
|
z |
|
|
|
y |
z |
|
|
|
|
|
|
|
|
|
|
||
|
в |
|
|
|
г |
|
|
|
|
|
|
|
|
|
Рис. 38. Схемы приведения силы Р к оси стержня |
|
||||
Силу P, приложенную в точке В (рис. 39, |
а), можно перемещать по |
|||||
линии действия. От этого характер нагрузки на систему не изменится. Переместим эту силу P в точку О (рис. 39, б). Опорные реакции в стержне
определим, |
используя |
условия |
статического |
равновесия |
∑ |
in=1 Zi = 0 , |
|||
∑ |
in=1 Miy, A |
= 0: AV = –P, MA = P. |
|
|
|
|
|||
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
||
|
|
|
|
B |
|
|
|
||
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
O |
x |
||
|
y |
|
l |
2a |
|
l |
|||
|
z |
y |
2a |
|
|||||
|
|
|
|
z |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
б |
|
|
|
|
|
|
Рис. 39. Схемы приведения силы Р к оси стержня |
|
|
|
|||
|
Определим внешние силы, действующие на стержень при приложении |
||||||||
силы P в точке В (рис. 40, а). Воспользовавшись принципом Сен-Венана, |
|||||||||
приведем силу |
в точку O (рис. 40, б). |
|
|
|
|
||||
|
Получим пару сил с моментом M = Pa, изгибающим стержень в |
||||||||
плоскости |
xOy |
относительно оси |
z, и силу P, |
растягивающую |
стержень |
||||
(рис. 40, в). |
|
|
|
|
|
|
|
|
|
21
Из |
условий |
статического |
равновесия |
n |
n |
|
z, A |
||
∑i=1 Zi = 0 , ∑i=1 Mi |
= 0 |
||||||||
получим MA = M = Pa, AH = P (рис. 40, г). |
|||||||||
|
|
B |
a P |
|
|
|
B |
P |
|
|
|
O |
x |
|
|
P |
O P x |
||
|
|
y |
|
l |
|
|
|||
y |
l |
2a |
|
z |
2a |
|
|||
|
|
|
|
|
|||||
|
z |
|
|
|
|
|
|
||
|
|
|
|
|
б |
|
|
||
|
|
|
|
|
|
|
|
||
|
а |
|
|
|
|
|
|
|
|
|
|
|
M |
AH |
MA |
|
|
M |
|
|
|
|
|
|
|
|
|||
|
|
|
P |
|
|
|
|
P x |
|
|
|
O |
x |
y |
|
l |
|
||
|
|
|
|
|
|||||
y |
l |
2a |
|
|
|
|
|||
|
|
z |
|
|
|
||||
z |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
г |
|
|
||
|
в |
|
|
|
|
|
|
||
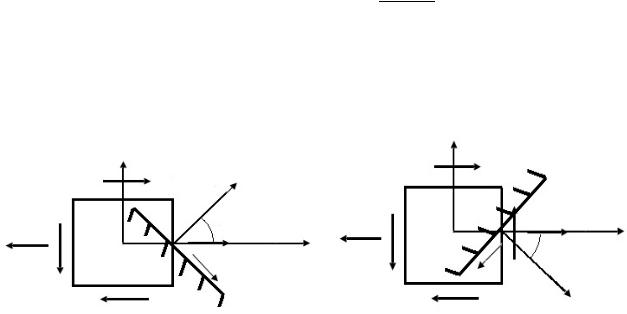
Рис. 40. Схемы приведения силы Р к оси стержня (принцип Сен-Венана)
Используя принцип Сен-Венана, приведем силы P, приложенные в точках В, С, к оси стержня. Приведение сил определяет нагружение стержня, показанное на рис. 41.
|
|
|
|
|
|
P a |
P |
|
|
|
P |
|
|
C |
B |
|
|
C |
B |
|
|
|
|
|
|
|
|
P |
O P x |
||
|
|
P |
O |
x |
|
||
|
l/2 |
l/2 |
l |
2a |
|||
y |
l |
2a |
|
||||
|
|
||||||
|
z |
|
|
y |
z |
|
|
|
|
а |
|
|
|
б |
|
|
|
Рис. 41. Схемы приведения силы Р к оси стержня |
|
||||
Моменты пар сил равны по величине Pa, но скручивают стержень в разных направлениях. Из условия статического равновесия ∑ni=1 Zi = 0 ,
∑ni=1 Mix, A = 0 определим опорные реакции MA = 0, AV = 0.
Определение внутренних усилий в стержнях
Р.15. 1. Из условия статического равновесия определим опорную реакцию AH в стержне (рис. 42, а):
22
n
Xi = 0 ; –AH + q·10a + P – q·2a = 0, AH = 13qa.
i=1
2. Определяем число грузовых участков. 3. На каждом участке, не захватывая его границы, проводим сечение. 4. В сечении представляем внутренние силовые факторы в соответствии с правилами знаков.
q |
P |
q |
AH |
|
|
5a |
8a |
|
|
|
|
|
10a |
|
|
a |
|
13qa |
|
|
N |
8qa |
|
3qa |
|
|
|
|
−2qa x
б
Рис. 42. Схема стержня и эпюр нормальных сил
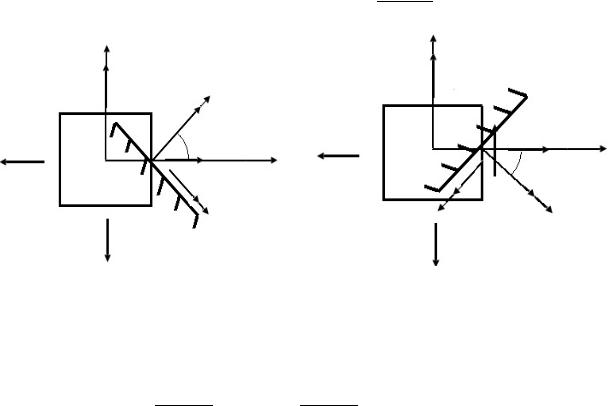
5. Рассчитываем значения внутренних силовых факторов на границе участков. 6. В соответствии с проведенными расчетами строим эпюр нормальных сил (рис. 42, б).
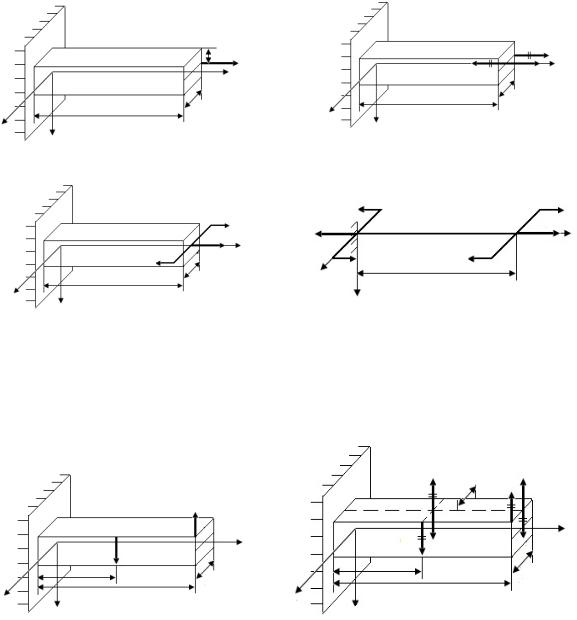
Из условия статического равновесия определим опорные реакции AH,
MA в стержне, показанном на рис. 43, а:
n
Zi = 0 ; –AV + q·10a = 0, AV = 10qa,
i=1
n
Miy, A = 0 ; MA – q·10a·10a + M = 0, MA = 50qa2.
i=1
Далее выполняем работу в соответствии с п. 2−5 задачи Р.15. По результатам вычислений Qz и My на границах грузовых участков построены эпюры поперечных сил Qz (рис. 43, б) и изгибающих моментов My
(рис. 43, в).
23
AV |
q |
|
|
|
|
|
|
||
MA |
|
|
M = 50qa2 |
|
5a |
10a |
5a |
||
|
a
10qa
Qz
x
б
−50 qa2
My
x
50qa2
в
Рис. 43. Схема стержня и эпюры поперечных сил и изгибающих моментов
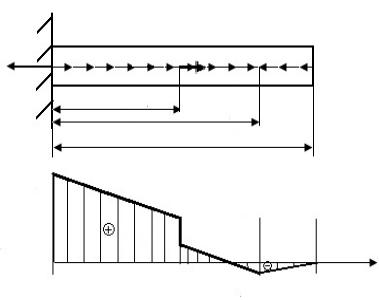
Из условия статического равновесия определим опорный момент MA в
стержне, показанном на рис. 44, а:
n
Mix, A = 0 ; MA – m·3a + M1+ M2 = 0, MA = 2ma.
i=1 |
|
|
|
|
|
|
M1 = 2ma |
|
M2 = 3ma |
MA |
|
m |
m |
m |
|
|
a |
2a |
a |
|
|
3ma |
a |
|
|
2ma |
|
2ma |
|
|
ma |
|
||
Mx |
|
|
|
|
|
|
|
|
x
−ma
б
Рис. 44. Схема стержня и эпюр крутящих моментов
24
Далее выполняем работу в соответствии с п. 2−5 задачи Р.15. По результатам вычислений Mx на границах грузовых участков строим эпюр крутящих моментов (рис. 44, б).
Основные уравнения механики твердого деформированного тела
Р.16. Напряженное состояние в окрестности точки, а, следовательно, и главные напряжения σ1, σ2, σ3 не могут меняться при изменении системы координат, кубическое уравнение должно быть инвариантно к преобразованию системы координат.
Р.17. Коэффициенты кубического уравнения ΘI, ΘII, ΘIII называют инвариантами тензора напряжений, потому что их значения не зависят от выбранной системы координат.
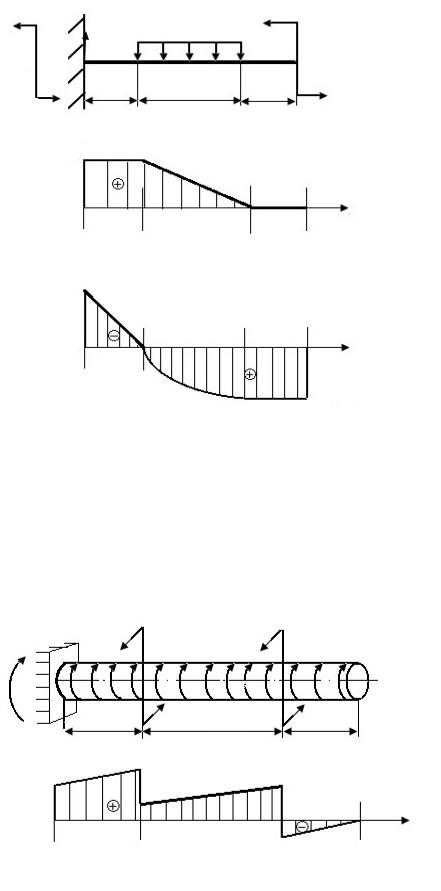
Р.18. При плоском напряженном состоянии нормальное σn и касательное τnk напряжения на площадке (рис. 45), нормаль к которой повернута на угол
α по отношению к площадке, перпендикулярной оси x, определяются выражениями:
σn= σx cos2 α+ σz sin2 α |
|
τxz sin 2α, τnk = |
σx –2 |
σz |
sin 2α+ τxz cos 2α. |
|
|||||||||
Значения главных |
напряжений и положения главных площадок |
||||||||||||||
|
– |
|
|
|
|
|
|
|
|
|
|
|
|||
определяют выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
2 τxz |
|
||||
|
|
± σx – σz 2 + 4τxz2 , tg 2α = – |
|
||||||||||||
σ1,3 = |
|
σx + σz |
|
|
|
. |
|
||||||||
2 |
σx |
– |
σz |
|
|||||||||||
z |
50 |
|
|
|
|
|
|
|
z |
50 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30º |
|
|
|
|
|
|
|
|
100 |
x |
||
|
|
|
|
100 МПа x |
|
|
|
|
|
–30º |
|||||
|
|
|
|
|
|
k |
|
|
|
||||||
|
|
|
|
|
|
|
|
n |
|
||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
б |
|
|
|
|
Рис. 45. Схема плоского элемента, выделенного в твердом деформированном теле |
|
||||||||||||||
По условию, заданному на рис. 45, σx =100 МПа, σz = 0, τxz = 50 МПа.
Напряжения на наклонной площадке, повернутой на угол 30° и –30°, определяются выражениями соответственно:
25
σn = σx cos2 |
30° |
|
τxz sin 60° ; τnk = |
σx |
sin 60° + τxz cos 60° ; |
|||||||
|
2 |
|
||||||||||
|
|
σn = –σx cos2 |
|
|
|
|
|
|||||
|
|
30° τxz sin |
60° ; |
|||||||||
|
|
τnk = |
σx |
sin (– |
60°)–+ τxz cos (– |
60°) |
||||||
|
|
2 |
||||||||||
В первом случае |
σn = 31,7–МПа, τnk = 68,3– |
МПа.; во втором случае |
||||||||||
σn = 118,3 МПа, τnk = |
|
18,3 МПа. |
|
|
|
|
|
|
||||
Значения |
главных напряжений и положения главных площадок опреде- |
|||||||||||
|
– |
|
|
|
|
|
|
|
|
, tg 2α = –2 τxz⁄σx. |
||
ляются выражениями σ1,3 = 21 σx ± σx2 + 4τxz2 |
||||||||||||
Таким образом, σ1 = 122 МПа, σ3 = −22 Мпа, αn1 = –22,5°, αn2 = 112,5°.
Р.19. В примере, представленном на рис. 46, σx = 10 МПа, σz = 20 МПа, τxz = 0. Напряжения на площадках, нормаль к которым повернута
относительно оси x на углы 60° (рис. 46, а) и –60° (рис. 46, б), определим по формулам:
σn = σx cos2 α+ σz sin2 α, τnk = σx –2 σz sin 2α.
z |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
20 МПа |
|
|
||
20 МПа |
|
|
n |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
σn |
|
|
|
|
|
|
|
|
|
|
|
|
60º |
|
|
|
|
|
10 МПа |
|
|
|
|
|
10 МПа |
x |
|
|
|
−60º |
x |
||
|
|
|
|
|
k |
|
|||||
|
|
|
k |
|
|
|
|
σn |
|
||
|
|
|
τ |
|
|
|
|
|
|
||
|
|
|
|
nk |
|
|
|
τnk |
n |
|
|
|
|
|
|
|
|
|
|
|
|
||
а |
|
|
|
|
|
|
|
б |
|
|
|
Рис. 46. Схема плоского элемента, выделенного в твердом деформированном теле |
|
||||||||||
При повороте на угол 60°: |
|
|
|
|
|
|
|||||
σ |
= σ cos2 60° + σ |
sin2 60° = 17,5 МПа; |
|
|
|||||||
τnk = |
σnx –2 |
σx z |
sin 120° |
zσx –2 |
σz |
cos 30° ≈ 13 МПа |
. |
|
|||
При повороте на угол |
60°: |
|
|
–60° = 7,5 МПа; |
|
||||||
σn = σx cos–2 |
–60° |
+σz sin2 |
|
|
|||||||
26

τnk = |
σx –2 |
σz |
sin ( 120°) |
σx –2 |
σz |
cos 30° ≈ |
|
4,33 МПа. |
Р.20. Верхняя |
площадка (рис. 13, а) свободна от касательных |
|||||||
|
– |
|
|
– |
|
|||
напряжений. Главные напряжения на этой площадке равны нулю. Два других главных напряжения определим по формуле
σ |
1,3 |
= σ |
x |
+ σ ± |
σ |
x |
– σ |
2 + 4τ2 |
|
2 , tg 2α = 2τxz |
|
; |
|
|
|
|
z |
|
z |
xz |
|
– |
σx – σz |
|
|
||||
поскольку σx= σz = τxz = σ, σ1,3= |
2σ ± 2σ |
2 . |
|
|
||||||||||
В соответствии с правилом обозначения главных напряжений: σ |
1 |
= 2σ, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
⁄ |
|
|
||
σ2 = σ3 = 0. Напряженное состояние – линейное.
Боковая площадка (рис. 13, б) свободна от касательных напряжений. Главные напряжения на ней равны нулю. Два других главных напряжения определим по формулам: σx = σz = 0, σ1,3= ± τxz= ±100 МПа. Напряженное состояние – плоское.
Боковая площадка (рис. 13, в) свободна от касательных напряжений. Это одна из главных площадок, напряжение на которой равно 100 МПа.
Два других главных напряжения определим при следующих значениях нормальных и касательных напряжений на площадках: σx= σz = τxz = = 100 МПа.
Одно из главных напряжений равно 200 МПа, а другое равно нулю. В соответствии с правилом обозначения главных напряжений σ1 = 200 МПа, σ2 = 100 МПа, σ3 = 0. Напряженное состояние – плоское.
Р.21. Эпюры напряжений в поперечном сечении стержня в окрестностях точек А, В, С имеют вид, показанный на рис. 47, б.
В окрестностях точек выделим элементарные параллелепипеды, на гранях которых представим напряжения в окрестностях точек: А (рис. 47, в), В (рис. 47, г), С (рис. 47, д). Одна из граней каждого параллелепипеда совпадает с поперечным сечением.
Точка А (рис. 47, в). Все три грани элементарного параллелепипеда являются главными площадками. На двух гранях напряжения равны нулю, на третьей напряжение отлично от нуля: σ1 = σx A, σ2 = σ3 = 0. Напряженное состояние – линейное. σx A – значение нормального напряжения в точке А.
Точка В (рис. 47, г). Напряжения на боковой грани равны нулю. Это одна главная площадка. Напряжения на двух других главных площадках
27
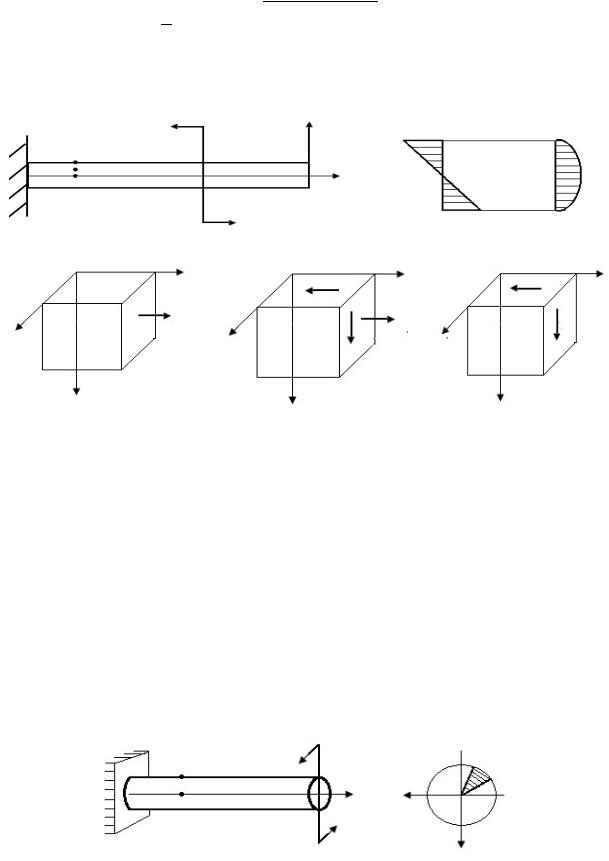
σ1 = |
1 |
σx B + σx 2+ 4 τxz2 B ; σ3 = – τxz B, |
2 |
где σx B, τxz B – значения нормального и касательного напряжений в окрестности точки В.
M |
|
P |
σ |
x |
τxz |
|
|
|
|||
|
|
|
|
|
|
A |
|
|
|
|
|
B |
|
|
|
|
|
C |
|
x |
|
|
|
|
|
|
|
|
|
а |
|
|
|
б |
|
x |
|
τzx |
x |
τzx |
x |
σx |
y |
τxz |
σx |
y |
τxz |
y |
|
||||
|
|
|
|||
z |
|
z |
|
z |
|
в |
|
г |
|
д |
|
Рис. 47. Схема нагруженного стержня (а), эпюры нормального и касательного напряжений (б), схемы прямоугольных
параллелепипедов, вырезанных из нагруженного стержня (в–д)
Точка С (рис. 47, д). Напряжения на боковой грани равны нулю. Это одна главная площадка. Напряжения на двух других гранях равны:
σmax = τxz C, σmin = – τxz C,
где τxz C – значение касательного напряжения в окрестности точки С. Таким
образом, σ1 = τxz C, σ2 = 0, σ3 = – τxz C. Напряженное состояние – плоское. Р.22. В окрестности точек А, С (рис. 48) выделим элементарные
параллелепипеды. Одна из граней каждого параллелепипеда совпадает с поперечным сечением.
A |
M |
|
τx |
|
|
||
|
|
|
|
C |
x |
y |
C |
|
|
|
z |
а |
|
|
б |
Рис. 48. Схема нагруженного стержня (а) и эпюр касательных напряжений (б)
28
|
|
Точка С. Напряжения в окрестности |
|
точки |
С |
σ1 = σ2 = σ3 = 0. |
||||||||||||||
Напряженное состояние – нулевое. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Точка А. Напряженное состояние в точке А определим при рассмотрении |
||||||||||||||||||
кубического |
уравнения. |
Учитывая, что |
Θ |
I |
= Θ |
III |
= 0, Θ |
= τ2 |
+ τ2 |
= τ2, |
||||||||||
|
|
|
|
|
|
|
|
– |
|
|
|
|
– |
|
II |
xy |
xz |
x |
||
кубическое уравнение принимает вид σ3 |
τx2σ = σ |
σ2 |
τx2 |
= 0, получаем: |
||||||||||||||||
σ |
2 |
= 0, |
σ |
1,3 = ± τx A, где |
τx A – |
|
|
τ |
x |
в |
|
|
|
|
|
точки А. |
||||
|
|
|
|
|
значение |
|
окрестности |
|||||||||||||
Напряженное состояние – плоское. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Р.23. |
На |
гранях представлены |
главные |
напряжения. |
Эквивалентное |
|||||||||||||
напряжение σэкв по четвертой теории прочности определяют по следующей
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
формуле: σэкв= σ1 |
|
σ2 |
2+ σ2 |
σ3 |
2+ σ3 |
|
|
σ1 |
2 2 . |
|
|
||||||
В окрестности |
точки (рис. 16) действуют главные напряжения |
σ1 |
= σ, |
||||||||||||||
|
– |
|
– |
|
|
– |
|
|
|
|
|||||||
σ2 = 0, σ3 = |
σ. В результате получим σэкв = |
|
|
|
|
|
|
|
|||||||||
|
|
3σ |
|
|
|
|
|||||||||||
Р.24. |
На |
гранях представлены главные напряжения. Эквивалентные |
|||||||||||||||
– |
|
|
|
|
|
|
|
|
|
√ . |
|
|
|||||
напряжения по теории наибольших касательных напряжений определяются
по формуле σ |
экв=σσ1–=σ3, |
а по |
четвертой теории прочности по формуле |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
σ |
|
σ |
2 |
2+ σ |
2 |
|
σ |
3 |
2+ σ |
3 |
|
σ |
1 |
2 |
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
экв |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0, |
σ |
|
||||||||
|
|
|
|
|
|
|
|
следующие главные напряжения: а) σ |
|
|
||||||||||||||||||||
σ3 |
= |
На гранях действуют |
|
|
– |
|
|
|
|
– |
|
|
|
|
– |
|
σ. |
|
|
. |
1 |
|
|
|
2 |
|||||
– |
σ; б) σ1 = σ2 = σ, σ3 |
|
= 0; в) σ1 = σ, σ2 = 0, σ3 |
= |
– |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
При расчете по четвертой теории прочности для напряженных |
|||||||||||||||||||||||||||
состояний случаев а, б, в |
|
напряжения σэкв соответственно равны |
|
σ 2, |
||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||
|
|
σ 2, 2σ. Самое неблагоприятное напряженное состояние – в случае в√. |
|
|
/ |
|||||||||||||||||||||||||
|
2 |
|
|
|||||||||||||||||||||||||||
√ |
/При расчете по теории наибольших касательных напряжений для напря- |
|||||||||||||||||||||||||||||
женных состояний а, б, в напряжения σэкв соответственно равны σ, σ, 2σ. Самое неблагоприятное напряженное состояние – случай в.
|
Р.25. На гранях представлены главные напряжения σ1 = 300 МПа, |
|||
σ = 200 МПа σ = |
100 МПа. По теории наибольших касательных напряже- |
|||
ний2 |
эквивалентное, 3 –напряжение, определяемое |
по формуле |
σэкв= σ1 σ3, |
|
равно 400 МПа. |
Это напряжение превышает |
допускаемое |
напряжение |
|
– |
||||
σ = 250 МПа. Деформируемое тело не удовлетворяет условиям прочности. Р.26. На гранях представлены главные напряжения σ1 = σ, σ2 = 0,
σ3 = – σ. Главные деформации определяются по формулам:
29
ε1 = |
1 |
|
σ1 ν σ2 + σ3 ; ε2 = |
|
1 |
|
σ2 |
|
|
ν σ1+ σ3 ; ε3 |
= |
1 |
|
|
σ3 ν σ1+ σ2 . |
|
|
|||||||||||||||||||||||||||||||||||||
E |
|
E |
|
|
E |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Главные–линейные деформации |
соответственно равны: |
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ε1 |
= |
1 |
σ + νσ ; ε2 |
|
= 0; ε3 |
= |
|
|
1 |
|
σ + νσ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
E |
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= σ |
|
|
+ σ |
|
|
+ σ |
|
|
не зависит |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
напряжений Θ |
|
|
|
|
|
||||||||||||||||||||||||||
|
Р.27. Первый инвариант тензора |
|
|
|
|
|
– |
|
|
I |
|
|
x |
|
|
|
y |
|
|
|
z |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
от |
пространственной |
|
ориентации |
|
|
параллелепипеда. |
|
|
|
Следовательно, |
||||||||||||||||||||||||||||||||||||||||||||
σx+ σy+ σz= 700 МПа, σx1+ σy1 = 350 МПа и, значит, σz1 = 350 МПа. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Р.28. Сумма относительных удлинений не зависит от пространственной |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
ориентации элементарного параллелепипеда. Так как ε |
|
|
+ ε |
|
|
+ ε |
|
|
= 0,03 |
|
, а |
|||||||||||||||||||||||||||||||||||||||||||
εx1 + εy1= 0,022, то εz1 = 0,008. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|
|
z |
|
|
|
|
|
0 |
|
||||||||||||||||||
|
Р.29. Стержень, показанный |
|
|
|
|
на рис. 19, испытывает нормальное |
||||||||||||||||||||||||||||||||||||||||||||||||
напряжение σ = N F, N = P, F = π ((2r)2 |
– |
r2) = 3πr2 |
, где N – нормальная сила, |
|||||||||||||||||||||||||||||||||||||||||||||||||||
F – |
площадь |
|
|
⁄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
поперечного сечения стержня. Относительное продольное |
||||||||||||||||||||||||||||||||||||||||||||||
удлинение |
стержня |
|
ε1 = |
|
|
= /(3Eπr2), |
где E |
– модуль |
|
нормальной |
||||||||||||||||||||||||||||||||||||||||||||
упругости |
|
материала |
стержня. Относительное поперечное удлинение |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
σ/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
νP /(3Eπr2). |
|||||||||||||||||||||
стержня |
ε2 = |
|
|
νε1, |
|
где ν |
– |
|
коэффициент |
|
Пуассона. |
|
|
ε2 = |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
радиуса стержня |
r = ε |
r = |
|
|
νP/(3Eπr). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Изменение |
|
– |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
||||||||||
|
Р.30. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определяется по формуле ν = |
|
|
|
|
|
|
||||||||||||||||||||||||||||
где |
ε |
|
|
|
Коэффициент Пуассона |
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
ε1 |
|
||||||||||||||
1= |
|
l |
l = 0,04 |
20 =0,002 |
– |
νотносительное |
продольное |
|
|
удлинение |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
– |
|
|
⁄ |
|
, |
|||||||||||||||||||||||||||||||||||||||||||
стержня; |
|
⁄ε2 = |
|
r r⁄= |
|
|
0,0016 |
2 = |
|
|
|
|
0,0008 |
– |
|
относительное |
поперечное |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Коэффициент Пуассона равен ν = 0,0008 |
0,002 = 0,4. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
сужение стержня. ⁄ |
|
– |
|
|
⁄ |
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
⁄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Расчет напряжений и анализ прочности стержней
Р.31. На стержнях, показанных на рис. 20, нумерацию грузовых участков будем проводить слева направо.
Из условия статического равновесия стержня (рис. 20, а) нормальные силы на первом и втором участках соответственно равны: N1 = P, N2 = 5P.
Нормальное напряжение σx1 = P/a2 , σx2 = 5P/4a2. Максимальное напряжение наблюдается на втором участке.
Нормальные силы и нормальное напряжение в стержне, представленном на рис. 20, б, равны N1 = 6P, N2 = 5P, N3 = 5P; σx1 = 6P/9a2, σx2 = 5P/4a2,
σx3 = 4P/a2. Максимальное напряжение – на третьем участке.
30
