7.3 Декодирование циклического кода
1. Способы декодирования с обнаружением ошибок
Процедура декодирования циклического кода с обнаружением ошибок, по аналогии с процессом кодирования, использует два способа:
- при кодировании "классическим" способом декодирование основано на использовании свойства делимости без остатка кодового многочлена F(x) циклического (n,m)-кода на порождающий многочлен g(x). Поэтому алгоритм декодирования включает в себя деление принятого кодового слова, описываемого многочленом F(x) на g(x), вычисление и анализ остатка R(x). Если R(x)=0, то принятое кодовое слово считается неискаженным. Если R(x)0, то принятое кодовое слово стирается и формируется сигнал "ошибка".
- при кодировании
способом МККТТ декодирование основано
на свойстве получения определенного
контрольного остатка R0(x)
при делении принятого кодового многочлена
F(x)
на порождающий многочлен g(x).
Поэтому, если полученный при делении
остаток
=R0(x),
то принятое кодовое слово считается
неискаженным. Если остаток
R0(x),
то принятое кодовое слово стирается и
формируется сигнал "ошибка".
Значение контрольного остатка определяется
из выражения R0(x)=Rg(x)
x(1)r-1
xk.
2 Способы декодирования с исправлением ошибок
Декодирование заключается в определении номера искаженного разряда и его автоматического исправления. А также отделения информационных разрядов от контрольных.
Рассмотрим три методики декодирования
Определение искаженного разряда с помощью матрицы ошибок.
Если ошибок нет, то остаток от деления равен нулю
.
Матрица одиночных ошибок имеет вид
где
-
единичная матрица;
- прямоугольная проверочная матрица.
Строки матрицы определяются из выражений
- остаток от деления
на образующий полином
,
где - значение i-той строки матрицы ;
i - номер строки матрицы .
Пример. Матрица для (7,4)-кода на основе порождающего многочлена имеет вид
.
Единичная матрица размерности 7х7
.
Рассчитаем проверочную матрицу
при
.
Определим остаток от деления на образующий полином .
.
При
.
Определим остаток от деления на образующий полином .
.
При
.
Определим остаток от деления на образующий полином .
111.
При
.
101.
При
.
100.
При
.
010.
При
.
001.
Тогда матрица ошибок
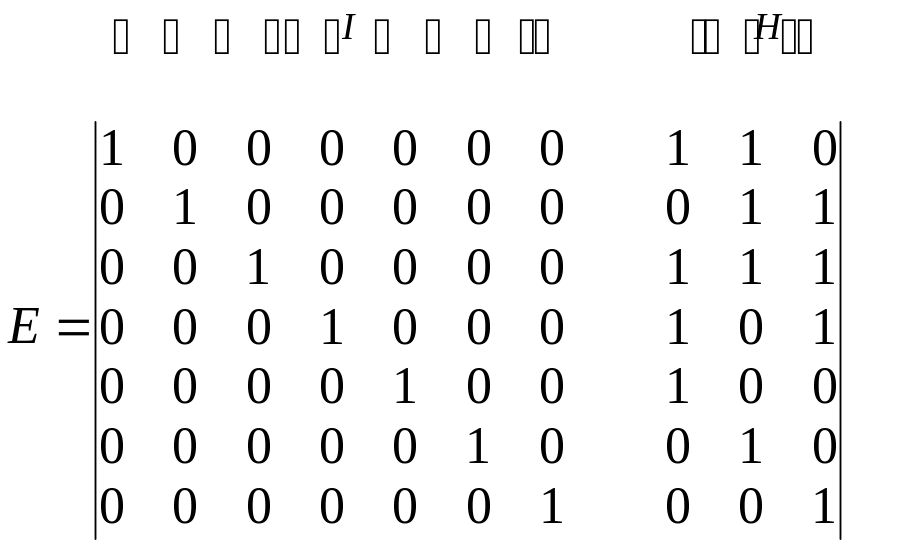
Для определения
искаженного разряда необходимо определить
остаток от деления принятой кодовой
комбинации
на порождающий многочлен
.
Пример
Внесем искажения
Находим остаток
1 0 1 0 1 0 0 |
|
1 1 0 1 |
|
1 1 1 1 |
|
1 1 0 1 |
|
0 0 1 0 0 0 |
|
1 1 0 1 |
|
1 0 1 |
- остаток |
Н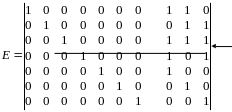
аходим
строку в матрице ошибок с полученным
остатком
Искаженный разряд – это разряд в данной строке в которой стоит «1».
Искаженный разряд исправляем посредством сложения строки в матрице ошибок полученной комбинации
.