Лекция 6 блочные линейные коды

6.1 Математическое описание процессов кодирования и декодирования

6.2 Коды с проверкой на четность

6.3 Коды Хэмминга

6.4 Коды с постоянным весом

6.1 Математическое описание процессов кодирования и декодирования

Линейным блочным - кодом называется множество последовательностей длины над , называемых кодовыми словами, которое характеризуется тем, что сумма двух кодовых слов является кодовым словом, а произведение любого кодового слова на элемент поля также является кодовым словом.

Поле , состоящее из конечного числа элементов называется конечным полем или полем Галуа. Для любого числа , являющегося степенью простого числа, существует поле, насчитывающее элементов. Поле не может содержать менее двух элементов, поскольку в нем должны быть, по крайней мер,е единичный элемент относительно операции сложения (0) и единичный элемент относительно операции умножения (1). Поле, включающее только 0 и 1, обозначим GF(2). Правила сложения и умножения в поле с двумя элементами следующие:

+	0	1		х	0	1
0	0	1		0	0	0
1	1	0		1	0	1

Двоичные кодовые комбинации, являющиеся упорядоченными последовательностями из элементов поля , рассматриваются в теории кодирования как частный случай последовательностей из n элементов поля .

Обычно , где - некоторое целое число. Если , линейные коды называются групповыми, так как кодовые слова образуют математическую структуру, называемую группой. При формировании этого кода линейной операцией является суммирование по mod2.

При задании кода обычно указывают, какие информационные элементы принимают участие в формировании каждого из k проверочных разрядов. Например, для кода с n=5, m=3 и k=2 каждый проверочный разряд определяется суммированием по модулю 2 по правилу

;

где - информационные разряды. Комбинация такого кода записывается в виде или в обратном . При задании кода можно указать все разрешенные для этого кода комбинации. Для линейных кодов способ задания можно значительно упростить. Для m информационных разрядов число всех разрешенных кодовых комбинаций будет равняться .

Пусть . Так как в каждой кодовой комбинации такого кода три информационных элемента, то число возможных комбинаций кода будет равно , а именно:

Таблица 6.1

№ п/п	а1	а2	а3	b1	b2
1 2 3 4 5 6 7 8	1 0 0 1 0 1 1 0	0 1 0 1 I 0 1 0	0 0 1 0 I 1 1 0	1 1 0 0 I 1 0 0	0 1 1 1 0 1 0 0

проверочные символы

информационные

символы

(элемнта)

Проверочные элементы формируются как сумма по модулю два информационных элементов, а именно:

(6.1)

Так для кодовой комбинации №4

в соответствии с правилами суммирования по модулю 2. Знак означает суммирование по модулю.

Минимальный вес кодовой комбинации представляет число разрядов, в которых элементы являются единичными. Для рассматриваемого кода =2. То есть каждая кодовая комбинация содержит не менее двух единиц.

Для задания кода нет необходимости записывать в таблицу все используемые комбинации данного кода. Код может быть задан матрицей, которая содержит один из возможных наборов линейно независимых строк. Линейно независимыми называют такие строки, любая комбинация суммирования которых по модулю 2 не дает нулевых комбинаций.

Или

Обычно линейно независимые кодовые комбинации записывают в виде матрицы размером , которая называется порождающей (или производящей) и обозначается . Чаще всего порождающие матрицы записывают в так называемой каноничной форме. При этом первые или последние столбцов этой матрицы образуют единичную матрицу.

Таким образом, любая из трех приведенных выше комбинаций может быть порождающей для систематического (5,3) кода с d_min=2. В общем виде производящую матрицу из строк и – столбцов записывают так:

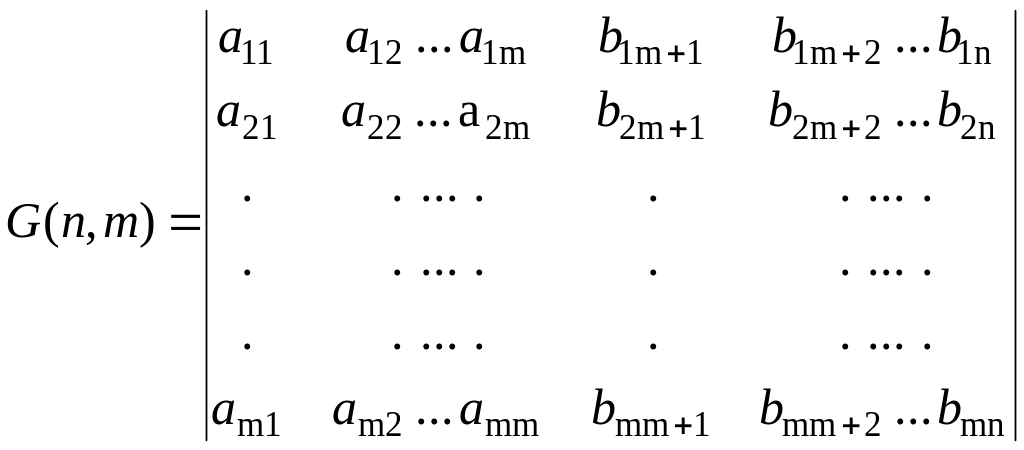. (6.2)

Здесь первые столбцов являются информационными и последние столбцов – проверочными. Производящую матрицу обычно записывают в канонической форме

или . (6.3)

где – число проверочных элементов, - матрица информационных элементов, представляет собой единичную матрицу размерности , т.е. квадратная матрица, у которой единицы находятся только на главной диагонали, - матрица проверочных элементов, размерность которой .

Для рассматриваемого примера – (5,3) кода каноническая форма порождающей матрицы имеет вид

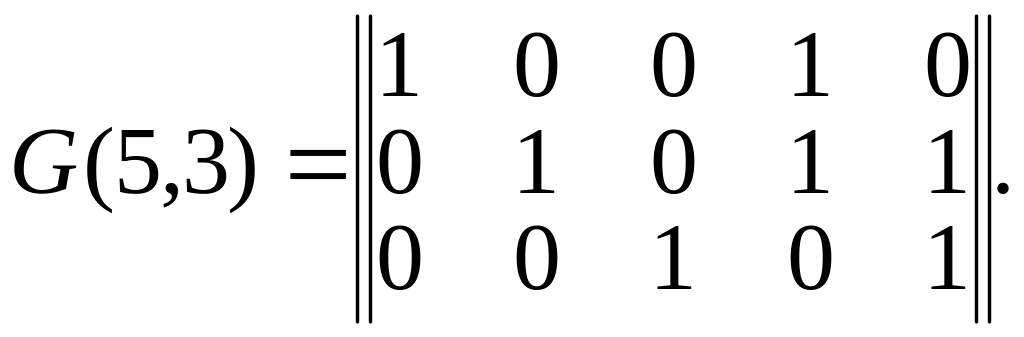
Из данного примера видно, что первые три столбца составляют единичную матрицу; четвертый столбец указывает, что при формировании первого проверочного разряда принимают участие первый и второй информационные разряды. Пятый столбец указывает, что при формировании второго проверочного разряда принимают участие второй и третий информационные разряды.

Для

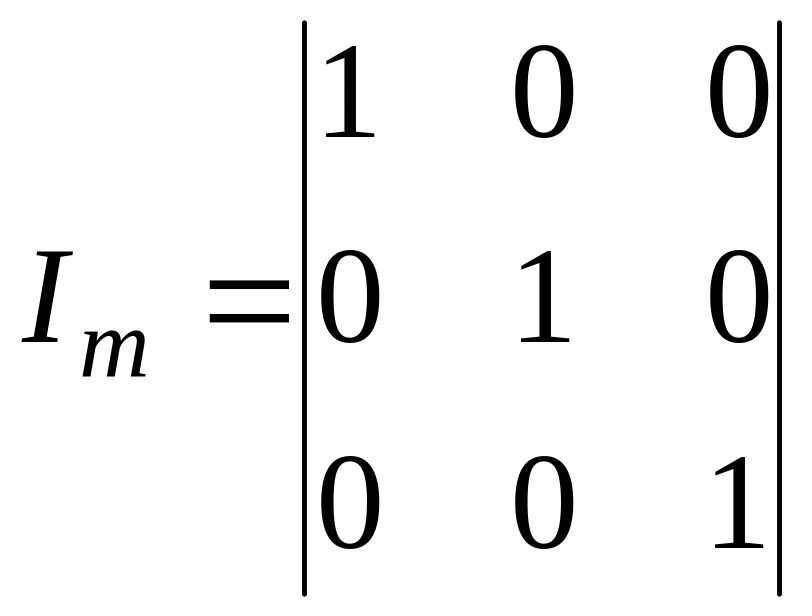. (6.4)

Затем выделяется подматрица являющаяся транспонированной матрицей :

если 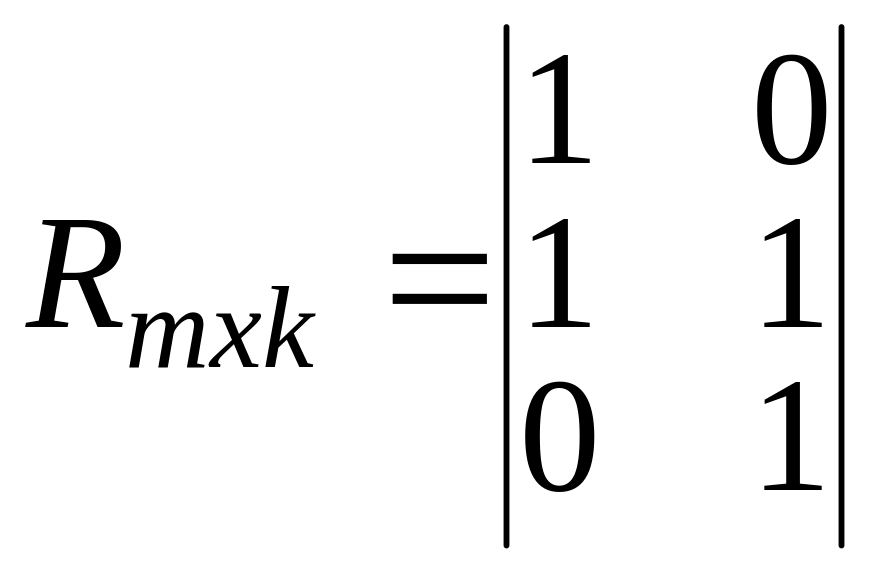то . (6.5)

Затем полученной матрице справа приписывается единичная матрица и получается проверочная матрица Н.

. (6.6)

Проверочная матрица очень удобна для определения места ошибки в кодовой комбинации, а следовательно и исправления ошибки.

Проверочная матрица однозначно связана с порождающей соотношением

, (6.7)

Где умножение и суммирование соответствующих элементов матриц производится по модулю 2. Напомним, что умножение по модулю 2 представляется в виде , , .

Пример.

Для порождающей матрицы, G(5,3) проверочная матрица имеет вид

Тогда

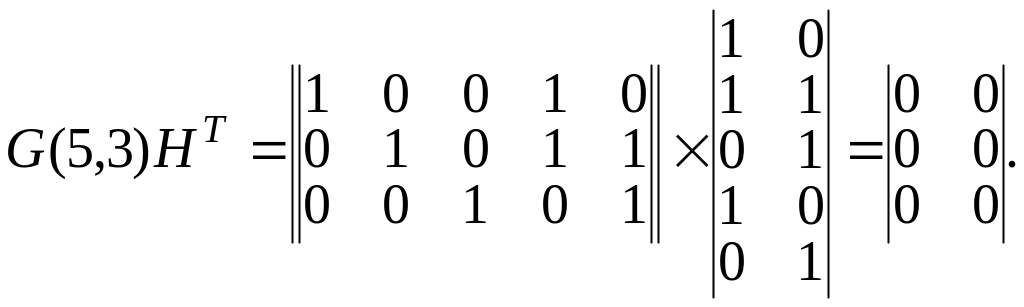
Допустим, что переданная кодовая комбинация записана в виде вектора

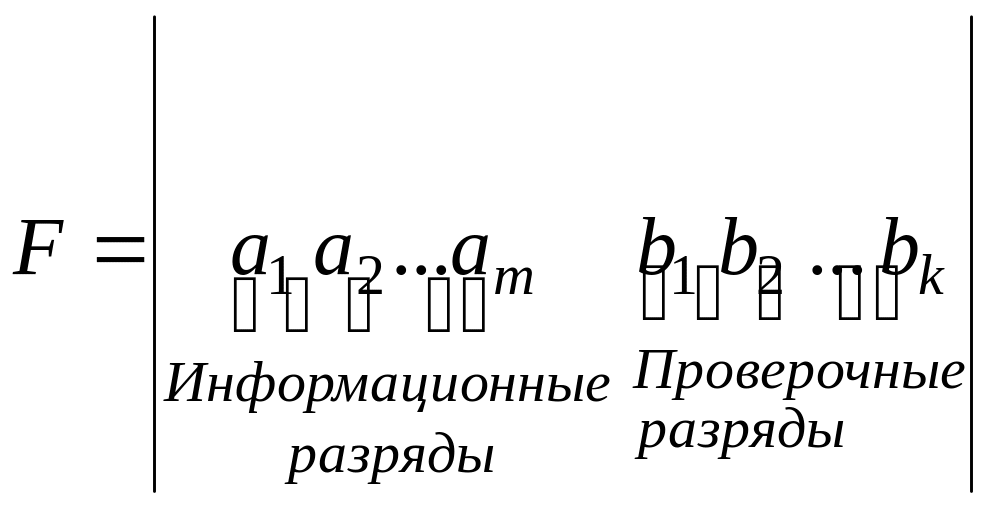(6.8)

Процесс декодирования математически описывают произведением проверочной матрицы и вектора – столбца, отображающего принятую кодовую комбинацию , где - вектор ошибки

(6.9)

где – результат декодирования (синдром);

- знак транспортирования.

В теории кодирования синдром, который также называют опознавателем ошибки, обозначает совокупность признаков, характерных для определённой ошибки.

Пример.

Передается комбинация

.

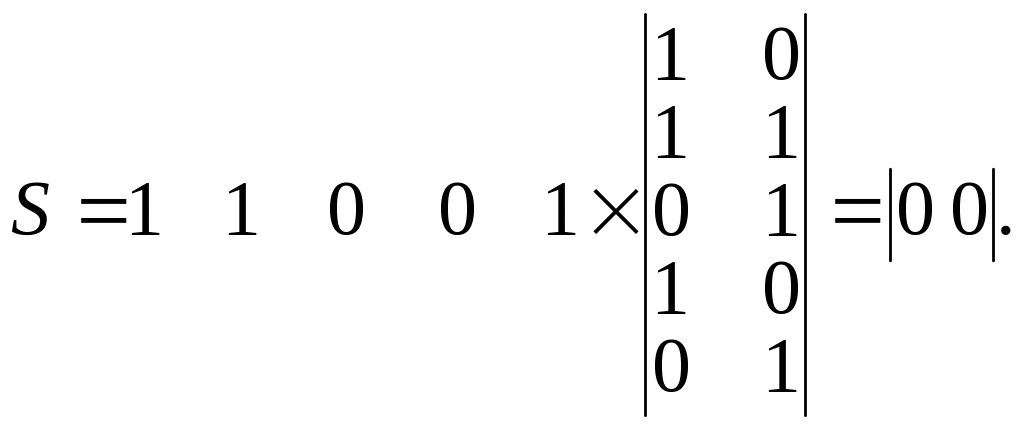
Ошибки нет.

Под воздействием помех

.

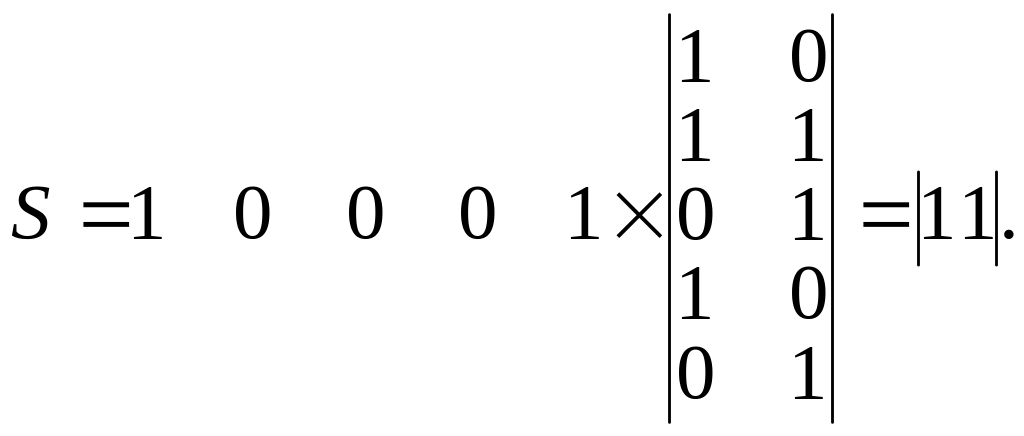
Ошибка обнаружена.

Для исправления ошибки на стороне приёма необходимо знать не только факт её существования, но и её местонахождение, которое определяется по установленному виду вектора ошибки.

Поскольку связь между порождающей и проверочной матрицами, определяется равенством , то получим

. (6.10)

Если обозначить - й столбец проверочной матрицы, то

.

Вектор ошибки содержит «1» на тех позициях, символы на которых искажены. Пусть эти позиции имеют номера , тогда будет справедливо равенство

. (6.11)

Следовательно, если необходимо обнаружить ошибок, то должно быть выполнено условие

,

при любом сочетании искаженных символов.

Если же необходимо исправить ошибок, то сумма по модулю 2 для любого конкретных столбцов проверочной матрицы должна быть вполне определенной, которая не совпадает с аналогичной суммой для других столбцов. Так, например, при исправлении одиночной ошибки все столбцы проверочной матрицы должны быть разными, то есть при любых и ; . Если же необходимо исправить одиночную ошибку и обнаружить пакет, состоящий из трех или двух ошибок, то необходимо выполнить следующие условия:

при (для исправления одиночной ошибки);

при любых и (для обнаружения пакета из двух ошибок);

при любых и (для обнаружения пакета из трех ошибок).

Матрицы и можно поменять ролями. Тогда матрица будет порождающей, а - проверочной.

Коды, взаимосвязанные между собой таким образом, называют дуэльными (двойственными).