519_8_E92_2015_Efromeeva_E_V__Efromeev_N_M_Metody_issledovania_operatsiy_v_mashinostroenii_primery_zadachi_2-e_izdanie

Отсюда следует, что полученное методом наименьшей стоимости начальное решение, представленное методом северо-западного угла, хуже, чем методом минимального элемента (сравните данное значение целевой функции с аналогичным значением из п. 7.6.1).

7.6.3. Метод Фогеля

Данный метод является вариацией метода минимального элемента и в общем случае находит лучшее начальное решение. Алгоритм этого метода состоит из следующих шагов.

Шаг 1. Для каждой строки (столбца), которой соответствует строго положительное предложение (спрос), вычисляют штраф путем вычитания наименьшей стоимости из следующей по величине стоимости в данной строке (столбце).

Шаг 2. Выделяют строку или столбец с наибольшим штрафом. Если таковых несколько, выбор произволен. Из выделенной строки или столбца выбирают переменную, которой соответствует минимальная стоимость, и ей присваивают наибольшее значение, позволяемое ограничениями. Затем в соответствии с присвоенным значением переменной корректируются величины оставшегося неудовлетворенным спроса и нереализованного предложения.

111

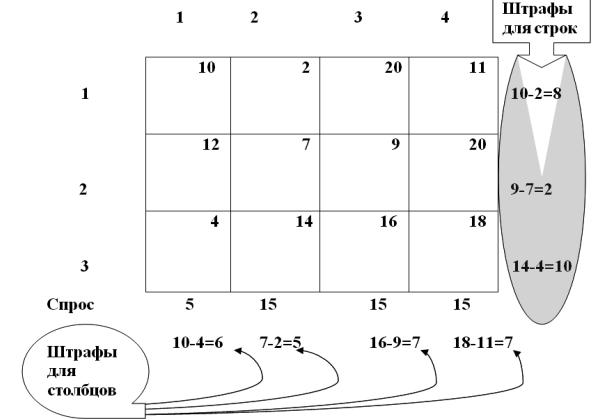
Строку (или столбец), соответствующую выполненному ограничению, вычеркивают из таблицы. Если одновременно выполняются ограничения и по спросу, и по предложению, вычеркивают только строку или только столбец, причем оставшейся строке (столбцу) приписывают нулевое предложение (спрос).

Шаг 3.

а) если не вычеркнута только одна строка или только один столбец с нулевым спросом или предложением, вычисления заканчивают.

б) если не вычеркнута только одна строка (столбец) с положительным предложением (спросом), в этой строке (столбце) методом наименьшей стоимости находятся базисные переменные, и вычисления заканчивают.

в) если всем невычеркнутым строкам и столбцам соответствуют нулевые объемы предложения и спроса, методом минимального элемента находят нулевые базисные переменные, и вычисления заканчивают.

г) во всех остальных случаях необходимо перейти к п. 1.

Применим метод Фогеля к задаче. В приведенной ниже таблице показан первый набор вычисленных штрафов.

112

Поскольку третья строка имеет наибольший штраф (10) и в этой строке наименьшая стоимость содержится в ячейке (3, 1), присваиваем переменной x31 значение 5. В этом случае полностью выполняется ограничение первого столбца, его вычеркиваем. Новый набор показан в следующей таблице.

Теперь первая строка имеет наибольший штраф 9. Поэтому мы присваиваем значение 15 переменной •••, которой соответствует минимальная стоимость в первой строке. В этом случае одновременно выполняются ограничения и для первой строки, и для второго столбца. Вычеркиваем второй столбец, приняв объем предложений, соответствующий первой строке, равным

нулю.

20 − !•"

присваиваем значение 15. В результате будет вычеркнут третий столбец, во второй строке останется нереализованным предложение объемом в 10 единиц. Остается невычеркнутым только четвертый столбец с положительным неудовлетворенным спросом объемом в 15 единиц! 0. !Применяя10 ! метод5. минимального элемента, последовательно получаем •# = , •# = , "# =

Соответствующее значение целевой функции равно

%= 15 ∙ 2 + 0 ∙ 11 + 15 ∙ 9 + 10 ∙ 20 + 5 ∙ 4 + 5 ∙ 18 = 475.

Вданном случае значение целевой функции такое же, как при методе минимального элемента. Но обычно метод Фогеля дает наилучшее начальное решение для транспортной задачи.

113

7.7. Решение транспортной задачи методом потенциалов

Для нахождения оптимального плана перевозок необходимо уметь оценивать полученный план на оптимальность. Как это сделать, не имея в распоряжении всех возможных планов перевозок, которые можно было бы сравнить между собой? Для оценки плана на оптимальность вводится понятие косвенных затрат. Косвенные затраты - это затраты, получаемые для маршрутов, по которым не осуществляются перевозки при данном плане. Рассчитанные косвенные затраты сравнивают с реальными затратами, которые имели бы место, при условии, что перевозки осуществлялись по данным маршрутам. Если для всех невыбранных маршрутов косвенные затраты не больше реальных, то данный план перевозок является оптимальным. Если хотя бы для одного маршрута косвенные затраты больше реальных, то план перевозок может быть улучшен введением в него данного маршрута. Ввод нового маршрута в план перевозок соответствует вводу в список базисных переменных переменной транспортной задачи, соответствующей этому маршруту. Эти рассуждения лежат в основе ряда методов, применяемых для нахождения оптимального плана перевозок.

Рассмотрим один из них - метод потенциалов. В соответствии c этим методом критерий оптимальности плана формулируется следующим образом.

Допустимый план перевозок тогда и только тогда является оптимальным, когда каждому пункту отправления и назначения можно сопоставить величину, характеризующую уровень оценки груза в нем (потенциал) так, что множество этих потенциалов удовлетворяет следующим условиям:

1.Разность потенциалов пунктов назначения и отправления, между которыми запланированы перевозки, равна затратам по транспортировке единицы груза между этими пунктами.

2.Аналогичные разности для всех остальных пар пунктов, между которыми не запланированы перевозки, не превосходят затрат по транспортировке.

Иначе говоря, если обозначить через • потенциал для i-го пункта отправления, а через !" - для j-го пункта назначения, то эти условия

записывают так:

!" + • ≤ $ " ,

причем !" + • = $ ", если перевозка из пункта % в пункт &" предусмотрена в плане (' " > 0).

В транспортной задаче оценки (потенциалы) имеют прозрачный экономический смысл. Они выступают здесь как локальные (поясные) цены (или наценки к единой цене), создающие заинтересованность в правильном направлении перевозок. При такой интерпретации признак оптимальности плана представляет собой по сути математическое выражение здравого смысла: если какая-то перевозка осуществляется, то цена в пункте потребления равна цене в пункте производства плюс транспортные затраты; в остальных случаях

114

цена •• не может быть больше, чем !• − #!, так как продукт в пункте $• по такой цене можно было бы получить, привезя его с затратами %• из пункта &!. Следовательно, %• ≤ !• − #!, т.е. в обоих указанных случаях разность цен не превышает затрат по перевозке.

С помощью критерия оптимальности можно не только проверить на оптимальность любой план, но и в случае его неоптимальности, указать способ улучшения этого плана. Приведем пример построения оптимального плана с помощью последовательного улучшения, исходя из некоторого исходного допустимого плана, например, приведенного в таблице опорного плана.

Для того чтобы проверить план таблицы на оптимальность, прежде всего вычисляем систему потенциалов (оценок единицы продукта) в пунктах отправления и пунктах назначения. Так как потенциалы определяют c точностью до постоянного слагаемого (важно соотношение между потенциалами, а не их абсолютная величина), то значение какому-нибудь из них можем присвоить заранее. Пусть, например, #( = 10 (обычно #( полагают равным нулю), причем через # обозначим потенциалы пунктов отправления, а через % - назначения. Используя тот факт, что разность потенциалов между пунктами назначения и отправления, связанными в плане перевозками, равны соответствующим транспортным затратам, один за другим находим остальные потенциалы:

Теперь проверим выполнение признака оптимальности. Для этого нужно согласно условию 2 подсчитать величины %• + #! − !•. Если они вcе ≤ 0, то план оптимален, иначе план может быть улучшен.

Находим:

Для пунктов, между которыми предусмотрены перевозки, эти разности, очевидно, равны нулю и поэтому их не будем выписывать. Так как некоторые из найденных значений разностей положительны, то план не оптимален. Чтобы его улучшить, введем в план перевозку в объеме K между пунктами А4 и В2, для которых соответствующая разность положительна и максимальна по величине. Однако введение добавочной перевозки нарушает сбалансированность плана (объем ввоза в пункт •, не соответствует его заявке

одновременно изменить объемы перевозок и между некоторыми другими

Нетрудно проверить, что этот план сбалансирован - из каждого пункта вывозится столько, сколько в нем запасено, а каждый пункт назначения получает столько, какова его заявка.

Легко убедиться, что затраты по реализации этого плана перевозок меньше первоначальных на величину (V2-U4-C42)K=3K. Действительно, эти затраты равны

L=(11-K)C11+(22+K)C13+15C14+4C21+26C25+(3+K)C31+(24-K)C32+KC42+

+(20-K)C43=Lпп-(C11-C13+C32-C31+C43-C42)K,

где Lпп - стоимость прежнего плана. С другой стороны, из соотношений

V2=U3+C32, U3= V1-C31, V1= U1+C11, U4= V3-C43, V3= U1+C13 следует, что

(V2-U4-C42) =C11-C13+C32-C31+C43-c42. Это и доказывает вышеприведенное утверждение.

Следовательно, выгодно К выбрать, как можно большим. Поскольку объемы перевозок не могут быть отрицательными, наибольшее возможное значение К равно 11. Полагая К=11, находим новый допустимый и опорный план. Он экономически является более выгодным планом. Этот план приведен в таблице.

Нахождением нового опорного плана заканчивается первое приближение. Дальше проведенные операции повторяют снова, но уже для нового плана. Прежде всего вычисляют потенциалы и проверяют условия оптимальности. Если они выполнены, то решение закончено. Если нет, то снова переходят к лучшему плану и т.д.

7.8.Случаи вырождения и способы их преодоления

•+Выше− 1отмечалось, что число занятых мест в таблице должно быть равно

. Однако на практике встречаются случаи, когда в процессе решения

оно сокращается. Это явление называется вырождением. Рассмотрим данный случай на конкретном примере. В таблице имеется свободное место - ячейка (1,2). Воспользуемся им для улучшения решения.

При вычитании 50 из клеток (2,2) и (1,3) значения их превращаются в 0. В результате сокращается число занятых клеток и невозможно воспользоваться методом потенциалов.

Для преодоления этого в одну из освободившихся клеток поставим 0 и

•будем+ • −считать1 эту клетку занятой. Число занятых мест в таблице равно 6 (т.е.

).

Иногда приходится встречаться с вырожденным случаем уже при составлении исходного решения. Вырождения в этом случае можно избежать, переставляя местами столбцы или строки.

117

7.9. Транспортные задачи с дополнительными ограничениями

Пусть требуется при решении транспортной задачи ограничить перевозки

7.9.1. Задачи с обязательными поставками

Необходимо прежде, чем решать задачу, сократить (уменьшить) запасы -

Пусть в силу определенных обстоятельств (например, госзаказ) третий поставщик А3, несмотря на фактические затраты, обязан поставить четвертому потребителю В4 не менее 100 единиц продукции. Исключим эту обязательную поставку из транспортной таблицы

Затем решается обычная транспортная задача, но при определении суммарных затрат на перевозки необходимо учесть и затраты на обязательные

поставки: 100×52=5200.

7.9.2.Задачи с запретами

Вряде случаев поставки по некоторым каналам оказываются недопустимыми. Это, например, могут быть условия технологии (предприятии, производящее продукцию на экспорт не может потреблять сырье низкого качества), отсутствие у потребителя подходящей взлетно-посадочной полосы для приема воздушных транспортных средств и пр.

Втаком случае в соответствующую клетку• транспортной таблицы вместо реальной стоимости перевозки ставится (сколь угодно большое число,

большее любого наперед заданного числа). Далее задача решается методом потенциалов.

7.9.3. Задачи с ограниченной пропускной способностью

Пусть в силу некоторых обстоятельств по каналу А! − В$ можно поставить не более % единиц продукции.

Представим поставщика А! в виде двух поставщиков – &'! и &(!, находящихся в одном и том же месте. Производственные мощности этих поставщиков соответственно )! − % (ограничение на поставку) и % единиц. Естественно, что затраты на перевозки у &'! и &(! останутся такими же, как и у А!, однако для выполнения поставленного ограничения у поставщика &'! по каналу &'! − В$ поставим запрет М.

7.10. Транспортная задача по критерию времени

Задача по критерию времени возникает при перевозке срочных грузов. Как и в обычной транспортной задаче, имеется * поставщиков с запасами

Требуется составить такой план перевозок груза, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и наибольшее время доставки всех грузов является минимальным.

Составим математическую модель этой задачи. Обозначим ••• - объем перевозимого груза от поставщика к ! потребителю. Система ограничений задачи не отличается от системы ограничений обычной транспортной задачи.

Математическая модель транспортной задачи по критерию времени имеет

Задача решается в следующем порядке. Находится начальное опорное решение #6. Определяется значение целевой функции "(#6). Все свободные клетки, которым соответствуют значения ,•• > "(#6), исключаются из рассмотрения. Занимать эти клетки нецелесообразно, так как увеличится значение целевой функции.

7.11. Пример краткого оформления решения

задачи методом потенциалов

Дано:

12,14,4 - предложение

9,10,11 - спрос

Решение.

1. Проверка плана на вырожденность:

12+14+4=9+10+11

30=30,

т.е. задача невырожденная, переходим к построению начального решения.

120