519_8_E92_2015_Efromeeva_E_V__Efromeev_N_M_Metody_issledovania_operatsiy_v_mashinostroenii_primery_zadachi_2-e_izdanie

1, … !); прибыль, получаемая предприятием при изготовлении и реализации единицы •-го вида продукта – !"; #" и $" – задаваемые нижняя и верхняя границы по объему выпуска •-го вида продукции.

Требуется составить такой план выпуска продукции, который был бы технологически осуществлен по имеющимся ресурсам всех видов, удовлетворял бы задаваемым ограничениям на выпуски каждого вида продукции и в то же время приносил бы наибольшую прибыль предприятию.

Таким образом, задача математически заключается в следующем:

найти такой план выпуска продукции % = (&' , … , &(), чтобы выполнялись

Несколько другая формулировка задачи.

Предприятие планирует организовать выпуск продукции n технологическими процессами. Производство единицы продукции j-м процессом требует затрат !*" единиц сырья i-го типа. Для закупки сырья предприятие имеет в своем распоряжении деньги в количестве B. Пусть 4" - рыночная стоимость единицы продукции, произведенной j-м процессом, а 5*- стоимость единицы сырья i-го типа. Цель предприятия – производство продукции наибольшей стоимости.

Задача оптимизации межотраслевых потоков

Каждая из n отраслей хозяйства производит только свой один специфический вид продукции, используемый в дальнейшем в производстве во всех n отраслях (в частности, в нулевом количестве). Если 6* – объем производства в i-й отрасли, &* – объем продукта i-го вида для внепроизводственного потребления, #*" – коэффициенты прямых затрат продукции j-го вида на производство в i-й отрасли единицы продукции i-го вида, 7* – максимально возможный объем производства в i-й отрасли, 4* – требуемое для внепроизведенного потребления количество продукции i-го вида, 8* – стоимость единицы продукции i-го вида, то задача ставится следующим образом.

Требуется найти такие объемы производства 6* и такой план выпуска конечной продукции &*, / = 1, … 2, при котором максимизируется общая стоимость произведенного конечного продукта – max∑(*-' 8*&* при выполнении ограничений:

на объем производства 0 ≤ 6* ≤ 7*, i=1,…n; на выпуск конечного продукта • ≥ " , i=1,…n; технологических ограничений на выпуск продукции $ ≥ ∑)'*, & '(' + • , . = 1, … /.

11

Транспортная задача

Подобная задача возникает в своем простейшем варианте, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителю. Поэтому здесь естественно возникает задача о наиболее рациональном прикреплении транспорта, правильном направлении перевозок груза, при котором полностью удовлетворяются потребности при минимальных затратах на транспортировку.

Итак, задача формулируется следующим образом.

Имеется m пунктов производства с объемами производства в единицу времени • , i=1,…m и n пунктов потребления !", j=1,… n.

Естественно, что потребление не должно превышать возможностей производства ∑$%& • ≥ ∑("%& !".

Затраты на перевозку единицы продукции из i-го пункта производства в j - й пункт потребления составляют ) ", а количество перевезенного продукта * ".

Требуется составить такой план перевозок, при котором суммарные затраты на них были бы минимальны min ∑$%& ∑("%& ) "* "

при условиях, что:

∙в каждый пункт потребления завозится требуемое количество продукта ∑$%& * " ≥ !", - = 1, … /;

∙из каждого пункта производства вывозится не более произведенного количества продукта ∑("%& * " ≤ • , 2 = 1, … 3;

∙и перевозимый объем продукта не может быть отрицательным

* " ≥ 0, 2 = 1, … 3, j = 1, … /.

Задача о выборе производственной программы

Эта задача была одной из первых практических задач линейного программирования, которая была решена в 1939 году известным русским математиком Л.В. Канторовичем.

На m предприятиях нужно произвести n продуктов в заданном ассортименте • , •!, ..., •". Если #$%, & = 1, … (, ) = 1, … *– рабочее время i-го предприятия, отводимое под j-й продукт, +$%– производительность i-го предприятия в единицу времени по выпуску j-го продукта, то задача о выборе производственной программы для случая, когда продукция дефицитна, производственные мощности ограничены и должны использоваться максимально полно, ставится следующим образом.

Требуется составить программу работы предприятий – указать время #$%, отведенное на производство каждого вида продукции на данном предприятии

12

таким образом, чтобы получить максимальный суммарный объем продукции в заданном ассортименте в единицу времени, т.е. необходимо найти ••• из условий, что:

произведенного на всех предприятиях.

Задача распределения ресурсов

Пусть имеется некоторое количество экономических ресурсов. Под термином ресурсы подразумеваются люди, деньги, машины, материалы для технологических процессов, вода для сельскохозяйственных и промышленных целей, топливо и т.д. Эти ресурсы потребляются различными способами, в результате чего получают некоторый доход, размер которого зависит от употребленного количества ресурсов и от выбранного процесса распределения.

Задача заключается в распределении ресурсов таким образом, чтобы максимизировать общий доход при следующих условиях:

Øдоходы, полученные от различных процессов, измеряются общей единицей;

Øдоход, полученный от рассматриваемого процесса, не зависит от количества ресурсов, выделенных для других процессов;

Øобщий доход получается как сумма доходов, полученных от отдельных процессов.

Замена оборудования

Одной из основных проблем промышленности является замена старого парка машин новым. Необходимо определить оптимальную политику модернизации и замены оборудования при различных предположениях относительно текущих издержек, производственных характеристик и будущего развития техники. Решения здесь принимаются почти ежегодно в зависимости от характерного для данного процесса периода времени, т.е. имеется многошаговый процесс решения.

Рассмотренные типы задач, решаемые методом линейного программирования, относятся к классу экономических задач. Этим методом решаются также задачи и других классов, например, о выборе диеты или

13

определении лучшего состава смеси, о рациональном использовании посевных площадей, о рациональном использовании трудовых ресурсов.

Линейное программирование используется также в различных расчетах химической технологии и т.д.

Несмотря на различное содержание задач, их физическую суть, математические постановки этих задач имеют много общего. В каждой из них требуется максимизировать или минимизировать некоторую линейную функцию нескольких переменных. Ограничения, положенные на совокупность этих переменных являются либо линейными уравнениями, либо линейными неравенствами. Поэтому далее в основном рассматривается только математическая постановка задачи линейного программирования и методы ее решения.

Нужно отметить, что в условиях руководства производством машинные методы оптимизации дают лишь количественную оценку ситуации.

Окончательное решение принимает человек.

14

2.Методы линейного программирования

2.1.Постановка задачи линейного программирования

Линейное программирование – область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума или минимума) линейной функции многих переменных при наличии линейных ограничений, т.е. равенств или неравенств, связывающих эти переменные.

Методы линейного программирования применяют к практическим задачам, в которых:

1)необходимо выбрать наилучшее решение (оптимальный план) из множества возможных;

2)решение можно выразить как набор значений некоторых переменных величин;

3)ограничения, накладываемые на допустимые решения специфическими условиями задачи, формулируются в виде линейных уравнений или неравенств;

4)цель выражается в форме линейной функции основных переменных. Значения целевой функции, позволяя сопоставлять различные решения, служат критерием качества решения.

Для практического решения экономической задачи математическими методами прежде всего ее следует записать с помощью математических выражений: уравнений, неравенств и т.п., т.е. составить экономико- математическую модель.

Исходя из отмеченных выше особенностей задач линейного программирования, можно наметить следующую общую схему формирования модели:

1)выбор некоторого числа переменных величин, заданием числовых значений которых однозначно определяется одно из возможных состояний исследуемого явления;

2)выражение взаимосвязей, присущих исследуемому явлению, в виде математических соотношений (уравнений, неравенств). Эти соотношения образуют систему ограничений задачи;

3)количественное выражение выбранного критерия оптимальности в форме целевой функции;

4)математическая формулировка задачи как задачи отыскания экстремума целевой функции при условии выполнения ограничений, накладываемых на переменные.

В свою очередь в линейном программировании существуют классы задач, структура которых позволяет создать специальные методы их решения, выгодно отличающиеся от методов решения задач общего характера. Так, в линейном программировании появился раздел транспортных задач, блочного программирования и др.

15

2.2. Основная задача линейного программирования. Построение математических моделей в виде задач линейного программирования

Задачей линейного программирования (ЗЛП) называется задача

отыскания экстремума (максимума или минимума) линейной функции от нескольких переменных при линейных ограничениях на эти переменные.

В общем виде задача линейного программирования состоит в максимизации (или минимизации) линейной функции

• = !"! + #"# + + %"%

при условии, что переменные xi имеют линейные ограничения вида

&!!"! + &!#"# + + &!%"% ≤ (=, ≥)-!, &#!"! + &##"# + + &#%"% ≤ (=, ≥)-#,

… … … … … … … … … … … … … … … …

&.!"! + &.#"# + + &.%"% ≤ (=, ≥)-., "/ ≥ 0, 1 = 1, … , 3.

Значения -/, 5, &/5 предполагаются известными.

Пример. Найти максимальное( ) значение функции

• !, " = 10 ! + 12 " → $%

при следующих ограничениях на переменные x1 и x2:

9! + 7 " ≤ 18,

&4 ! + 5 " ≤ 11,

!≥ 0, " ≥ 0.

Приведенная задача есть ЗЛП максимизации от двух переменных с ограничениями-неравенствами (могут быть и ограничения-равенства).

неотрицательности), а система линейных неравенств и (или) уравнений называется системой ограничений ЗЛП. Запись ЗЛП с ограничениями- неравенствами выглядит следующим образом:

Целевая функция

f (x1,x2 ) = 10x1 + 12x2 → max

ЗЛП является удобной математической моделью для большого числа экономических задач (планирование производства, расходование ресурсов, раскрой материалов, транспортные перевозки и т.д.). Рассмотрим на примерах процесс построения математической модели (в виде ЗЛП на максимум или минимум) для некоторых задач.

Основа построения математических моделей в виде ЗЛП - это, прежде всего, правильный выбор параметров экономической задачи (или некоторого процесса), через которые требуемая цель выражалась бы в виде линейной целевой функции, а ограничения на процесс записывались бы в виде системы линейных уравнений или неравенств.

2.2.1. Задача планирования производства продукции (задача линейного программирования на максимизацию)

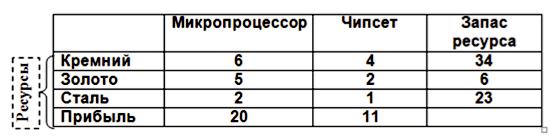
Некоторое предприятие в течение планового периода выпускает 2 вида продукции, например, микропроцессоры и чипсеты. При их производстве используются три вида ресурсов. Данные по их расходу на выпуск одного изделия, запасы ресурсов, а также прибыль от реализации единицы продукции приведены в табл.1.

Таблица 1

Требуется спланировать количество выпускаемых микропроцессоров и чипсетов таким образом, чтобы при данных условиях производства полученная прибыль была максимальна. Итак, цель задачи - получение максимальной прибыли. Выберем в качестве параметров, характеризующих процесс планирования производства продукции, число выпускаемых микропроцессоров (переменная x1) и выпускаемых чипсетов (переменная x2). Выразим через выбранные неизвестные суммарную прибыль от реализации всей продукции

•( !, ") = 20 ! + 11 ".

Она включает в себя прибыль от реализации всех микропроцессоров (20x1) и выпускаемых чипсетов (11x2). Цель задачи (максимизация прибыли) запишем в виде

#( !, ") = 20 ! + 11 " → %& .

Перейдем к формулировке ограничений. Структура всех трех

17

ограничений одинакова:

РАСХОД РЕСУРСА ≤ ЗАПАС РЕСУРСА

Теперь остается выразить полный расход ресурса через выбранные

Аналогично запишутся ограничения по второму и третьему видам

ресурсов

#5•• + 2•! ≤ 6, 2•• + •! ≤ 23.

Объединяя их в систему, получим

6•• + •! ≤ 34, $5•• + 2•! ≤ 6, 2•• + •! ≤ 23.

Далее, исходя из смысла введенных переменных, (число производимых

изделий не может быть отрицательным) на них необходимо наложить

ограничения неотрицательности:•• ≥ 0, •! ≥ 0.

Окончательно выпишем математическую модель задачи в форме ЗЛП.

&(••, •!) = 20•• + 11•! ≤ 34, 6•• + •! ≤ 34, $5•• + 2•! ≤ 6, 2•• + •! ≤ 23,

•• ≥ 0, •! ≥ 0.

Полученная модель может изменяться в зависимости от условий производства и реализации продукции. Например, при изменении условий реализации изменятся и коэффициенты в целевой функции. При изменении запасов ресурсов изменятся правые части в системе ограничений. При учете новых условий производства система ограничений дополнится новыми уравнениями или неравенствами.

После решения поставленной ЗЛП переменные x1 и х2 укажут плановое количество микропроцессоров и чипсетов для получения максимальной прибыли, а разность между правой и левой частями каждого неравенства даст остаток ресурса каждого вида.

18

2.2.2. Задача о составлении оптимального производственного процесса

(задача линейного программирования на минимизацию)

На заводе предстоит решить, какое количество чистой стали и какое количество металлолома следует использовать для приготовления (из соответствующего сплава) литья для одного из своих заказчиков. Пусть производственные затраты на 1 т стали составляют 3 усл. ед., а затраты на 1 т металлолома – 5 усл. ед. (последняя цифра больше предыдущей, так как использование металлолома связано с его предварительной очисткой). Заказ предусматривает поставку не менее 5 т литья. Предположим, что предназначенные для литья запасы чистой стали составляют 4 т, а металлолома - 6 т. Отношение веса металлолома к весу чистой стали в сплаве не должно превышать 7/8. Производственно-технологические условия таковы, что на процессы плавки и литья не может быть отведено более18 ч, при этом на 1 т стали затрачивается от 2,5 до 3 ч, а на 1 т металлолома – от 1,5 до 2 ч. Цель

завода – выполнить заказ с минимальными производственными затратами, выраженными• ив•условных единицах.

Пусть # – количество чистой стали и металлолома соответственно.

Добавив к полученным ограничениям условия неотрицательности (xi равно нулю, если i-я составляющая не используется в сплаве), окончательно запишем ЗЛП.

В приведенных примерах все ограничения имеют вид линейных неравенств. Это так называемые нежесткие ограничения (ресурс может быть

израсходован полностью, а может и частично). Однако можно ставить и жесткие ограничения в виде линейных уравнений. Так, в первом примере требование полного использования кремния приводит к ограничению

6! + 4 " = 34.

2.3.Примеры решения задач

Задача №1.

Выполнить заказ по производству 32 изделий И1 и 4 изделий И2 взялись бригады Б1 и Б2. Производительность бригады Б1 по производству изделий И1 и И2 составляет соответственно 4 и 2 изделия в час, фонд рабочего времени этой бригады 9,5 ч. Производительность бригады Б2 – соответственно 1 и 3 изделия в час, а ее фонд рабочего времени – 4 ч. Затраты, связанные с производством единицы изделия, для бригады Б1 равны соответственно 9 и 20 руб., для бригады Б2 – 15 и 30 руб.

Составьте математическую модель задачи, позволяющую найти оптимальный объем выпуска изделий, обеспечивающий минимальные затраты на выполнение заказа.

Решение.

Переменные задачи

Искомыми величинами в задаче являются объемы выпуска изделий. Изделия И1 будут выпускаться двумя бригадами Б1 и Б2. Поэтому необходимо различать количество изделий И1, произведенных бригадой Б1, и количество изделий И1, произведенных бригадой Б2. Аналогично, объемы выпуска изделий И2 бригадой Б1 и бригадой Б2 также являются различными величинами. Вследствие этого в данной задаче 4 переменные. Для удобства восприятия будем использовать двухиндексную форму записи XIJ – количество

изделий ИJ (j=1,2), изготавливаемых бригадой БI (i=1,2), а именно,

X11 – количество изделий И1, изготавливаемых бригадой Б1, [шт.]; X12 – количество изделий И2, изготавливаемых бригадой Б1, [шт.];

X21 – количество изделий И1, изготавливаемых бригадой Б2, [шт.];

X22 – количество изделий И2, изготавливаемых бригадой Б2, [шт.].

20