
519_8_E92_2015_Efromeeva_E_V__Efromeev_N_M_Metody_issledovania_operatsiy_v_mashinostroenii_primery_zadachi_2-e_izdanie
.pdf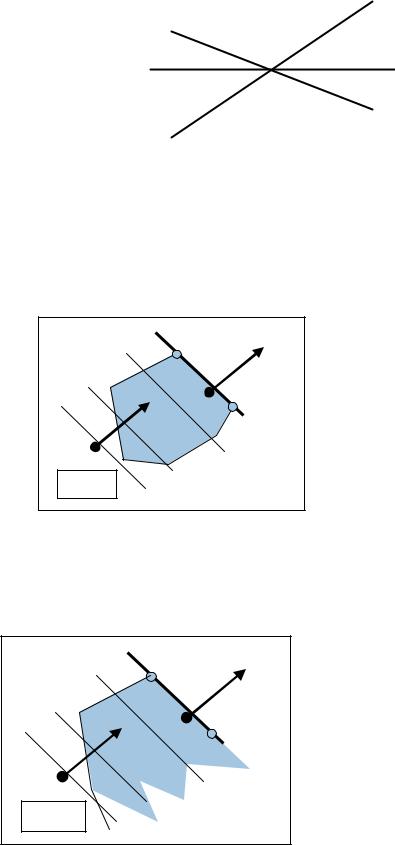
ЗЛП разрешима:
ü множество решений состоит из одной точки. Она же и является оптимальной (рис. 21);
Рис. 21
üединственное оптимальное значение ЗЛП;
üоптимальное решение ЗЛП не единственно:
Вектор N перпендикулярен одной из сторон множества решений. В этом случае оптимальной является любая точка отрезка AB (рис 22).
A |
N |
|
|
MAX |
|
Рис. 22 |
|
В следующем примере (рис. 23) оптимальными решениями являются все точки луча AB:
A |
N |
|
|
MAX |
|
Рис. 23 |
|
41
Графически также могут быть решены ЗЛП и с большим числом их
переменных, если их удастся свести к ЗЛП с двумя переменными, например, рассмотрим ЗЛП:
• = ! |
+ |
|
" + |
# + |
|
$ + % → '( , |
||||
(1) |
- |
2 |
|
! + 4 |
" |
+ 5 |
# |
= 12, |
||
7 |
5 ! |
− |
" |
− 2 |
$ |
= 8, |
||||
|
|
, |
! + 10 |
" |
+ 7 % = 70, |
|||||
|
|
! |
", |
#, |
$ |
, % |
≥ 0. |
|||
Отбрасываем переменные x3, x4, x5 из системы уравнений. Для этого в системе ограничений заменяем их неравенствами. А в целевой функции их
заменяем через x и x2 |
. Тогда задача может быть приведена к виду |
|||||||
6 = |
! + |
1 |
− 2 ! − 4 |
") |
1 |
− 5 ! + |
1 |
(70 − 7 ! − 10 ") |
" + 5 (12 |
− 2 (8 |
") + 7 |
||||||
|
|
→ '( ; |
|
2 ! + 4 |
" ≤ 12, |
|
|
|
|
|
|
(2) |
97 |
5 ! − |
" ≥ 8, |
|
|
|
|
|
! + 10 |
" ≤ 70, |
|
|
||
|
|
|
|
|
!, " |
≥ 0. |
|
|
После графического решения системы (2) x3, x4,x5 определяют из (1).
3.4. Пример краткого оформления решения задач линейного программирования графическим методом
Дано: |
• = 4•• + 2•• → • •, |
|
|
|
• + 2•• ≤ 10, |
|
2•• − •• ≥ 1, |
|
! •• − 3•• ≤ 2, |
|
•• ≥ 0, •• ≥ 0. |
42
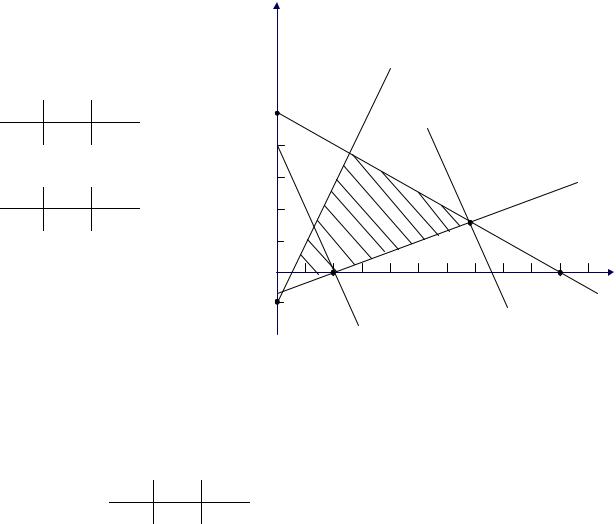
Решение.
1. Строим наши прямые на плоскости x10x2 и определяем ограничения (рис. 24);
|
x1 + 2x2 = 10 |
X2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
X1 |
0 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
X2 |
5 |
|
0 |
|
|
|
|
|
|
= |
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2x1 |
– x2 = 1 |
|
|
|
|
-X |
2 |
|
||
|
|
|
|
|
|
|
|||||
|
|
|
2 |
X |
1 |
|
|
||||
X1 |
0 |
|
0.5 |
|
|
|
|
|
|
||
|
|
5 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
X2 -1 0
4
x1 - 3x2 = 2 X1 0 2
X2 -0.6 0
2 |
7 |
-1 |
|
|
P |
|
|
2 |
|
= |
|
X2 |
|
|
-3 |
|
|
X1 |
|
|
10 |
X |
|
|
|
X1 |
|
+ |
|
|
||
|
|
|
|
||
|
1 |
2X |
|
|
|
|
|
|
= |
||
|
|
|
2 |
10 |
|
|
|
|
|
|
|
Рис. 24
2.Строим любую прямую, соответствующую целевой функции, и определяем направление возрастания (убывания);
P = 4x1 + 2x2
X1 0 2
X2 4 0
3.Определяем граничную точку (отрезок), в которой целевая функция принимает max;
4.Вычисляем эти точки (точку), т.е. решаем совместно уравнения, на
пересечении тех прямых, где находится точка (отрезок или прямая):
----------------- |
|
|
|
X1 – 3X2 = 2 |
|
|
|
X1 + 2X2 = 10 |
|
|
|
---------------- |
|
|
|
5 |
• = 8; |
|
|
Х |
= 8/5; |
|
|
• |
|
|
|
ХХ = 2 + 3*8/5 = 2 + 24/5 = (10+24)/5 = 34/5; |
|||
P = 4*34/5 + 2*8/5 = 136/5 + 16/5 = 152/5. |
|||
Ответ: P=152/5 при |
Х |
= 8/5. |
|
|
|
= 34/5, Х• 43 |
|
3.5. Задачи для самостоятельного решения
Решить графически задачи линейного программирования(1-9):
! |
! + |
" |
≤ 6, |
|
|
$ |
2 |
! |
|
||||
1. |
" |
|
2. |
|
$ + 4 ! ≤ 11, |
||||||||
2 |
! |
|
! |
" |
≤ 1, |
|
|
& |
2 |
$ + 3 |
! ≤ 7, |
||
|
|
|
≥ 6, |
|
|
$ + |
! ≤ 10, |
||||||
|
|
− |
≥ 1, |
|
|
|
|
|
|
|
|||
0,5 |
!! |
+ |
"" |
≥ |
. |
|
, |
|
|
( ≥ 0, ) = 1,2 . |
|||
|
|
! ≥ 1 |
−4 |
|
|
|
|
|
|
||||
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
3. |
|
$ |
2 |
|
! |
! ≥ 0, |
|
|
|
|
|
|
$ − |
||
|
|
& |
0,5 |
$ − |
! ≤ 0, |
||
|
|
|
( |
$ + |
! ≤ 5, |
||
|
|
|
|
≥ 0, ) = 1,2 . |
|||
5. |
|
$ −4 !$ + |
! ≥ 4, |
||||
|
|
& |
2 |
$ |
+ 3 |
! ≤ 10, |
|
|
|
|
( |
$ |
− 2 |
! ≤ 4, |
|
|
|
|
|
≥ 0, ) = 1,2 . |
|||
7. |
3 |
|
+ 5 |
|
min |
||
|
|
"3!" |
+#2!# ≥ 36, |
||||
|
|
*3!" |
+ 5!# ≥ 45 |
||||
|
|
|
|
!", !# ≥ 0 . |
|||
9. 2!" + !# → 9':,!" + !# ≤ 12, 2!" − !# ≤ 12,2!" − !# ≥ 0,2!"!+# ≥!#0≥. 4,
4.4 $$ + 3 !! ≥ 8,
−$ + 4 ! ≤ 12,
2 $ −$ ≤3!4,≤ 5,( ≥ 0, ) = 1,2 .
6. |
$ |
|
! |
|
|
−4!" − !# ≥ −3, |
|||
|
• |
!" − !# ≤ 2, |
||
|
!" |
+ 2!# ≥ 3, |
||
|
|
!& ≥ 0, ' = 1,2 . |
||
8. |
-3 " - 2 |
# |
min |
|
|
|
5!" + !# ≥ 6, |
||
|
−!" |
+ 3!# ≥ 4, |
||
|
|
2!" − !# ≤ 6, |
||
|
3!" |
− 4!# ≤ 0, |
||
|
|
!" |
, !# |
≥ 0 . |
44
10.Предприятие электронной промышленности выпускает две модели
радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем первой линии − 60 изделий, второй линии − 80 изделий. На радиоприемник первой модели расходуется
15 однотипных элементов электронных схем, на радиоприемник второй модели − 10 таких же элементов. Максимальный суточный запас используемых элементов равен 950 единиц. Прибыли от реализации одного радиоприемника первой и второй моделей равны 400 рублей и 200 рублей соответственно. Определите оптимальные суточные объемы производства первой и второй моделей на основе графического решения задачи.
Графически решить задачи линейного программирования(11-17):
11. |
|
|
! |
" |
|
≤ 16, |
||
|
|
2 |
+ 4 " |
|||||
|
|
|
−4! |
! |
+ 2 " |
≤ 8, |
||
|
|
|
6 ! |
|
" |
≥ 9, |
||
|
|
|
+ 3 |
|
||||
|
|
|
|
|
|
. |
||
|
|
|
+ 5 " = 30, |
|||||
|
|
! |
!," ≥ 0 |
|
||||
13. |
$ |
|
−#$%+ 3#% ≥ 10, |
|||||
|
|
#$ + #% |
≤ 6, |
|||||
|
|
|
#$$+ 4#%%≥ 3, |
|||||
|
|
|
−# |
+ 4# |
≥ 2, |
|||
|
|
|
#$,% |
≥ 0. |
||||
15. |
|
$2#$ +%3#% ≤ 24, |
||||||
|
|
−8#$ |
+ 3#% |
≤ 24, |
||||
|
|
8 |
2#$ − 3#% ≤ 12, |
|||||
|
|
4#$ |
+ 3#% |
≥ −12. |
||||
17. |
#$ + 4#% |
→ -/#, |
||||||
|
|
|
−4#$ |
+ #% ≤ 4, |
||||
|
|
−#$ + #% |
≤ 5, |
|||||
|
|
|
−#$$ + 2#%% ≤ 2, |
|||||
|
|
|
3# |
+ 4# |
≥ 12, |
|||
|
|
|
#$,% |
≥ 0. |
||||
12. ! #$ +" 3#% ≥ 3,
#$ + #% ≥ 5,−2##$+≤#4,≥ 2,
#$ ≥%0.
$,%
14. $ −#$%+ #% ≤ 5, 85#$ − 2#% ≤ 20, 8#$ − 3#% ≥ 0, 5#$ − 6#% ≤ 0.
16. $2#$ %+ #% ≥ −4, 8 #$ + #% ≥ 0,
#$ + 2#% ≥ 2,
#$ − #% ≤ 2.
45
18.Механический цех может изготовить за смену 600 деталей №1 или 1200 деталей №2. Производственная мощность термического цеха, куда эти детали поступают на термообработку в тот же день, позволяет обрабатывать за смену 1200 деталей № 1 или 800 деталей № 2. Цены на детали одинаковые.
Определить ежедневный производственный план выпуска деталей, максимизирующий товарную продукцию предприятия, при следующих дополнительных условиях:
а) оба цеха работают в одну смену; б) механический цех работает в три смены, а термический — в две смены;
в) предприятие работает в две смены, при этом деталей № 1 должно быть изготовлено не более 800 шт., а деталей № 2 — не более 1000 шт.
19.Для изготовления изделий А и В фабрика расходует в качестве сырья сталь и цветные металлы, имеющиеся в ограниченном количестве. Указанные изделия производят с помощью токарных и фрезерных станков. Определить план выпуска продукции, при котором будет достигнута максимальная прибыль. Исходные данные приведены ниже:
Вид ресурса |
Объем |
Нормы расхода на одно изделие |
||
ресурса |
А |
В |
||
|
||||
|
|
|
|
|
Сталь, кг |
570 |
10 |
70 |
|
|
|
|
|
|
Цветные металлы, кг |
420 |
20 |
50 |
|
|
|
|
|
|
Токарные станки, |
5600 |
300 |
400 |
|
станко-час |
||||
|
|
|
||
Фрезерные станки, |
3400 |
200 |
100 |
|
станко-час |
||||
|
|
|
||
Прибыль, ден. ед. |
3 |
8 |
||
|
|
|
|
|
20.Сформулировать математически и решить графически следующую задачу: имеются три технологических процесса для выделения из руды двух нужных веществ А и В. Из каждой тонны руды при применении процессов I, II, III получается соответственно, 0,4 и 0,6; 0,6 и 0,4; 0,2 и 0,2 кг вещества
Аи В. При этом затраты составляют 5 тыс. руб. для процесса I, 6 тыс. руб. для процесса II и 1 тыс. руб. для процесса III. Определить оптимальное распределение 10 т руды по процессам I, II, III, минимизирующее затраты, если необходимо получить не менее 3 кг каждого вещества.
21.Предприятие для выпуска некоторой продукции использует две технологии (два способа). При этом необходимы три вида ресурсов. Известно: •• ед.
=1, 2, 3) — запасы ресурсов;!•", ед./ч ( = 1, 2, 3; # = 1, 2) — затраты -го
вида ресурса за 1 час работы с использованием #-й технологии; %", руб./ч (# = 1, 2) — прибыль предприятия от реализации продукции, выпускаемой
46
за 1 час работы с использованием •-й технологии; , ч — общее время работы предприятия по обеим технологиям.
Найти, сколько времени по каждой технологии должно работать предприятие, чтобы обеспечить максимум прибыли от реализации выпускаемой продукции:
а) при = 500 ч; |
б) при |
• |
= 300 ч. |
|
|||
Исходные данные приведены ниже: |
|
|
|
|
|||
|
Вид ресурса |
Запасы |
Затраты ресурсов "!# за 1 |
||||
|
ресурса, |
час работы по технологии |
|||||
|
|
||||||
|
|
ед. ! |
|
|
№ 1 |
|
№2 |
|
1 |
400 |
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
2 |
1500 |
|
|
3 |
|
5 |
|
|
|
|
|
|
|
|
|
3 |
900 |
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
Прибыль $#, руб./ч |
|
|
300 |
|
400 |
|
|
|
|
|
|
|
|
|
22.Из пункта А в пункт В ежедневно отправляются скорые и пассажирские поезда. Наличный парк вагонов разных типов, из которых ежедневно можно комплектовать данные поезда, и число пассажиров, вмещающихся в каждом из вагонов, приведены ниже:
Вагон |
Число вагонов в поезде |
Число |
Парк |
||
скором |
пассажирском |
пассажиров |
вагонов |
||
|
|||||
Багажный |
1 |
1 |
— |
12 |
|
|
|
|
|
|
|
Почтовый |
1 |
— |
— |
8 |
|
|
|
|
|
|
|
Плацкартный |
5 |
8 |
58 |
81 |
|
|
|
|
|
|
|
Купейный |
6 |
4 |
40 |
70 |
|
|
|
|
|
|
|
Мягкий |
3 |
1 |
32 |
26 |
|
|
|
|
|
|
|
Определить:
а) количество скорых и пассажирских поездов, при которых число перевозимых пассажиров достигает максимума; б) оптимальное количество поездов для случая, когда железная дорога не
может пропустить более шести пассажирских поездов.
47

4. Графический способ решения ЗЛП с n переменными
Графическим методом решаются задачи линейного программирования,− ≤ 2 записанные в каноническом виде и удовлетворяющие условию • ! , где
• – число неизвестных системы ограничений; ! – ранг системы векторов условий. Если уравнения системы ограничений линейно независимы, то ранг ! равен числу уравнений системы #.
4.1. Пример графического решения задачи линейного программирования с $ переменными
−%& − %' + %( + 3%) + 7%* → #-•, |
|||
Решить задачу линейного программирования: |
|
||
|
−%& + %' + %( + 2%) − 3%* = 4, |
||
/ |
%& + %' + 4%( + %) |
− 8%* |
= 3, |
%' + %( − 4%* |
= −4, |
|
|
|
%0 ≥ 0, 6 = 1, 2,3, 4, 5. |
|
|
Метод применим, так как • − ! = 5 − 3 = 2. |
|
|
|
Методом Жордана – Гаусса приведем систему уравнений-ограничений задачи к равносильной системе уравнений. Одновременно исключим разрешенные неизвестные из целевой функции.
%& |
|
%' |
%( %) %* |
< |
|
|||||
-1 |
|
|
1 |
|
4 |
система |
||||
1 |
||||||||||
|
|
2 |
-3 |
|
||||||
1 |
|
1 |
4 |
1 |
-8 |
|
3 |
уравнений- |
||
0 |
|
1 |
1 |
0 |
-4 |
|
-4 |
ограничений |
||
-1 |
|
-1 |
1 |
3 |
7 |
|
0 |
целевая функция |
||
-1 |
|
1 |
1 |
2 |
-3 |
|
4 |
|
||
2 |
|
0 |
3 |
-1 |
-5 |
|
-1 |
|
||
|
1 |
|
0 |
0 |
-2 |
-1 |
|
-8 |
|
|
-2 |
|
0 |
2 |
5 |
4 |
|
4 |
|
||
0 |
|
1 |
1 |
0 |
-4 |
|
-4 |
|
||
0 |
|
0 |
|
3 |
3 |
-3 |
|
15 |
|
|
1 |
|
0 |
0 |
-2 |
-1 |
|
-8 |
|
||
0 |
|
0 |
2 |
1 |
2 |
|
-12 |
|
||
0 |
|
1 |
0 |
-1 |
-3 |
|
-9 |
|
||
0 |
|
0 |
1 |
1 |
-1 |
|
5 |
|
||
1 |
|
0 |
0 |
-2 |
-1 |
|
-8 |
|
||
0 |
|
0 |
0 |
-1 |
4 |
|
-22 |
|
||
|
|
|
|
|
|
|
|
48 |
|
|
Использую последнюю часть таблицы, запишем ЗЛП в преобразованном виде |
|||||
− |
! + 4 |
" + 22 → $%&, |
|||
|
) − |
! − 3 |
" |
= |
−9, |
' |
* + |
! − |
" |
= |
5, |
.-≥ 0, 1!= 1 |
" = 8, |
||||
− 2 |
− |
|
|
− |
|
|
|
|
, 2, 3, 4, 5. |
||
Отбросим в уравнениях-ограничениях неотрицательные разрешенные |
|||||||||||||||||
неизвестные |
|
), |
* и заменим знак равенства знаками неравенства |
" ≤ ", |
|||||||||||||
получим |
вспомогательную задачу ЛП с двумя переменными: |
|
|||||||||||||||
|
-, |
|
− |
|
! |
+ 4 |
|
" + 22 → $%&, |
|
||||||||
|
|
|
|
− |
|
|
|
− 3 |
|
≤ |
−9, |
|
(1) |
|
|||
|
|
|
|
|
|
|
− |
|
|
" |
|
−8, |
5. |
|
|
||
|
|
|
|
−2 |
|
! − |
|
|
(2) |
|
|||||||
|
|
|
|
|
! |
! |
|
" |
≤"5, |
, |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
≤ |
|
(3) |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
. ≥ 0, 1 = 4
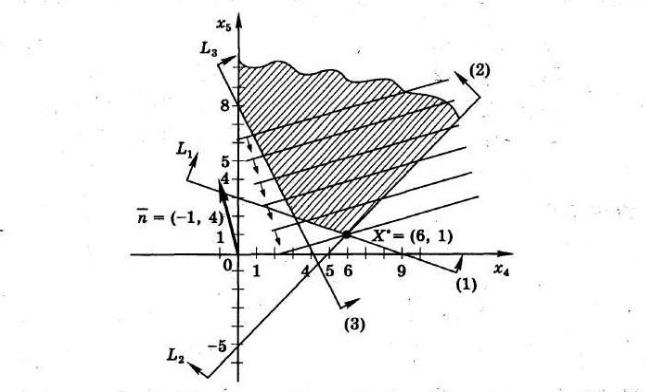
Решаем задачу22 графическим методом (рис. 25). Свободный член в целевой функции на отыскание оптимального решения не влияет и учитывается только при вычислении значения целевой функции.
Рис. 25
49
Находим оптимальное решение вспомогательной задачи • = |
! ∩ #: |
|||||
+ $ |
−&' − 3&( = −9, |
( !) |
|
|||
&' − &( |
= 5 |
( #) |
|
|
||
|
|
−4&( |
= −4; |
|
|
|
|
|
&( = 1, &' = 6; |
|
|
|
|
|
|
& = (6;1) |
|
|
|
|
Вычисляем минимальное значение целевой функции −1 ∙ 6 + 4 ∙ 1 + 22 = 20.
Находим оптимальное решение исходной задачи. Для этого используем |
|||
систему ограничений в разрешенном виде |
|||
|
7 |
&# |
− &' − 3&( = −9, |
|
&8 + &' − &( = 5, |
||
Вычисляем &#, &8 и &!: |
&! |
− 2&' − &( = −8, |
|
|
+ 3&( = −9 + 6 + 3 ∙ 1 = 0, |
||
&# |
= −9 + &' |
||
&! |
&8 = 5 − &' + &( = 5 − 6 + 1 = 0, |
||
= −8 + 2&' + &( = −8 + 2 ∙ 6 + 1 = 5. |
|||
Получаем & = (5;0; 0; 6; 1. ) |
|
|
|
Ответ: ?@AB = 20 при & = (5;0; 0;6; 1).
50
