
361
.pdf
1
МИНИСТЕРСТВО ВНУТРЕННИХ ДЕЛ РОССИЙСКОЙ ФЕДЕРАЦИИ
МОСКОВСКИЙ УНИВЕРСИТЕТ
Ю. Н. Александров, В. М. Смирнов
СБОРНИК ЗАДАЧ ПО ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
Учебное пособие
Москва МосУ МВД России
2013
2
ББК 2
А-46
Александров, Ю. Н.
Сборник задач по дифференциальным уравнениям : учебное пособие / Ю. Н. Александров ; В. М. Смирнов. – М. : Московский университет МВД России, 2013. – 67 с.
В пособии представлены задания по обыкновенным дифференциальным уравнениям, а также краткие теоретические сведения и примеры решения типовых задач. В сборник включены задания по следующим типам дифференциальных уравнений: дифференциальные уравнения 1-го порядка (с разделяющимися переменными, однородные, линейные, Бернулли, в полных дифференциалах), дифференциальные уравнения высших порядков, а также линейные дифференциальные уравнения с постоянными коэффициентами.
Предназначено для обучающихся по специальностям «Экономическая безопасность» и «Безопасность информационных технологий в правоохранительной сфере», а также может быть полезно студентам, курсантам и слушателям, изучающим обыкновенные дифференциальные уравнения по другим специальностям.
ББК 2
Рецензенты: начальник кафедры информационной безопасности Московского университета МВД России, кандидат технических наук К. К. Борзунов; старший преподаватель кафедры информационных технологий управления органами внутренних дел Академии управления МВД России, кандидат технических наук В. И. Кононенко.
©Московский университет МВД России, 2013
©Александров Ю. Н., 2013
©Смирнов В. М., 2013
3
Оглавление |
|
Введение ...................................................................................... |
4 |
Глава 1. Дифференциальные уравнения первого по- |
|
рядка .................................................................................................. |
6 |
§ 1. Основные понятия и определения...................................... |
6 |
§ 2. Простейшие дифференциальные уравнения..................... |
13 |
§ 3. Уравнения с разделяющимися переменными................... |
16 |
§ 4. Однородные дифференциальные уравнения первого по- |
|
рядка ................................................................................................... |
20 |
§ 5. Линейные дифференциальные уравнения первого по- |
|
рядка...................................................................................................... |
22 |
Метод Бернулли........................................................................... |
22 |
Метод вариации произвольного постоянного.......................... |
24 |
§ 6. Уравнение Бернулли............................................................ |
26 |
§ 7. Дифференциальные уравнения в полных дифферен- |
|
циалах................................................................................................. |
29 |
Глава 2. Дифференциальные уравнения высших по- |
|
рядков................................................................................................ |
33 |
§ 1. Основные понятия и определения...................................... |
33 |
§ 2. Дифференциальные уравнения высших порядков, до- |
|
пускающие понижение порядка...................................................... |
34 |
Уравнения вида ...................................................... |
34 |
Уравнения, не содержащие искомой функции в явной |
|
форме.................................................................................................. |
35 |
Уравнения, не содержащие переменной в явной форме ..... |
37 |
Глава 3. Линейные дифференциальные уравнения с |
|
постоянными коэффициентами................................................... |
41 |
§ 1. Введение в комплексные числа .......................................... |
41 |
§ 2. Однородные линейные дифференциальные уравнения с |
|
постоянными коэффициентами....................................................... |
45 |
§ 3. Неоднородные линейные дифференциальные уравне- |
|
ния с постоянными коэффициентами............................................. |
50 |
Ответы и указания к заданиям для самостоятельного |
|
решения............................................................................................. |
61 |
Библиографический список.................................................... |
66 |
4
ВВЕДЕНИЕ
Дифференциальные уравнения – раздел математики, неизменно присутствующий в программе подготовки как будущих инженеров, так и будущих экономистов. Этот раздел обычно изучается в конце курса математики, поскольку и понятие дифференциального уравнения, и методы их решения основываются на знаниях других разделов математики, таких, как дифференциальное и интегральное исчисления, алгебра, аналитическая геометрия и др. Это вызывает определенные трудности, поскольку при решении дифференциального уравнения может потребоваться найти несколько интегралов, решить систему линейных уравнений, вычислить определитель и т.п.
Зачем изучать столь сложный раздел математики? Зачем нужны дифференциальные уравнения?
Практически в любой предметной области, будь то техника, экономика или психология, объектом изучения становятся некоторые числовые величины, например, положение объекта (его координаты), сила тока, прибыль, объем производства, наблюдаемые в течение времени, а также скорости их изменения. В каждой предметной области выводятся свои законы, связывающие эти величины, их скорости изменения, а иногда и ускорения. Вспомнив, что скорость изменения величины – фактически первая производная этой величины по времени, а ускорение – вторая, получаем, что практически любой закон – некоторое дифференциальное уравнение, а решение данного дифференциального уравнения – зависимость этой изучаемой величины от времени.
Существует множество типов дифференциальных уравнений, а также методов их решения. Большинство из них по силам только ма- тематикам-профессионалам. Доказано, что часть дифференциальных уравнений невозможно решить аналитически.
Данное учебное пособие предназначено не для математиковпрофессионалов, поэтому здесь представлены краткие необходимые теоретические основы дифференциальных уравнений, а также методы решения простейших дифференциальных уравнений. При необходимости изучения дифференциальных уравнений в более полном объеме рекомендуется изучить учебники и учебные пособия, приведенные в списке литературы.
5
Цель данного пособия – дать представление о дифференциальных уравнениях и отработать навыки решения типовых наиболее часто встречающихся дифференциальных уравнений.
Учебное пособие разбито на три главы: «Дифференциальные уравнения первого порядка», «Дифференциальные уравнения высших порядков», «Линейные дифференциальные уравнения с постоянными коэффициентами». Каждая глава, в свою очередь, разбита на параграфы.
Каждый параграф начинается с краткого изложения теории, основных формул и с образцов решения типовых задач. Далее в каждом параграфе представлены задания для самостоятельного решения обучаемыми (ответы и указания к этим задачам расположены в конце учебного пособия). Завершается параграф заданиями для контроля знаний (по 20 заданий каждого типа) для выдачи индивидуального домашнего задания и/или проведения самостоятельных и контрольных работ.

6
Глава 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
§ 1. Основные понятия и определения
Обыкновенным дифференциальным уравнением1 называется
уравнение, связывающее независимую переменную , искомую функцию и ее производные ′, ′′, … , , т.е. уравнение вида:
, , , , … , 0.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
′′ ′ sin 2 – дифференциальное уравнение 2-го порядка.
2 – дифференциальное уравнение 1-го порядка, так
как ′ . 2 0 – дифференциальное уравнение 1-го
порядка. Для приведения данного уравнения к виду, указанному в определении, достаточно разделить обе части уравнения на и за-
менить на ′.
′′′ – дифференциальное уравнение 9-го порядка.
Решением дифференциального уравнения n-го порядка на ин- |
|
тервале , |
называется функция , определенная на ин- |
тервале !, " |
вместе со своими производными до n-го порядка |
включительно, |
и такая, что подстановка функции в диф- |
ференциальное уравнение превращает последнее в тождество по
на !, ".
1 В математике также рассматриваются дифференциальные уравнения, где искомая неизвестная функция зависит от двух или более независимых переменных. Такие дифференциальные уравнения называются дифференциальными уравнениями в частных производных. В данном пособии рассматриваются только обыкновенные дифференциальные уравнения, поэтому далее везде под дифференциальными уравнениями будут подразумеваться обыкновенные дифференциальные уравнения.

|
7 |
Пример 1. Доказать, |
что функция sin cos является ре- |
шением уравнения ′′ 0 на интервале ∞, ∞ . |
|
Решение. Найдем первую и вторую производные данной функции: |
|
′ cos sin , |
′′ sin cos . |
Подставляя выражения ′ и ′′ в данное дифференциальное урав-
нение ′′ 0, получим тождество:
sin cos sin cos & 0 .
График решения дифференциального уравнения называется ин-
тегральной кривой.
Общий вид дифференциального уравнения первого порядка:
, , ′ 0.
Если из этого уравнения удается выразить ′:
′ , ,
то получится уравнение первого порядка, разрешенное относительно производной.
Задачей Коши называют задачу нахождения решения |
||
уравнения |
′ , , удовлетворяющего начальному условию |
|
( ( |
| + , ( |
). |
|
(другая запись ) |
|
Геометрически это означает, что ищется интегральная кривая, которая проходит через указанную точку - (, ( .
y
- (, (
(
x
O |
( |
Теорема существования и единственности решения задачи Коши. Пусть дано дифференциальное уравнение ′ , , где функция , определена в некоторой области . плоскости /, содержащей точку (, ( . Если функция , удовлетворяет условиям:
8
а) , есть непрерывная функция двух переменных x и y в области .;
б) , имеет частную производную 001 , ограниченную в об-
ласти ., то найдется интервал ( 2, ( 2 , на котором существует
единственное решение данного уравнения, удовлетворяющее условию ( (.
Общим решением дифференциального уравнения 3′ 4 5, 3 |
||
называется функция |
, 6 , зависящая от одной произвольной |
|
постоянной 6, и такая, что: |
|
|
а) она удовлетворяет уравнению ′ , при любых допус- |
||
тимых значениях постоянной 6; |
|
|
б) каково бы ни было начальное условие ( ( , можно по- |
||
добрать такое значение 6( постоянной 6, что решение |
, 6( |
|
будет удовлетворять этому начальному условию. |
|
|
При этом предполагается, что точка (, ( принадлежит области, |
||
где выполняются условия существования и единственности решения |
|
соответствующей задачи Коши. |
3 4 5, 3 |
Частным решением дифференциального уравнения |
|
называется решение, получаемое из общего решения |
, 6 при |
каком-либо определенном значении произвольной постоянной 6. |
|
Пример 2. Проверить, что функция 2 6 является общим |
|
решением дифференциального уравнения ′ 2, и найти частное ре- |
|
шение, удовлетворяющее начальному условию 1 2. Дать гео- |
|
метрическую интерпретацию результата. |
|
Решение. Проверим условия а) и б) из определения общего реше-
ния дифференциального уравнения: |
|
|
||
а) функция |
2 6 действительно удовлетворяет уравнению |
|||
′ 2 при любых значениях произвольной постоянной 6, так как |
||||
′ 2 6 ′ 2; |
|
условие ( (. |
|
|
б) зададим |
произвольное |
начальное |
Под- |
|
ставляя ( |
и ( в |
равенство |
2 6, найдем, |
что |
6 ( 2(. Подставив это значение в данную функцию, получаем |
||||
решение 2 ( 2(, |
удовлетворяющее произвольным |
на- |
||
чальным условиям ( (. Действительно, при ( получаем
2( ( 2( (.
9
Таким образом, функция 2 6 является общим решением
дифференциального уравнения ′ 2.
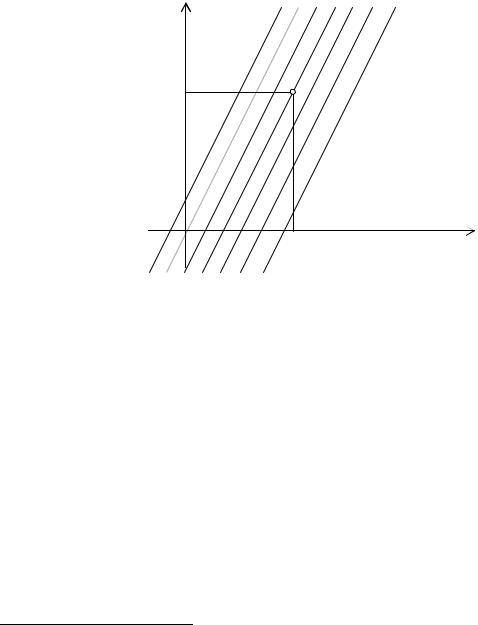
Полагая ( 1 и ( 2, получим частное решение 2. Общее решение дифференциального уравнения 2 6 опре-
деляет на плоскости / множество параллельных прямых с угловым коэффициентом 8 2. Через каждую точку на плоскости - (, ( можно провести ровно одну прямую с указанным наклоном, т.е. проходит единственная интегральная кривая2 2 ( 2(. Частное решение 2 определяет одну из этих интегральных кривых, а именно: прямую, проходящую через начало координат.
2
y
( - (, (
x
O |
( |
Соотношение вида 9 , , 6 0, неявно определяющее общее решение дифференциального уравнения, называется общим инте-
гралом дифференциального уравнения первого порядка, или общим
решением дифференциального уравнения первого порядка, заданным неявно.
Соотношение, получаемое из общего интеграла дифференциального уравнения первого порядка при конкретном значении постоян-
ной 6, называется частным интегралом дифференциального урав-
нения первого порядка.
По виду решаемого дифференциального уравнения трудно, а иногда и невозможно, определить, можно ли из общего интеграла дифференциального уравнения выразить общее решение этого диффе-
2 В данном случае интегральная кривая оказалась прямой.

10
ренциального уравнения. Поэтому в задачах на нахождение общего решения дифференциального уравнения в качестве ответа часто подразумевают возможность указания общего интеграла дифференциального уравнения, т.е. общее решение дифференциального уравнения находится в явном или в неявном виде.
Задания для самостоятельного решения
№1. Проверить, что заданная функция 3 6 является общим решением дифференциального уравнения ′ 3, и найти частное решение этого уравнения, удовлетворяющее условию 1 5.
№2. Проверить, что заданная функция 6 является
′ 2 1, и найти
частное |
решение |
этого |
уравнения, |
удовлетворяющее |
условию |
2 4. |
что заданная функция 6 является общим |
||||
№ 3. |
Проверить, |
||||
решением дифференциального уравнения 0, |
и найти |
||||
частное |
решение |
этого |
уравнения, |
удовлетворяющее |
условию |
1 5. |
|
|
|
|
|
№ 4. |
Дано дифференциальное уравнение: ′ ′ ′ 0. |
||||
Определить порядок данного дифференциального уравнения и проверить, что функция 6 6 6 является общим решением этого дифференциального уравнения.
№ 5. Дано дифференциальное уравнение: ′′′ 3 ′′. Опреде-
лить порядок данного дифференциального уравнения и проверить, что функция 6= >? 6 является общим решением этого дифференциального уравнения.
№ 6. Проверить, что семейство гипербол >?? 1 является общим интегралом дифференциального уравнения ′ 1, и
найти частное решение этого уравнения, удовлетворяющее условию |
|||
2 1. |
|
семейство кривых 2 @ 6 является |
|
№ 7. Проверить, |
что |
||
общим интегралом дифференциального уравнения ′ |
, и найти |
||
частное решение |
этого |
уравнения, удовлетворяющее |
условию |
0 0. |
|
|
|
