
Linal_3
.pdf
Вопрос №1
Доказать, что линейная оболочка системы векторов является подпространством. Нахождение размерности подпространства.
Определение. Линейной оболочкой векторов 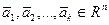 называется множество всевозможных линейных комбинаций этих векторов:
называется множество всевозможных линейных комбинаций этих векторов:
.
Теорема (свойства линейной оболочки).
1) 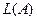 является подпространством
является подпространством 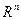 .
.
Доказательство.
1) 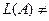 Ø, т.к.
Ø, т.к. 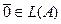 . Покажем, что множество
. Покажем, что множество 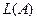 замкнуто относительно сложения векторов и умножения вектора на число.
замкнуто относительно сложения векторов и умножения вектора на число.
Пусть 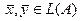 , т.е.
, т.е.  и
и 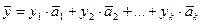 .
.
Тогда 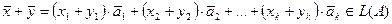 и
и 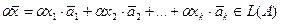 .
.
Вопрос №2
Доказать, что множество всех решений однородной системы линейных уравнений с п неизвестными образует подпространство в К "
Вопрос №3

Определить понятие единичного базиса в пространстве К п .
Единичный базис – это базис, состоящий из единичных векторов.
Вопрос №4,5,6
Определить сумму и пересечение подпространств.
Доказать, что сумма подпространств и пересечение подпространств есть подпространство.
Определить прямую сумму подпространств и прямое дополнение подпространства.
Пусть L и M - два подпространства пространства R.
Cуммой L+M называется множество векторов x+y, где x L и y M. Очевидно, что любая линейная комбинация векторов из L+M принадлежит L+M,

следовательно L+M является подпространством пространства R (может совпадать с пространством R).
Прямое дополнение линейного подпространства Определение прямого дополнения линейного подпространства
Пусть L′ – линейное подпространство линейного пространства L .
Прямое дополнение линейного подпространства L′ до линейного пространства L – это
линейное подпространство L′′ такое, что L = L′ L′′ .
Вопрос №7
Доказать теорему о единственном представлении произвольного вектора в виде суммы векторов, принадлежащих данному подпространству и его прямому дополнению.
Вопрос №8
Дать определение сюръективного, инъективного и биективного отображения. Обратное отображение.
Сюръективное это отображение при котором каждый элемент множества n имеет прообраз.

Инъективное отображение при котором каждый элемент из множества образов имеет единственный прообраз.
Биективное называется отображение являющаяся одновременно съерьективным и инъективным.
Обратное это отображение, в котором множества m и n меняется местами, при условии, что соответственно меняются направление.
Вопрос №9,10
Дать определение линейного оператора. Привести примеры.
Определить матрицу линейного оператора в данном базисе. Привести примеры.
Вопрос №11
Вывести формулу для нахождения образа вектора в данном базисе при заданной матрице оператора.
Вопрос№12

Дать определение образа и ядра оператора. Привести примеры.
Ядро линейного оператора это подмножества элементов образов, которой является нулевой вектор.
Образ линейного оператора это множества всех образов данного пространства при отображение в линейный оператор фи.
Вопрос №13
Доказать, что образ и ядро оператора являются подпространствами. Доказать теоремы о размерности образа и ядра данного оператора.
Вопрос№14
Доказать необходимые и достаточные условия для матрицы, ядра и образа биективного оператора.
У биективного оператора матрица невырожденная, ранг равен размерности. Ядро состоит из одного нулевого вектора. А образов является все подпространство.
Вопрос №15
Вывести формулу преобразования матрицы линейного оператора при переходе к новому базису.
Вопрос №16
Разбиение множества матриц одного порядка на классы подобных матриц. Неизменность величины определителя матрицы и величины следа матрицы в каждом классе подобных матриц.
Классы подобных это множества, которое потом разбивается на части. Матрицы, которые приводятся друг к другу, при помощи матрицы перехода ил используя формулы в 15 вопросе. Классы подобных матриц имеет один и тот же характеристических многочлен.
Вопрос№17,18
Определить действия с линейными операторами.
Произведение линейных операторов. Матрица произведения линейных операторов.
Пусть А и В – два линейных оператора, действующих из V в W. Суммой этих операторов назовем оператор А + В, определяемый равенством (А + В) 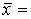 А
А 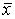 +В
+В  для любого
для любого  из V. Легко видеть, что сумма линейных операторов тоже будет линейным оператором.
из V. Легко видеть, что сумма линейных операторов тоже будет линейным оператором.
Сложение линейных операторов обладает, очевидно, следующими свойствами:
1.А + В = В +А.
2.(А +В) +Е = А + (В + Е).
3.А + О = А для любого А.
4.(–А) + А = О.
Произведением линейного оператора на скаляр α назовем оператор αА,
определяемый равенством 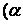 А)
А) 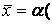 А
А 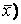 . Ясно, что αА – тоже линейный оператор.
. Ясно, что αА – тоже линейный оператор.
Для умножения линейного оператора на число справедливы, очевидно, следующие свойства:
1.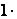 А = А; 0А = О; (–1)А= –А.
А = А; 0А = О; (–1)А= –А.
2.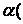 βА)
βА) 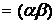 А.
А.
3. 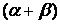 А =
А = 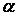 А + βА.
А + βА.
4. (А + В) = А + |
В. |
Обозначим через |
множество всех линейных операторов, действующих |
из V в W. |
|

Произведением линейных операторов А и В из |
называется |
оператор АВ, |
||
определяемый следующим образом: (А В) |
А(В |
для любого |
из V. |
Произведение |
линейных операторов тоже будет линейным оператором. |
|
|
|
|
Справедливы следующие свойства умножения линейных операторов:
1.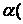 А В ) = (
А В ) = (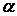 А )В.
А )В.
2.(А В ) Е = А (В Е ).
3.(А + В)Е = А Е + В Е , Е ( А + В) = Е А + Е В .
Умножение линейных операторов, вообще говоря, некоммутативно.
Вопрос №19
Условия существования обратного оператора. Матрица обратного оператора.
Линейный оператор В из 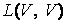 называется обратным для оператора А из
называется обратным для оператора А из 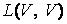 , если выполняется соотношение А В = В А = Е. Обратный оператор обычно обозначается как А–1. Для того чтобы линейный оператор А из
, если выполняется соотношение А В = В А = Е. Обратный оператор обычно обозначается как А–1. Для того чтобы линейный оператор А из 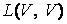 имел обратный, необходимо и достаточно, чтобы он был невырожденным.
имел обратный, необходимо и достаточно, чтобы он был невырожденным.
Вопрос№20
Дать определение собственного вектора и собственного значения линейного оператора. Привести примеры. Свойства собственных векторов данного оператора.
Свойства собственных векторов
Пусть : Xn → Xn — линейный оператор.

Все собственные векторы линейного оператора, соответствующие одному и тому же собственному значению, вместе с нулевым вектором образуют линейное пространство.
Собственные векторы линейного оператора, соответствующие различным собственным значениям, линейно независимы.
Если линейный оператор : Xn → Xn имеет n различных (вещественных) собственных значений, то собственные векторы, соответствующие этим собственным значениям, образуют базис в Xn . Такой базис называется собственным базисом линейного оператора
Матрица A линейного оператора : Xn → Xn в некотором базисе x1, x2, … , xn имеет диагональный вид тогда и только тогда, когда этот базис собственный, причем диагональные элементы этой матрицы — собственные значения оператора λ1, λ2, … , λn .
Вопрос №21
Доказать линейную независимость системы собственных векторов оператора, имеющих различные собственные значения.
Вопрос №22
Нахождение собственных векторов и значений линейного оператора (преобразования)
Для нахождения собственныхи собственныхвекторов значений линейного преобразования вещественного линейного проследуеттрансвавыполнить следующие действия.
1. Выбрать произвольный базислинейного пространстваи найти в этом базисе матрицупреобразования.

2.Составить характеристический многочлен преобразования .
3.Найти все различные действительные характеристическогокорни
уравнения |
. Комплексные (но не действительные) корни характ |
||
уравнения следуетотбросить (см. пункт 2. замечаний 9.4). |
|||
4. Для корня |
найти фундаментальную систему |
решений |
|
однородной системы уравнений |
, где |
. Для этого |
|
можно использовать либо алгоритм решения однородной системы, либо нахождения фундаментальнойматрицы.
5. Записать линейно независимые собственные векторы, отвечающиепреобразовани собственному значению
Для нахождения совокупности всех собственных векторов, отвечающих значению, образовать ненулевые линейные комбинации
где |
— произвольные постоянные, не равные нулю одноврем |
Повторить пункты 4, 5 для остальных собственныхлинейногозначений преобразования.
Вопрос№23
Характеристический многочлен линейного оператора. Доказать независимость характеристического многочлена от заданного базиса.
Вопрос№24
Доказать критерий диагонализируемости матрицы линейного оператора в К " .

КРИТЕРИЙ ДИАГОНАЛИЗИРУЕМОСТИ ОПЕРАТОРА:
Оператор φдиагонализируем тогда и только тогда, когда в пространстве Ln существует базис из собственных векторов оператора .
Этот базис составляется из базисов собственных подпространств.
Вопрос№25
Собственные подпространства линейного оператора. Случаи собственных подпространств в пространствах К 2 и в К 3 .
Вопрос№26
Геометрическая кратность собственного значения. Изложить условие диагонализируемости линейного оператора при известных алгебраических и геометрических кратностях собственных значений.
Геометрической кратностью собственного значения |
|
линейного оператора |
|
|||||
(преобразования) |
|
называется размерность собственного |
|
|||||
подпространства |
|
|
|
, соответствующего этому собственному значению. |
||||
Для того чтобы линейное преобразование (оператор) приводилось к диагональному виду, необходимо и достаточно, чтобы все корни характеристического многочлена являлись собственными значениями преобразования и геометрическая кратность каждого собственного значения была равна его алгебраической кратности.
Достаточность следует из теорем 9.5 и 9.6. Действительно, если для каждого из различных собственных значений 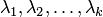 геометрическая кратность равна алгебраической
геометрическая кратность равна алгебраической
кратности, то  , т.е.
, т.е. 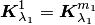 для всех
для всех 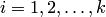 . Поэтому в равенстве (9.9) корневые подпространства можно заменить собственными: . Выбрав в каждом собственном подпространстве базис и объединив все эти базисы в единую систему, получим базис всего пространства, составленный из собственных векторов. Достаточность доказана. Необходимость доказывается путем приведения тех же рассуждений, но в обратном порядке.
. Поэтому в равенстве (9.9) корневые подпространства можно заменить собственными: . Выбрав в каждом собственном подпространстве базис и объединив все эти базисы в единую систему, получим базис всего пространства, составленный из собственных векторов. Достаточность доказана. Необходимость доказывается путем приведения тех же рассуждений, но в обратном порядке.
