
Linal_3
.pdf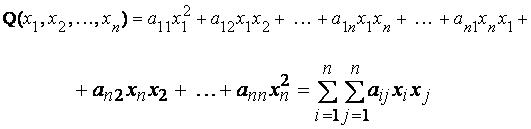
Квадратичной формой 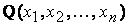 от n неизвестных
от n неизвестных 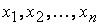 называется сумма, каждое слагаемое которой является или квадратом одного из этих неизвестных, или произведением двух разных неизвестных.
называется сумма, каждое слагаемое которой является или квадратом одного из этих неизвестных, или произведением двух разных неизвестных.
Обозначая коэффициент при 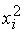 через
через 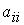 , а при произведении
, а при произведении 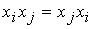
 – через
– через 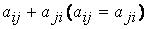 , квадратичную форму Q можно представить в виде
, квадратичную форму Q можно представить в виде
.
Симметричная матрица 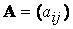 называется матрицей квадратичной формы Q.
называется матрицей квадратичной формы Q.

Вопрос№44
Приведение квадратичной формы к каноническому виду.
Теорема 6.1 о приведении квадратичной формы к каноническому виду. Любая квадратичная форма может быть приведена к каноническому виду при помощи некоторой линейной невырожденной замены переменных.
Конструктивное доказательство составляетэтойтеоремысодержание метода Лагр приведения квадратичной формы к каноническому виду.

Метод Лагранжа приведения квадратичной формы к каноническому виду
Для приведения квадратичнойпеременныхформы
к каноническому виду нужноследующиевыполнитьдействия.
1. Выбрать такую перемведущуюнную ),( которая входит в квадратичную фор второй и в первой степени одновременно (если в квадратичной форме переменной и с произведением этой переменной наи другуюперейтиперемек пунктуную
2.
Если в квадратичной форме нет ведущих переменных, то выбрать п произведение которых входит в квадратичную форму с отличным от ну перейти к п.3.
Если в квадратичной форме отсутствуютазличныхпроизведеременных,ния то никаких преобразований делать не надо, так как она уже имеет кано
2.По ведущей переменной выделить полный квадрат: собрать в квад члены с ведущей переменной, дополнить сумму этихвадратачленов до полног (разумеется, добавленные члены нужно также и вычесть, чтобы не из Получим сумму полного квадрата некоторой линейной формы (в котору переменная) и квадратичной формы, в которую ведущая переменная не замену переменных: линейную форму, содержащую ведущую переменную, новых переменных, а все старые переменные, за исключением ведущей соответствующие новые. Продолжить преобразования с пункта 1.
3.Выбранную пару переменныхитьзамна разность и сумму двух новых пер остальные старые переменные принять за соответствующие новые пере произведение пары выбранных переменных преобразуется к разности к
переменных, т.е. в новой формеквадратичнойбудут квадраты переменных с отли от нуля коэффициентами. Продолжить преобразования новой квадратич
1.
Идея метода Лагранжа состоит в том, что прием, используемый в квадрата), исключает однуизпеременнуючисла ведущих. Например, если —перемен ведущая (т.е. и хотя бы один из коэффициентов отличен от

нуля), то выделяем полный квадрат по(собираемпе еменнойвсе членыи дополняемс их сумму до полного квадрата):
Выражение, стоящее атныхвквадрскобках, есть полный квадрат. Поэтому
где
— квадратичная форма, в которую не входит ведущая
переменная |
— линейная форма, содержащая ведущую |
переменную. Обозначим |
, |
или, что то же самое, сделаем линейную замену переменных: |
|
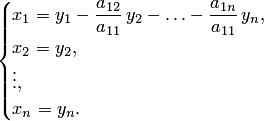 (6.12)
(6.12)
Тогда данная квадратичная форма преобразуется к
виду |
. |
Заметим, что в результате этого преобразования все члены, соде переменную в первой и второй степени, заменены квадратом одной. нов В дальнейших преобразованияхная переменухуже никогда не будет ведущей.
Многократно применяя этот прием, исключаем одну за другой все получая тем самым канонический вид квадратичной формы. Однако выд квадрата невозможно, если в квадратичной форме вообще отсутствуют

переменных. В этом случае применяется способ, описанный в п.3, кото с квадратами переменных.
Например, в п. 1 выделена пара ипеременных, произведение которых входит квадратичную форму с отличным от нуля коэффициентом.Тогда нужносделать замену переменных
(6.13)
При этом получим новую квадратичную, вформукоторой появятся квадраты переменных с отличными от нуля коэффициентами, так как в результа член преобразуется к виду
а других членов новойсквадратичной форме не будет.
Заметим, что при помощи метода Лагранжа не только находится ка определяется искомая невырожденная замена переменных. В самом дел переменных (6.12), (6.13), которые производяэтосялинейныев п.2, 3заменылгоритмс матрицами
(6.14)
Определители матриц отличны от нуля . Следовательно, эт замены переменных невырожденные. Выполняя п.2, 3 алгоритма, можно используемых замен переменных. В результате порядкеихперемножениянахождения)(в получается матрица искомой замены (согласно свойству 2 линейных з


Вопрос№45
Изложить классификацию кривых и поверхностей второго порядка в соответствии с видом квадратичной формы


Вопрос№46
Доказать закон инерции квадратичных форм.

Доказательство: Пусть имеются 2-а базиса, в которых квадратичная форма A(X,X) принимает нормальный вид: 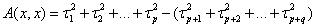 в базисе
в базисе 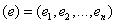
 в базисе
в базисе  .
.
Здесь полагаем, что 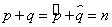 т. е. в этих 2-х базисах (и во всех остальных!) нулевые коэффициенты в нормальном виде квадратичной формы отсутствуют. Очевидно, что для
т. е. в этих 2-х базисах (и во всех остальных!) нулевые коэффициенты в нормальном виде квадратичной формы отсутствуют. Очевидно, что для
доказательства этой теоремы достаточно предположить, что 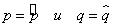 .
.
Будем доказывать методом от противного, т. е. предполагаем, что 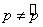 ; пусть,
; пусть,
например, 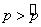 .
.
Рассмотрим следующие пространства: |
и |
. |
||
Очевидно, что |
|
|
. Применим формулу |
|
Грассмана: |
|
|
|
, т. е. |
пространство |
- непустое, следовательно, существует хотя бы один ненулевой |
|||
элемент |
, т. к. |
, то |
. |
|
Точно также |
, поэтому |
|
. Т. к. |
, то с |
одной стороны |
|
|
, с другой |
|
