2519

Введение. В работе рассматривается соответствие метрической геометрии эллиптической плоскости и линейчатого пространства R3(l), представляемого как многообразие прямых расширенного трехмерного евклидова пространства R3+. В высшей геометрии исследования пространства R3(l) выполняются на принципах перенесения [1], основанных на отображениях пространства R3(l) на квадрику

Плюккера Q42 P5или на единичную сферу

S2(ω) в дуальном трехмерном евклидовом пространстве R3(ω). Последний случай соответствует принципу перенесения КотельниковаШтуди [2, 3, 4, 5]. Этот принцип допускает развитие, в результате которого появляется возможность конструктивно-метрического моделирования пространства R3(l) на эллиптических плоскостях – комплексной и дуальной [6]. В настоящей работе в направлении дальнейшего исследования указанных плоскостных моделей рассматривается метрический аспект моделирования - соответствие метрических геометрий комплексной эллиптической плоскости и пространства R3(l).

Соответствие метрических геометрий

В высшей геометрии известно, что связка прямых и плоскостей T2, концентричная с ней сфера S2 с отождествленными диаметрально противоположными точками, плоскость R2S, касательная к сфере – это гомеоморфно соответственные модели комплексной эллиптической плоскости в пространстве R3+, допускающей интерпретацию метризованной проективной плоскости [3,7]. Последнее означает, что как расстояние между двумя точками, так и угол между двумя прямыми этой плоскости могут быть формульно выражены в евклидовой координатной и в проективной форме [3,7]. Изотропный конус K2 связки индуцирует на плоскости R2S эллиптическую метрику, оп-

ределяемую абсолютом kR2 K2 R2S , представляющим собой нераспадающуюся мни-

мую конику. Линия k2 K2 , где - несобственная плоскость пространства R3+, является, как известно, абсолютом этого пространства. Все множество изотропных прямых пространства R3+, проходящих через точки

абсолюта k 2, образует специальный квадратичный комплекс KM2, конусом которого является изотропный конус K2. Поскольку абсолют

k 2 представляет собой образ абсолюта kR2 и

комплекса KM2 на плоскости , то KM2 естественно принять в качестве абсолюта пространства R3(l). Соответствие абсолютов kR2 и KM2

по абсолюту k 2 приводит к соответствию метрических структур плоскости R2S и про-

странства R3(l): M(R2S ) M(R3(l)). Между пространством R3(l) и дуальной плоскостью

R2S( ) касательной к единичной дуальной

сфере S2(ω), существует гомеоморфное соответствие, которое позволяет продолжить указанное соответствие метрических структур до

абсолютом которой является дуальный образ kR2( ) абсолюта KM2 [8]. В этом соответствии

расстоянию δ<( /2)r между двумя точками Y(yk) и Z(zk) эллиптической плоскости R2S, выраженному взаимосвязанными формулами:

где r – радиус кривизны плоскости R2S; I1, I2 – точки пересечения прямой YZ с абсолютом kR2, - этому расстоянию соответствует дуальное расстояние 0 1 двух точек y(Yk)

и z(Zk) в дуальной плоскости R2S( ) , опреде-

ляемое соответствующими взаимосвязанными дуальными формулами:

гдеcos cos 0 1sin 0 ;

ln ln 0 ( 1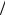 0); k = 1,2,3; ω2=0, ω –

множитель Клиффорда; Yk y0k y1k; Zk z0k z1k;i1, i2 – дуальные изотропные точки пересечения линий yz kR2( ) . Веще-

ственной интерпретацией дуальных точек y и z и их дуального расстояния в плоскости

R2S( ) является в пространстве R3(l) пара скрещивающихся направленных прямых с комплексным углом 0 1, где δ0 и δ1

– кратчайшее расстояние и угол между ними. Из соответствия метрических структур (1) следует, что полярности точки A(ak) в плоскости R2S относительно абсолюта kR2, приводящей к уравнению прямой ∑akxk=0 – поляры этой точки, соответствует в плоскости

R2S( ) полярность дуальной точки a(Ak) отно-

сительно абсолюта kR2( ) , приводящей к

уравнению дуальной прямой ∑AkXk=0, вещественной интерпретацией которой в пространстве R3(l) является щетка - линейчатая “поляра” прямой, представляющей собой вещественный образ точки a(Ak), относительно абсолюта KM2. Из полярности относительно абсолюта kR2 плоскости R2S, приводящей к евклидовым координатным и проективным формульным выражениям угла между двумя пря-

мыми a(ak) и b(bk):

где i1, i2 – изотропные прямые, проходящие через точку a∩b, - из этой полярности, на основании соответствия (1), следует полярность

относительно абсолюта kR2( ) плоскости

R2S( ) , приводящей к соответствующим фор-

мулам дуального угла двух дуальных прямых

∑AkXk=0 и ∑BkXk=0, а именно:

cos AkBk; 1 ln(abi1i2), 2i

где 0 1; k = 1,2,3; ω2=0, a(Ak), b(Bk), i1, i2 – соответственно пара дуальных вещественных и пара дуальных изотропных прямых,

которым в пространстве R3(l) соответствуют пара вещественных и пара изотропных щеток первого порядка в составе щетки второго по-

рядка. Последней в плоскости R2S( ) соответ-

ствует дуальный образ – пучок дуальных прямых, которому принадлежат прямые a(Ak), b(Bk), i1, i2. Группа преобразований метрической геометрии плоскости R2S представляет собой группу автоморфизмов относительно ее абсолюта kR2, которые определяются преобразованиями сферы S2 с неподвижным центром O, касательной к R2S. Такими преобразованиями сферы являются вращения ее относительно центра O и отражения ее относительно диаметральной плоскости. Преобразования сферы индуцируют соответствующие преобразования плоскости R2S, формульное представление которых имеет вид:

где i, j,k=1,2,3; i≠j; ρ . Поскольку координаты вещественных точек плоскости R2S удовле-

xi2 0плоскости R2S относительно преоб-

разований (2). Простое вращение сферы S2 относительно ее центра O есть вращение относительно прямой, проходящей через центр. Пусть этой прямой соответствует точка OR(0,0,r) в плоскости R2S. Из неподвижности центра OR и инвариантности (неподвижности) абсолюта kR2 относительно преобразований

(2) следует неподвижность поляры x3=0 центра OR в полярности относительно kR2. Учитывая это, а также ограничения для коэффициентов в уравнениях (2), можно получить в матричном виде уравнения преобразований движения и отражения относительно прямой в плоскости R2S:

X aik X; aik 1; X bik X; bik 1.

При этом отражение относительно прямой рассматривается как полученное в результате непрерывного движения – вращения относительно центра – полюса этой прямой [7]. Из уравнений (2) преобразований и ограничений на их коэффициенты следует, что автоморфизмы плоскости R2S относительно ее абсолюта образуют трехпараметрическую группу.

Из соответствия метрических структур (1) следует соответствие между группой автоморфизмов (2) плоскости R2S и группой автоморфизмов дуальной эллиптической плоско-

сти R2(S ) относительно ее абсолюта kR2( )

с вещественной интерпретацией последней в линейчатом пространстве R3(l). Группа дуальных вращений единичной дуальной сферы S2(ω) относительно ее центра описывается уравнениями:

Xi Aik Xk; Aik 0; (Xi)2 Xi2 , (3) k

где i, k =1,2,3 и девять дуальных коэффициентов удовлетворяют шести дуальным уравнениям

Aik Aij (1 при k=j, 0 при k≠j). (4) i

Преобразования (3) сферы S2(ω) приводят к соответствующим преобразованиям плоско-

сти R2(S ) :

где ρ≠0 - дуальный коэффициент. Эти преобразования образуют группу автоморфизмов

относительно абсолюта kR2( ) . Автоморфиз-

мам (5), а следовательно и (3), в пространстве R3(l) соответствует шестипараметрическая группа винтовых движений, оставляющих неизменным абсолют KM2 этого пространства. Действительно. Неподвижной оси v винтового

движения соответствует ее точка V на несобственной плоскости пространства R3+.

Поляра v точки V относительно абсолюта

k 2 есть множество несобственных точек прямых щетки с осью v. В винтовом движении с осью v прямые линии щетки перемещаются внутри щетки, что приводит к перемещению по-

ляр этих точек в пучке (V ). Угловому переме-

щению поляр пучка, пересекающих абсолют k 2, соответствует внутреннее перемещение точек абсолюта. Следовательно, винтовому движению с осью v соответствует вращение в плос-

кости , инвариантными фигурами которого являются: абсолют k 2, центр вращения V и

поляра v центра. Инвариантности абсолюта

k 2 относительно вращения в плоскости взаимно однозначно соответствует инвариантность абсолюта KM2 пространства R3(l) относительно винтового движения, поскольку

коника k 2, будучи направляющей линией

специального квадратичного комплекса изотропных прямых KM2, полностью его определяет. Дуальная эллиптическая плоскость

R2S( ) , как и плоскость R2S, допускает интер-

претацию дуальной проективной плоскости [8]. В этой связи гомеоморфизм

R3(l) R2(S ) и соответствия метрических структур (1) позволяют утверждать о существовании конструктивно-метрического соответствия (КМС) между плоскостью R2S, простран-

ством R3(l) и плоскостью R2(S ) . КМС позволя-

ет рассматривать каждую из этих плоскостей как определенную модель пространства R3(l). Рассмотрим проявления КМС моделей на полярном соответствии относительно мнимого абсолюта kR2 в плоскости R2S. На рисунке 1 треугольник M0 N0 E0 является автополярным, при этом расстояние между любой вершиной и любой точкой противоположной стороны равно ( /2)r и сами точки называются ортогональными. Такими являются точки M0 и N0. Для ортогональных точек характерно (M0 N0 I1 I2)= -1. На рисунке 2 приведено изображение соответствующего полярного соответствия в плоскости

R2(S ) относительно ее мнимого дуального

абсолюта kR2( ) . При этом m0(ω), n0(ω), e0(ω),

i1(ω), i2(ω) – дуальные точки, являющиеся образами прямых пространства R3(l), причем m0(ω), n0(ω), e0(ω) –образы осей соответствующих щеток. Образами этих прямых на плоскости R2S являются точки. m1(ω), n1(ω), e1(ω) – дуальные прямые, каждая из которых является

образом множества 2 прямых линий щетки первого порядка в R3(l) и каждой из которых в плоскости R2S соответствует прямая. Из КМС моделей следует, что образом щетки без ее

оси, как множества 2 прямых, ортогонально пересекающих ось щетки, на каждой из плос-

костей R2S и R2(S ) является прямая. Образом щетки с включенной в нее осью на каждой из плоскостей R2S и R2S( ) является пара полярно

соответственных элементов: точка – полюс и прямая – поляра в абсолютной полярности.

Рис.1 Полярное соответствие в плоскости R2S

Рис. 3 Линейчатый автополярный треугольник m0n0l0 в R3(l)

Рис. 5. Ортогональная проекция n/ прямой n на щетке m0(m1)

На рисунке 3 представлена конструктивная интерпретация автополярного линейчатого треугольника, образами которого на плоскости R2S является треугольник M0 N0 E0, на плоско-

сти R2S( ) - дуальный треугольник m0(ω) n0(ω)

e0(ω). При этом соответствие образов на R2S( )

и прообразов в R3(l) имеет следующий вид:

m0(ω) m0(m1), n0(ω) n0(n1); e0(ω) e0(e1); m1(ω) m1, n1(ω) n1, e1(ω) e1, где m0(m1),

n0(n1), e0(e1) – оси соответствующих щеток m1, n1, e1 первого порядка. Тонированная точка на изображении линейчатой интерпретации означает ортогональность пересекающихся в ней прямых. Рассмотрим КМС ортогональных

Рис. 2. Полярное соответствие в плоскости R2S( )

Рис. 4 Ортогональная проекция N/ точки N на прямой m

проекций на моделях пространства R3(l). Пусть на рисунке 4 заданы в плоскости R2S точка N и прямая m. Требуется определить основание перпендикуляра, опущенного из точки на прямую. Для этого вначале определим полюс M0 заданной прямой m, затем проведем прямую e(N,M0) и определим точку N/=e∩m, которая и будет решением. Действительно. Прямая e по построению ортогональна прямой m, значит точка N e ортогональна точке N/=e∩m. Минуя образное представление

в плоскости R2S( ) полученной конструкции в

плоскости R2S, выполним, как показано на рисунке 5, ее линейчатую интерпретацию в пространстве R3(l). Полученная линейчатая конструкция и ее прообраз в плоскости R2S имеют

следующее соответствие элементов: N n, m m1, M0 m0, e e1, E0 e0, N/ n/. При этом n/ e0(e1), n/ m0(m1). Рассмотрим свойство срединных перпендикуляров треугольника в плоскости R2S и определим аналог этого свойства в пространстве R3(l) посредством плоско-

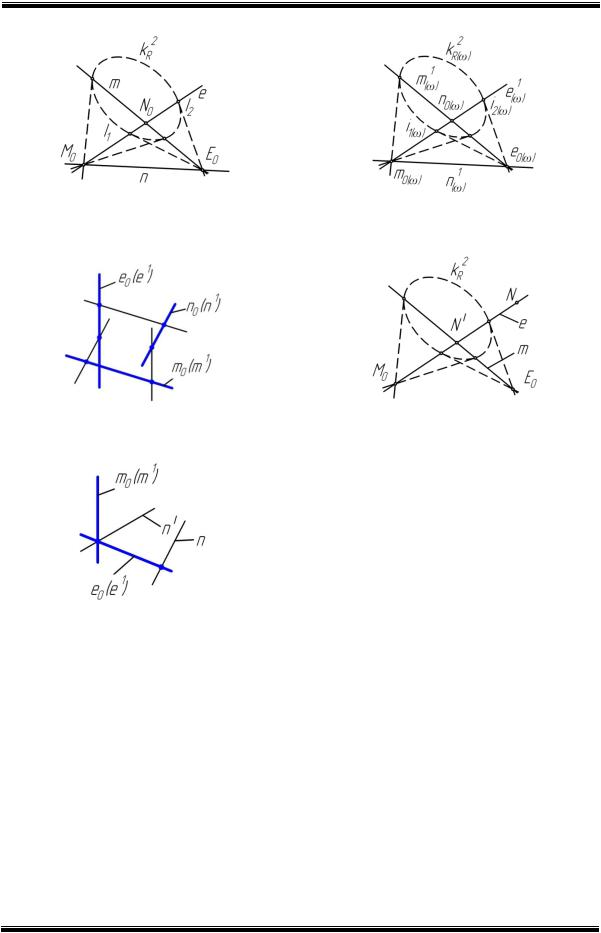
сти R2S( ) . На рисунке 6 в плоскости R2S оп-

ределены три различные точки X,Y,Z такие, что ни одна из них не ортогональна двум другим. Как известно, три точки эллиптической

Рис. 6. Треугольник XYZ в плоскости R2S

плоскости определяют четыре треугольника с вершинами в этих точках [7]. Введя дополнительное условие, например, длина каждой стороны меньше ( /2)r, получаем один треугольник XYZ. В треугольнике эллиптической плоскости срединные перпендикуляры, проходящие через стороны треугольника, пересекаются в одной точке [7]. На рисунке 7 изо-

бражен выполненный в плоскости R2S( ) ду-

альный образ рассматриваемой конструкции в плоскости R2S на основании КМС рассматри-

ваемых моделей R2S и R2(S ) пространства

R3(l). Следующим шагом выполним линейчатую интерпретацию в пространстве R3(l), представленную на рисунке 8, полученной

дуальной конструкции в плоскости R2(S ) .

Рис. 7. Треугольник x(ω)y(ω)z(ω)

в плоскости R2(S )

На изображении линейчатой интерпретации тонированная точка означает попарную ортогональность пересекающихся в ней прямых пространства. Для пространства R3(l) имеет место следующее предложение: срединные щетки

n01(n11), n02(n21), n03(n31), проходящие через срединные прямые m1, m2, m3 щеток – сторон

a0(axz1), b0(bxy1), c0(cyz1) дуального треугольника xyz, имеют общую прямую n. Установленное для эллиптической плоскости R2S понятие конгруэнтности [9], может быть на основе КМС перенесено в дуальную эллиптическую плоскость

Рис. 8. Линейчатый треугольник xyz в пространст-

ве R3(l)

R2S( ) с последующей интерпретацией в

линейчатом пространстве R3(l). Отрезку прямой и углу двух прямых в плоскости R2S соответствуют в пространстве R3(l) понятия линейчатого отрезка и линейчатого угла [10]. Под линейчатым отрезком понимается отсек щетки первого порядка, ограниченный пучками ее прямых, с выделенными двумя прямыми по одной в каждом граничном пучке. Следовательно, линейчатый отрезок определяется двумя прямыми линиями щетки и ее осью. Под линейчатым углом понимается пространственная фигура, образованная полуотсеками двух щеток с обшей прямой, принадлежащей граничным пучкам полуотсеков. Таким образом, линейчатый угол определяется осями двух щеток и их общей прямой. Очевидно, он является двойственной фигурой по отношению к линейчатому отрезку, что следует из двойственности прямой линии и щетки в пространстве R3(l), которой соответствует двойственность точки и прямой в эллиптической плоскости [6,7] - двойственность как в отношении конструктивной принадлежности, так и в отношении эллиптического мероопределения, когда из формулы расстояния следует формула угла. КМС позволяет ввести понятие конгруэнтности для линейчатых отрезков и линейчатых углов во множестве собственных прямых пространства R3(l). Так, два линейчатых отрезка считаются конгруэнтными, если существует движение в пространстве R3(l), в результате которого происходит наложение этих отрезков, при этом выделенные граничные прямые линии одного линейчатого отрезка налагаются соответственно на выделенные граничные прямые другого [10]. Аналогичным образом определяется конгруэнтность линейчатых углов.

Заключение. На основании вышеизложенного можно сделать вывод о том, что кон- структивно-метрическое соответствие линейчатого пространства и его моделей - комплексной и дуальной эллиптических плоскостей, приводит к соответствию метрических геометрий пространства и его моделей. Это позволяет выполнять решения различных теоретических и прикладных задач метрической геометрии линейчатого пространства на его эллиптических плоскостных моделях [6, 8,11,12]. В соответствии метрических геометрий трехпараметрической группе движений комплексной эллиптической плоскости соответствует трех дуальнопараметрическая группа движений дуальной эллиптической плоскости и шестипараметрическая группа движений линейчатого пространства. Поскольку связная группа движений первого рода евклидова трехмерного пространства шестипараметрична, то можно сделать вывод о существовании изоморфизма между группами движений линейчатого пространства, дуальной эллиптической плоскости и евклидова пространства.

Библиографический список

1.Клейн, Ф. Высшая геометрия / Ф. Клейн. – М.; Л.: ОНТИ, 1939. – 400с.

2.Диментберг, Ф. М. Теория винтов и её приложения / Ф. М. Диментберг. – М.: Наука, 1978. – 328 с.

3.Розенфельд, Б. А. Неевклидовы геометрии / Б. А. Розенфельд. – М.: Гос. изд-во техн.-теор. лит., 1955. – 744 с.

4.Норден, А. П. О некоторых возможных направлениях развития линейчатой геометрии / А. П.

Норден // Ученые записки Казанского ун-та, 1963.

–Вып. 123, кн. 1. – С. 145-151.

5.Pottmann, H. Computational Line Geometry / H. Pottmann, J. Wallner. – Berlin: Springer Verlag, Heidelberg, 2001. –565p.

6.Панчук, К. Л. Конструктивно-метрическое моделирование линейчатого пространства / К. Л. Панчук, В. Я. Волков // Вестник КузГТУ. – 2007. - №6. – С. 55-58.

7.Клейн, Ф. Неевклидова геометрия / Ф. Клейн.

–М.; Л.: ОНТИ НКТП СССР, 1935. – 355 с.

8.Панчук, К. Л. Моделирование линейчатого пространства дуальной эллиптической плоскостью / К. Л. Панчук, В. Я. Волков // Вестник СибГАУ им

акад. М.Ф. Решетнева. – Красноярск, 2007. – Вып. 4(17). - С. 54-56.

9.Ефимов, Н. В. Высшая геометрия / Н. В. Ефимов. – М.: Наука, 1971. – 576 с.

10.Панчук, К. Л. Геометрическое моделирование линейчатого метрического пространства в инженерной геометрии и ее приложениях: автореф. дис. … д-ра техн. наук: 05.01.01/ К. Л. Панчук. - Омск: ОмГТУ, 2009. – 40с. – Библиогр.: с. 39-40.

11.Панчук, К. Л. Линейчатые модели эллиптической прямой / К. Л. Панчук, В. Я. Волков // Вестник КузГТУ. –2007. - №6. - С. 52-54.

12.Панчук, К.Л. Уравнение Эйлера-Савари для эллиптической плоскости и его интерпретация в линейчатом пространстве / К. Л. Панчук // Омский научный вестник. – 2008. – №1(64). – С. 31-34.

ABOUT METRIC GEOMETRY OF AN ELLIPTIC PLANE AND LINE SPACE

K. L. Panchuk, V.Y. Volkov

Results of research on a conformity establishment between metric geometry of an elliptic plane and line spaces are presented and proved. Examples of display of this conformity are considered.

Are noted its theoretical and practical utility.

Панчук Константин Леонидович, доктор технических наук, доцент, профессор кафедры ”Начертательная геометрия, инженерная и компьютерная графика” Омского государственного технического университета. Основное направление научных исследований: геометрическое моделирование линейчатого метрического пространства и его технические приложения. Имеет около 100 опубликованных научных статей, учебных пособий, авторских свидетельств.

E-mail: Panchuk_KL@mail.ru.

Волков Владимир Яковлевич, доктор технических наук, профессор, заведующий кафедрой "Начертательная геометрия, инженерная и машинная графика" Сибирской государственной авто- мобильно-дорожной академии. Основное направление научных исследований: многомерная исчислительная геометрия. Имеет более 200 опубликованных монографий, учебников, учебных пособий, научных статей, патентов, авторских сви-

детельств. E-mail: volkov_vy39@mail.ru.

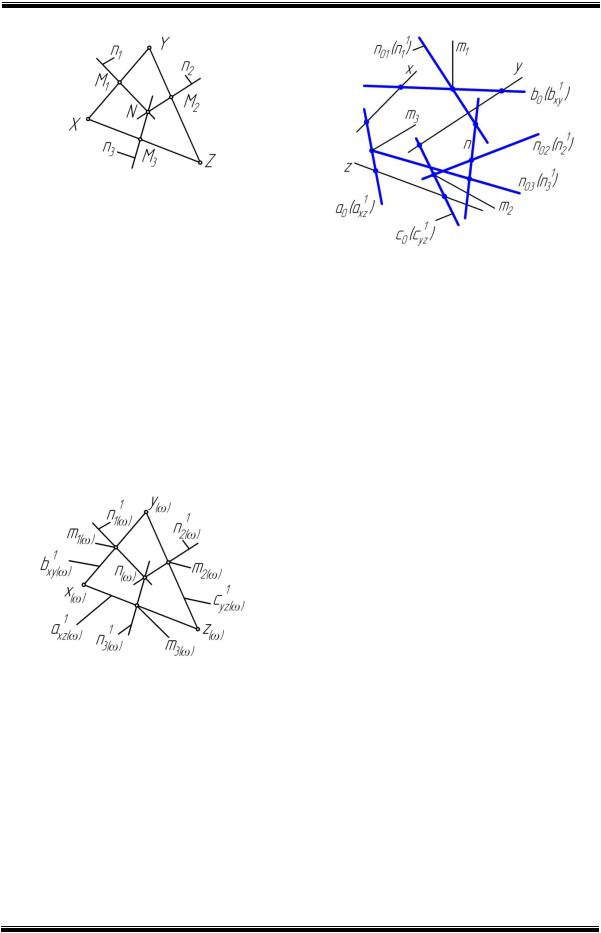
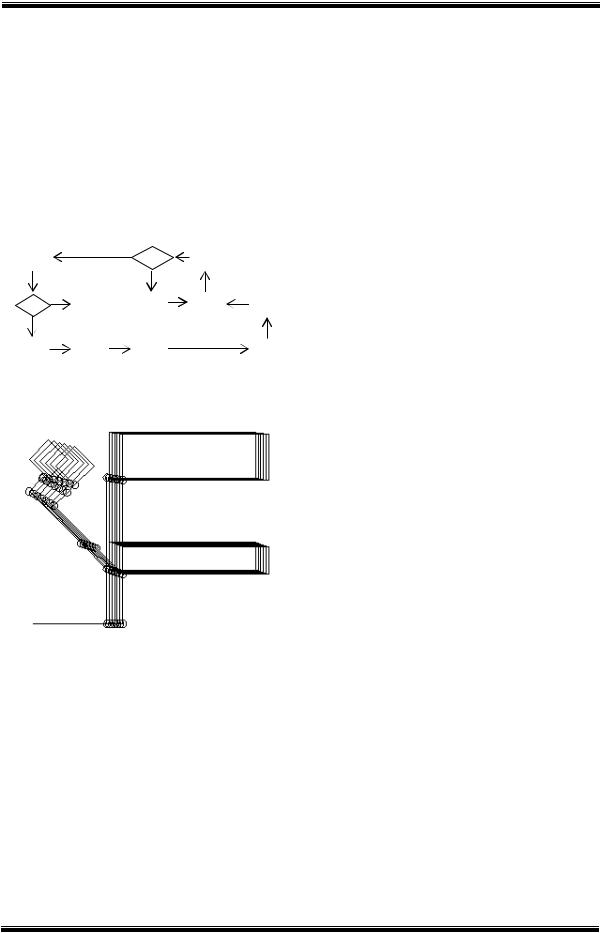
При задании различных геометрических значений переменных параметрической 3-D модели режущего инструмента и получении на основе ее плоского чертежа могут возникнуть проблемы, связанные с тем, что произойдет выход отдельных изображений видов или сечений за пределы границ чертежа или их взаимное пересечение [1]. Как правило, этот чертеж редактируется пользователем вручную, на что уходит некоторое количество времени. Поэтому актуальной задачей является разработка программ, которые автоматизированным способом позволяют наиболее оптимально располагать фрагменты изображений видов, сечений, текстов технических требований и др. На рисунке 1

представлены изображения двух видов и сечения резца.

При создании плоского чертежа на основе параметрической 3-D модели точки вставки видов и сечения P1, P2 и P3 указывают таким образом, чтобы расстояния до рамки чертежа, между видами и сечениями было задано с некоторым запасом. Данные расстояния на рисунке 1 определяют параметры q1/ , q2/ , q3/ , q4/ и

т.д. В заданных пределах могут изменяться положения базовых точек O2, O3, O4 и O5 фрагментов изображений, которые находятся обобщенными координатами q1, q2, … q5.

q1 q1/

q2

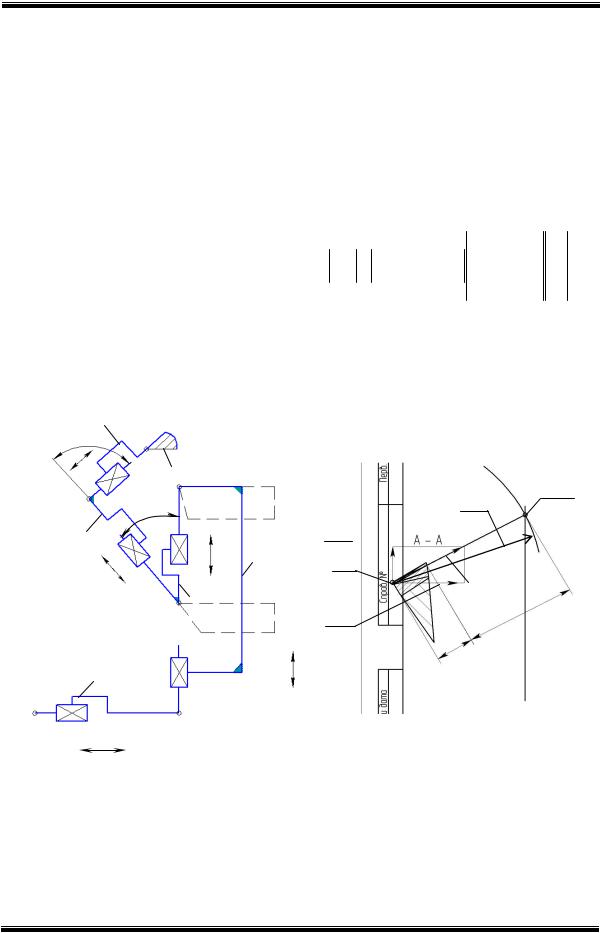
Положение указанных точек определяется с помощью функций доступа к примитивам. При этом первоначально параметрическую 3- D модель создают по средним значениям переменных определенного кода инструмента. Проводя аналогию с методами синтеза малых движений механизмов роботов, системы O1, O2, … O5 определяют положения видов, каждый из которых смещается вместе со звеньями 1, 2, … 5 открытой кинематической цепи с помощью реализации приращений ∆q1, ∆q2, …

∆q5 (рис. 2а).

На рисунке 2б представлен случай, когда точка O5 сечения А-А выступает за рамку чертежа. Для корректировки положения сечения необходимо рассчитать новые положения базовых точек O1, O2, … O5 с помощью приращений ∆q1, ∆q2,…, ∆q5 при которых точка O5 сместится по направлению прямой заданной точками O5, O5/ (см. рис. 2б). Положение точки

O5/ вычисляется пересечением окружности с центром O5 и радиусом RO5 с вертикальной

прямой l O2, l O3. Значение параметра RO5 определяется длиной lс и заданным минимальным удалением lб сечением от прямой l. Смещение базовой точки O5 определяется приращением ∆SO5. Данное приращение находится суммой (см. рис. 2б):

Из теории управления манипуляционными роботами известна зависимость между приращениями ∆xO5, ∆yO5 и ∆q1, ∆q2, … ∆q5:

a1 0 ... 0 q1

xO5 J11 J12 ... J15 0 a2 ... 0 q2 . (2)

0 0 ... a5 q5

O5/

RO5

∆yO5

O5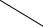

∆SO5

lб

∆xO5

lс

l

б

где J11, …, J25 – определяют коэффициенты матрицы частных передаточных отношений, а1, …, а5 – весовые значения приращений ∆q1, …, ∆q5 [2]. При этом, чем меньше значение весового коэффициента, тем больше происходит изменение обобщенной координаты. Весовые коэффициенты аi изменяются в за-

висимости от значений q1/ , … q5/ . Например если q1/ принимает минимальное значение,

тогда коэффициент а1 увеличивается до значения близкого к единице. Для первого варианта итерационного поиска значения аi принимаются в соответствии с заранее заданными приоритетами. Так если за пределы рамки чертежа выступает сечение, то наименьшее значение принимает коэффициент а4 и а5. Если соответственно выступает за верхнюю рамку чертежа вид спереди, то наименьшее значение принимает коэффициент а2.. Далее вычисляется новое положение видов и сечений. Пусть при итерационном поиске точка O2 приближается к граничной прямой l/ в этом случае значение весового коэффициента вычисляется по формуле:

гдеql/1- определяет удаление точки O2 от

граничной прямой l/. Другие значения коэффициентов аi рассчитываются аналогичным образом. При этом на начальном этапе значения весовых коэффициентов принимается такими, что наибольшее изменение происходит у четвертой и пятой обобщенных координат.

Для вычисления приращений ∆qi удовлетворяющих условию:

ài qi 2 min (5)

необходимо к линейной системе (3) добавить три линейных уравнения (6) Данные уравнения имеют следующий вид:

Коэффициенты данных уравнений J31, .., J55 находятся на основе использования условия:

Таким образом, для определения коэффициентов первого уравнения соотношений (6) необходимо в системе (7) в качестве неизвестных принять коэффициенты J31, …, J35. При

этом нужно произвольно задать p коэффициентов J3i и решить линейную систему уравнений (7): где p= r - n, r – размерность вектора

приращений ∆SO5 (∆xO5, ∆yO5), n – размерность вектора ∆Q (∆q1, ∆q2,…, ∆q5) приращений

обобщенных координат.

Совместное решение уравнений (2) и (6) позволяет в пространстве приращений ∆qi найти точку удовлетворяющую критерию (5).

Пусть при некотором шаге расчетов вектора приращений ∆Q наружные контуры некоторых видов или сечений пересекаются. Тогда необходимо вектор приращений ∆Q вычислить по формуле:

p

∆Q = ∆QM + ki ∙ m ∙∆Qli, (8) i 1

где ∆QM – вектор, определяющий положение точки MQ пространства приращений ∆qi; ∆Qli – орты, которые задают направления осей репера р-плоскости, которая задана уравнением (3), k1, …, ki – параметры, определяющие координаты точки N a 4 в указанном репе-

ре; m – длина единичного отрезка репера. Вычисление различных значений векторов

∆Q и следовательно положений систем O1, O2, … O5 происходит до тех пор пока граничные многоугольники видов или сечений и рамки чертежа будут располагаться на заданном расстоянии друг друга.

Для расчета значений приращений ∆qi необходимо задать геометрическую модель расчета положения систем координат связанных с фрагментами изображений представленных на рисунке 2а [2]. Данную модель, как известно, определяют массивы qi, li, lsm и nkod. Указанные массивы соответственно задают значения обобщенных координат qi, длины звеньев механизма li, смещения вдоль осей систем координат lsm и коды преобразований систем координат nkod. Значения массивов для кинематической цепи представленной на рисунке 2а представлены в таблице 1. Угол α1 определяется углом U1 (см.рис. 1).

Блок-схема расчета алгоритма положения фрагментов изображений представлена на рисунке 3.

На рисунке приняты следующие обозначения: 1 определение положения систем координат O1, O2, … O5; 2 существует ли пересечение фрагментов изображений.

Таблица 1 – Значения массивов определяющих геометрическую модель положения систем координат

Рис. 3. Алгоритм корректировки положения фрагментов изображений

Рис. 4. Результаты расчета приращений обобщенных координат, определяющих положения габаритных прямоугольников фрагментов изображений чертежа

Определение принадлежности точек контуров видов и сечений запретным зонам; 3 определение приращения ∆SO5 (1); 4 вычисление матрицы частных передаточных отношений; 5 число итераций равно единице; 6вычисление аi (4); 7 – вычисление уравнений гиперплоскости Φ (6 7); 8 – вычисление вектора ∆Q (8); 9 – qi+1 = qi +∆qi; 10 - опреде-

ление пересечений фрагментов изображений; 11 – изменение ki; 12 – конец.

Таким образом, вычисляя новое положение систем координат O1, O2, … O5 и определяя взаимное пересечение наружных контуров видов и сечений с помощью итерационного поиска находим такое положение, при котором точка O5 не выступает за пределы рамки чертежа. При этом на каждом шаге вычисляются новые значения коэффициентов аi.

На рис. 4 представлены результаты расчета приращений обобщенных координат с целью смещения габаритных прямоугольников фрагментов изображений.

Библиографический список

1.Шмуленкова, Е. Е. Автоматизированный способ оценки и корректировки положения фрагментов изображений металлорежущего инструмента // Вестник СибАДИ. 2010. № 3 (17). С. 58–64.

2.Притыкин Ф. Н. Геометрическое моделирование при решении задач робототехники: учеб. пособие. Омск, 1998. 69 с.

DECISION OF THE PROBLEM OF OPTIMUM ACCOMODATION FRAGMENT SCENES OF THE DRAWINGS CUTTING INSTRUMENT, DERIVED ON THE BASIS OF

3-D MODELSPARAMETRIC

E.E. Shmulenkova

Abstract. In article is considered automated optimum allocation way of scenes fragment on drawing metal-cutting instrument. The Mutual positions fragment scenes are defined by variables monitoring of the generalized coordinates. Under sequential searchare defined incrementations of the generalized coordinates with provision for importances of weighting coefficients.

Шмуленкова Елена Евгеньевна - аспирантка кафедры «Начертательная геометрия, инженерная и компьютерная графика» Омского государственного технического университета. Основное направление научных исследований — автоматизированная оценка графических построений. Общее количество публикаций - 16.

E-mail: elenashmulenkova@rambler.ru.