1. Построение рядов распределения. Основные показатели ряда

Среднее значение признака (xi ) в каждом интервале дано в графе 3. Результаты умножения вариантов (xi ) на веса ( f i ) показаны в графе 4.

Средняя арифметическая определяет наиболее типичное значение основных средств предприятий в данной совокупности.

x 472 9,44 (млрд. руб.). 50

При анализе деятельности предприятия вычисляется система средних показателей. Например, показатели средней заработной платы оцениваются совместно с показателями средней выработки, фондовооруженности и энерговооруженности труда, степенью механизации и автоматизации работ и др.

Кроме степенных средних в статистических исследованиях используются структурные средние, к которым относятся мода и медиана.

1.3.2.Структурные средние

Это особый класс средних величин. Они используются для изучения внутреннего строения и структуры рядов распределения значений признака. К данному классу относятся показатели моды (Мо) и медианы (Ме). Это дополнительные характеристики совокупности, которые используются в математической статистике для анализа формы рядов распределения [15].

Мода (наиболее часто встречающееся значение признака у единиц совокупности) для дискретного ряда определяется непосредственно как вариант х, имеющий наибольшую частоту или частость. Для интервального ряда с равными интервалами мода рассчитывается по формуле

где xo – начальная (нижняя) граница модального интервала; h- величина интервала; f2 – частота модального интервала; f1 – частота интервала, предшествующего модальному; f3 – частота интервала, следующего за модальным.

Рассчитаем структурные средние для задачи 1.2.

23

Конорева А.А., Харинова М.Ю. Экономико-статистические методы исследования систем при управлении предприятиями дорожной отрасли

Наибольшую частоту (16) имеет интервал 7–9. Тогда мода находится по формуле

Вывод. Наиболее часто в данной совокупности встречаются предприятия, со стоимостью основных средств в размере 8,2 млрд. руб.

Алгоритм для нахождения медианы (значения признака у средней единицы ранжированного ряда):

1.Определяется её порядковый номер (Nме= fi /2).

2.По столбцу накопленных частот определяется сама медиана (для дискретных рядов), или медианный интервал (для интервальных рядов).

3.Значение медианы определяется по формуле

где xo – нижняя граница медианного интервала; fi /2 – порядковый номер медианы; SMe 1 – накопленная частота до медианного интервала; fMe – частота медианного интервала.

Рассчитаем медиану для задачи 1.2.

2. По столбцу накопленных частот определяем, что двадцать пятое предприятие находится в интервале 7–9. Это медианный интервал.

3. Определяем значение медианы

M e 7 2 25 9 9 (млрд. руб.).

16

Вывод. У половины предприятий стоимость основных средств меньше 9 млрд. руб., а у другой половины – больше.

Мода и медиана могут совпадать со значением средней арифметической, в случае симметричного распределения частот вариационного ряда. Соотношение моды, медианы и средней арифметической позволяет оценить асимметрию ряда распределения

[15].

24

1. Построение рядов распределения. Основные показатели ряда

Кроме аналитического способа расчета структурных средних существует графический способ расчет моды и медианы: мода определяется с помощью гистограммы, а медиана – по кумуляте.

Графически изобразим моду и медиану для задачи 1.2.

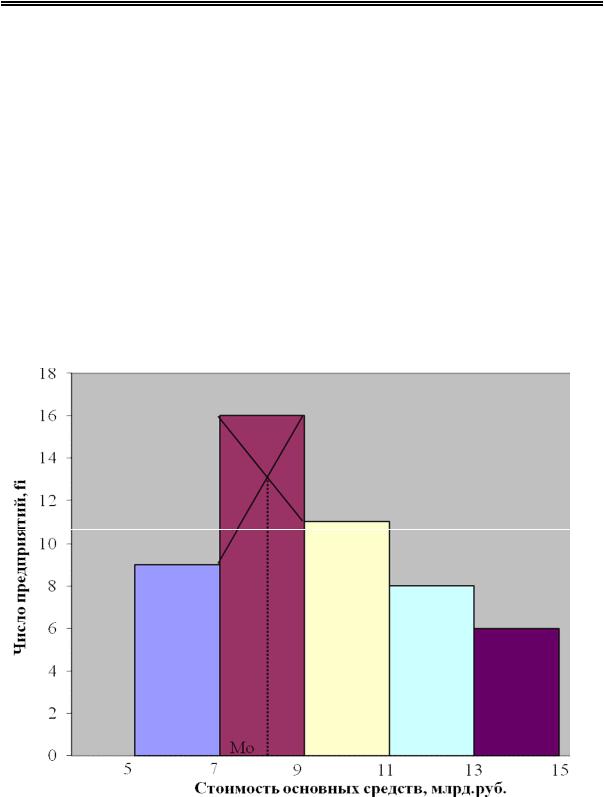
Строится гистограмма распределения 50-ти предприятий по стоимости основных средств (рис. 1.5), для чего на оси абсцисс строится ряд сомкнутых прямоугольников, у каждого из которых основанием служит величина интервала признака (стоимости основных средств), а высотой – частота каждого интервала (число предприятий).

В прямоугольнике, имеющем наибольшую высоту, проводится две линии, как показано на рисунке, и из точки их пересечения опускается перпендикуляр на ось абсцисс. Значение х на оси абсцисс в этой точке и есть мода.

Рис. 1.5. Гистограмма распределения предприятий по стоимости основных средств (графическое нахождение моды)

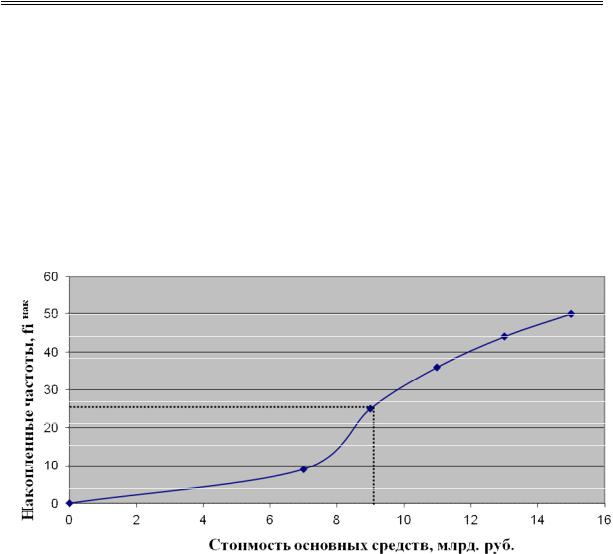
Для графического нахождения медианы по накопленным частотам строится кумулята. Для этого из верхней границы каждого

25

Конорева А.А., Харинова М.Ю. Экономико-статистические методы исследования систем при управлении предприятиями дорожной отрасли

интервала на оси абсцисс восстанавливается перпендикуляр, соответствующий по высоте накопленной частоте с начала ряда по данный интервал. Соединив последовательно вершины перпендикуляров, получается кумулятивная кривая. Из точки на оси ординат, соответствующей половине всех частот (порядковому номеру медианы), проводится прямая, параллельная оси абсцисс, до пересечения ее с кумулятой. Опустив из этой точки перпендикуляр на ось абсцисс, находится значение медианы. Пользуясь кумулятой, можно определить значение признака у любой единицы ранжированного ряда.

Рис. 1.6. Кумулятивная кривая распределения предприятий по стоимости основных средств

1.3.3. Показатели вариации

Вариация – это различия в численных значениях признака. Изучение отклонений от средней величины имеет большое значение в статистических исследованиях, так как в них проявляется развитие изучаемого явления. Для измерения вариации используются показатели колеблемости: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, коэффициент вариации, дисперсия.

Размах вариации R – это величина разности между максимальным и минимальным значениями признака. Недостаток

26

1. Построение рядов распределения. Основные показатели ряда

показателя в том, что он опирается только на крайние значения и не учитывает изменения внутри совокупности:

Среднее линейное отклонение (d) – это средняя арифметическая из абсолютных отклонений индивидуальных значений признака от средней арифметической. Показатель даёт обобщающую характеристику распределению отклонений, учитывает различия всех единиц совокупности. Чем оно меньше, тем однороднее совокупность. В статистической практике применяется редко, т.к. часто не улавливает степень рассеивания.

Среднее квадратическое отклонение (S) – это обобщающая характеристика размеров вариации признака совокупности. Равно квадратному корню из среднего квадрата отклонений индивидуальных значений признака от среднего арифметического. Среднее квадратическое отклонение показывает как расположена основная масса единиц совокупности относительно средней арифметической. В соответствии с теоремой П.Л. Чебышева (1821 – 1894) можно утверждать, что независимо от формы распределения 75% значений признака попадают в интервал x 2S , а по крайней мере 89% всех значений попадают в интервал x 3S [17].

И среднее линейное, и среднее квадратическое отклонения показывают, на сколько единиц в среднем индивидуальные значения признака отклоняются от среднего арифметического значения. Они являются абсолютной мерой колеблемости признака и выражаются в тех же единицах, что и варианты изучаемого признака. Среднее квадратическое отклонение всегда больше среднего линейного отклонения. Если распределение признака ближе к нормальному или симметричному распределению, то между S и d существует взаимосвязь: S=1,25d, или d=0,8S, т.е. если d/S>0,8, то значения признака неустойчивы (в совокупности имеются аномальные значения). Среднее квадратическое отклонение является критерием надёжности средней величины. Чем оно меньше, тем лучше средняя арифметическая отражает изучаемую совокупность. Формулы расчета отклонений для сгруппированных и не сгруппированных данных приведеныв табл. 1.8.

Коэффициент вариации – относительный показатель вариации используется для сравнительной оценки вариации единиц

27

Конорева А.А., Харинова М.Ю. Экономико-статистические методы исследования систем при управлении предприятиями дорожной отрасли

совокупности и для характеристики однородности совокупности. Данный показатель является критерием надежности средней величины. Совокупность считается количественно однородной и средняя арифметическая выбрана надежно, если коэффициент вариации не превышает 40%. Если коэффициент вариации превышает 40%, то это свидетельствует о большей колеблемости единиц совокупности по определенному признаку. Рассчитывается по формуле

S 100%, x

где S – среднее квадратическое отклонение: x – среднее арифметическое.

Коэффициент вариации показывает, насколько % в среднем индивидуальные значения признака отличаются от среднего арифметического значения.

Дисперсия (D) – это средняя из квадратов отклонений значений признака от их средней величины. Формулу для расчета дисперсии можно преобразовать [17]:

Дисперсия равна разности средней из квадратов значений признака и квадрата средней арифметической.

Свойства дисперсии:

1.Дисперсия постоянной величины равна 0.

2.Если все варианты значений признака уменьшить на одно и то же число, то дисперсия не изменится.

3.Если все варианты значений признака уменьшить в одно и то же

число раз (k раз), то дисперсия уменьшится в k2 раз.

Для определения влияния отдельных факторов (причин) на вариацию признака, изучаемая совокупность подразделяется на группы, однородные по признаку – фактору. Правило сложения

1. Построение рядов распределения. Основные показатели ряда

дисперсия признака равна сумме величин межгрупповой дисперсии и средней из внутригрупповых дисперсий. В табл. 1.6 представлены формулы для расчета трех показателей колеблемости признака: общая дисперсия, межгрупповая дисперсия и средняя из внутригрупповых дисперсий.

Показатели вариации рассчитываются для количественных признаков и для альтернативных. Альтернативным называется признак, которым обладают одни единицы совокупности и не обладают другие (два взаимоисключающих варианта). Наличие альтернативного признака обозначается «1», а его отсутствие – «0». Доля вариантов, обладающих признаком, обозначается «p», а доля вариантов, не обладающих – «q»: p+ q=1.

Конорева А.А., Харинова М.Ю. Экономико-статистические методы исследования систем при управлении предприятиями дорожной отрасли

Задача 1.5. Имеются данные о результатах экзаменационной сессии по двум вузам: в первом вузе 80% студентов сдали сессию без двоек, а во втором – 70%. Определить дисперсию доли студентов, успешно сдавших сессию.

Вывод. В первом вузе дисперсия и среднее квадратическое отклонение доли студентов, успешно сдавших сессию, меньше, чем во втором.

Дисперсия представляется в квадратах единиц, в которых измеряется изучаемый признак. Дисперсия и среднее квадратическое отклонение – наиболее широко применяемые показатели вариации,

30

1. Построение рядов распределения. Основные показатели ряда

т.к. они входят в большинство теорем теории вероятности, служащих фундаментом математической статистики. Кроме того, дисперсия может быть разложена на составные элементы, позволяющие оценить влияние различных факторов, обуславливающих вариацию признака.

Рассчитаем показатели вариации для задачи 1.2.

Таблица 1.8

Формулы для расчета абсолютных показателей вариации

31