2334

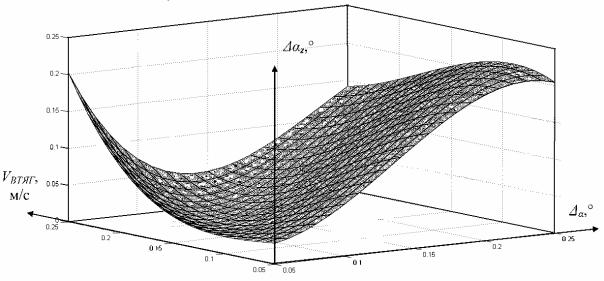
Задача аппроксимации решается также в автоматизированном режиме посредством специального набора команд в командной стро-

ке MATLAB:

а) команда формирования файл-функции: function z = Da(Vv,da)

z = p00 + p10*Vv + p01*da + p20*Vv.^2 + p11*Vv.*da + p02*da.^2 + p30*Vv.^3 + p21*Vv.^2.*da + p12*Vv.*da.^2 + p03*da.^3;

б) команда запуска аппроксимации: ft = fittype( 'poly33' ); opts = fitoptions( ft ); opts.Weights = zeros(1,0);

[fitresult, gof]=fit( [Vv, da], Da, ft, opts).

Полученное уравнения регрессии зависимости αz = f(VВТЯГ; α)

для τгп = 0,1с:

Рис. 4.9. График регрессионной зависимости αz = f(VВТЯГ; α)

При этом R2 = 0,9206. На рис. 4.9 представлен график полученной регрессионной зависимости αz = f(VВТЯГ; α) для значения времени запаздывания гидропривода τгп= 0,1 с.

Полученное уравнения регрессии зависимости tпп = f(VВТЯГ; α)

для τгп = 0,1с:

100

При этом R2 = 0,9993.

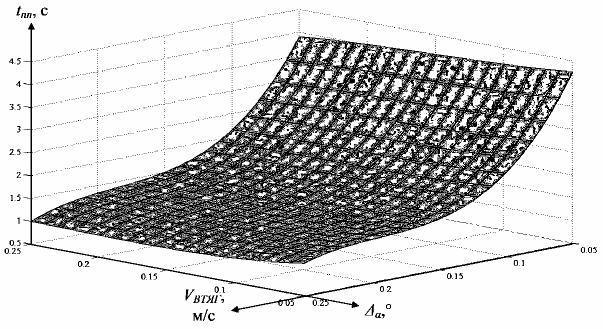
На рис. 4.10 представлен график полученной регрессионной зависимости tпп = f(VВТЯГ; α) для значения времени запаздывания гидропривода τгп = 0,1 с.

Рис. 4.10. График регрессионной зависимости tпп = f(VВТЯГ; α)

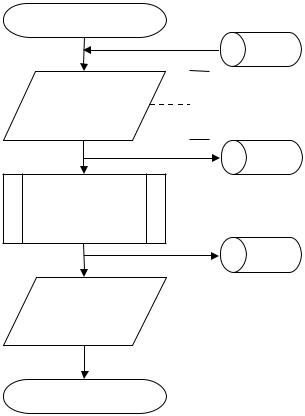
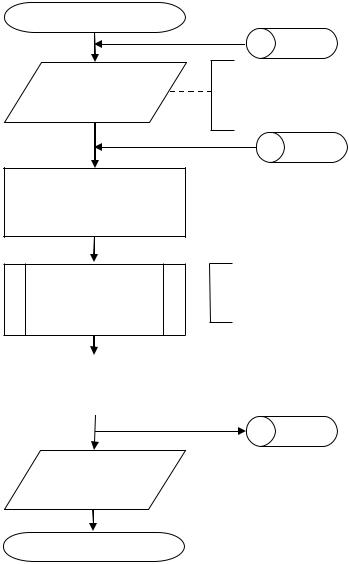
Алгоритм аппроксимации численных зависимостей αz, tпп от

VВТЯГ и α графически представлен в виде блок-схемы на рис. 4.11 и состоит из следующей последовательности действий:

а) чтение массивов входных (VВТЯГ; α) и выходных переменных

αz, tпп;

б) выбор вида уравнения регрессии, запись файл-функции (@ αz, @tпп) с уравнением регрессии в рабочую область MATLAB;

в) расчет коэффициентов уравнений регрессии и коэффициентов детерминации R2, запись их в рабочую область MATLAB;

г) проверка достоверности полученных уравнений по величине

R2.

Полученные уравнения регрессии позволили перейти к поиску оптимальных параметров.

Задачи оптимизации с точки зрения методов решения делятся на два класса [6]:

101

задачи безусловной оптимизации;

задачи условной оптимизации.

Начало αz_nm, tпп_nm, VВТЯГ_n, α_m

Расчет @ αz, @tпп коэффициентов

уравнения

регрессии

p00…pij, R2

Вывод p00…pij, R2

Останов

Рис. 4.11. Блок-схема алгоритма аппроксимации зависимостей αz = f(VВТЯГ; α) и tпп = f(VВТЯГ; α)

Задача безусловной оптимизации представляет собой поиск оптимума целевой функции без всяких дополнительных условий и ограничений [22]:

Задача условной оптимизации в общем виде записывается [22]

i1,...,m; j 1,...,n.

Всистему уравнений (4.11) входят три составляющие:

целевая функция F = f(xj) показывает, в каком смысле решение должно быть оптимальным, то есть наилучшим, при этом возможны

102

три вида назначения целевой функции: максимизация, минимизация, назначение заданного значения;

ограничения gi(xj)≤bi устанавливают зависимости между переменными;

граничные условия dj≤xj≤Dj показывают, в каких пределах могут находиться значения искомых переменных в оптимальном решении.

При решении задач оптимизации в настоящей работе целевая функция и граничные условия были представлены в следующем виде:

Ri ≥ Rmin;

Lmin пред ≤ Li ≤ Lmax пред.

Для решения задачи условной оптимизации было решено воспользоваться методом множителей Лагранжа, который применим при наличии функциональных ограничений вида [22]

где j = 1, 2,…, m.

Для целевой функции Z (x1, x2,…, xn) справедливо уравнение [22]

Продифференцировав равенство (4.13), получим [22]

Каждое из полученных m уравнений теперь умножим на пока еще неизвестный параметр λ, называемый множителем Лагранжа [22]:

103

Сложив уравнения (4.13) и уравнение (4.16), получим [22]

Поскольку все параметры xi независимы, то для того, чтобы это уравнение удовлетворялось, достаточно, чтобы каждый из n членов равнялся нулю, получаем n уравнений [22]:

Таким образом, для перехода к методу множителей Лагранжа необходимо преобразовать ограничения-неравенства в уравнения, после чего целевая функция приобретет вид [22]

i 1,...,m; j 1,...,n.

Таким образом, была поставлена задача условной оптимизации при помощи задания целевой функции и граничных условий и осуществлен переход от нее к безусловной оптимизации.

104

Для решения задачи безусловной оптимизации был использован модифицированный метод Ньютона, основанный на пересчете матрицы Гессе формулой Бройзена-Флетчера-Гольдфарба-Шанно (алгоритм BFGS), реализованный в программном комплексе

MATLAB [22].

Стратегия данного метода состоит в построении последовательности точек {xk}, k = 0,1,…,n, таких, что f(xk+1) < f(xk). Точки последовательности вычисляются по правилу [22]

где х0 задается пользователем, а направление спуска βk∙sk определяется для каждого значения k по формулам [22]:

где H – матрица Гессе; f (xk ) – градиент функции f(x) в точке xk. Формула пересчета Бройзена-Флетчера-Гольдфарба-Шанно

(BFGS) [22]:

Построение последовательности {xk} заканчивается в точке xk при условии

где ε – заданное малое положительное число (точность приближения). Программный комплекс MATLAB позволяет проводить оптими-

зацию функциональных зависимостей вида z = f(x,y) вышеописанным методом при помощи встроенного пакета «Optimization Tool» (рис. 4.12), представляющего собой оконный интерфейс с возможностью

105

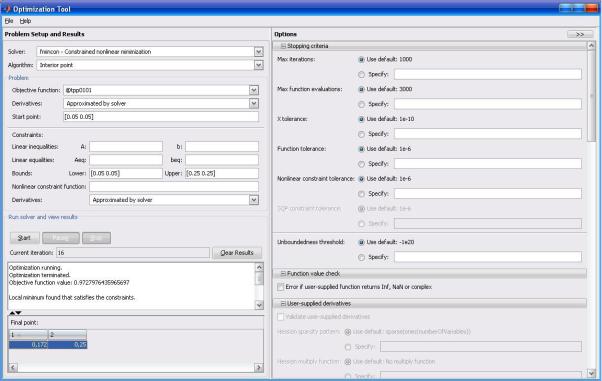
задания настроек оптимизации, оптимизируемой функции и граничных условий [4].

Задача оптимизации может решаться также в автоматизированном режиме посредством специального набора команд в командной строке MATLAB:

function [x,fval,exitflag,output,lambda,grad,hessian] = Opttpp(x0,lb,ub)

options=optimset;

options=optimset(options,'Display','off'); options=optimset(options,'Algorithm','interiorpoint'); fmincon(@tpp,x0,[],[],[],[],lb,ub,[],options);

Таким образом были получены оптимальные значения основных параметров устройства управления положением платформы строительной машины: VВТЯГ= 0,25 м/с; α = 0,172 .

Рис. 4.12. Внешний вид окна инструмента «Optimization Tool»

Алгоритм оптимизации параметров VВТЯГ и α по целевой функции критерия эффективности tпп графически представлен в виде блоксхемы на рис. 4.14 и состоит из следующей последовательности действий:

106

а)постановка задачи оптимизации: файл-функция (@tпп) с коэффициентами (p00…pij), ее оптимум, точка начала оптимизации (x0) и граничные условия (lb,ub);

б)нахождение интервала значений VВЫД, α для заданной точно-

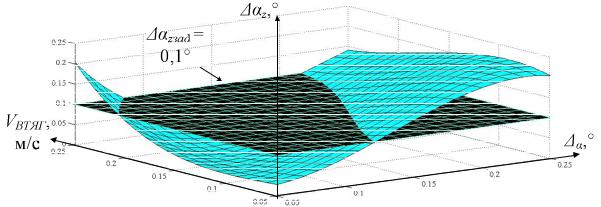
сти αz (рис. 4.13);

в) переход от задачи условной к задаче безусловной оптимизации, используя метод множителей Лагранжа;

г)нахождение оптимума целевой функции и соответствующих ему переменных VВТЯГ и α;

д)запись найденных оптимальных значений αz, tпп, VВТЯГ, α в рабочую область MATLAB.

Рис. 4.13. График регрессионной зависимости αz = f(VВТЯГ; α) с наложенными ограничениями αzзад

Проведенный анализ, аппроксимация и оптимизация основных параметров устройства управления положением платформы строительной машины позволили составить алгоритм оптимизационного синтеза, графически представленный в виде блок-схемы на рис. 4.15.

Оптимизационный синтез состоит из следующей последовательности действий:

1.Постановка задачи оптимизации: выбор целевой функции: tпп=f(VВТЯГ; α) → min.

2.Аппроксимация численных зависимостей tпп и αz от VВТЯГ и α согласно алгоритму оптимизации (рис. 4.14): получение коэффициентов уравнения регрессии – полинома 3-й степени.

3.Решение задачи условной оптимизации параметров, используя методы множителей Лагранжа и Ньютона: расчет и запись в рабочую

область MATLAB оптимальных значений параметров αz, tпп, VВТЯГ и

107

α как результата решения задачи условной оптимизации целевой функции tпп = f(VВТЯГ; α) → min.

Рис. 4.14. Блок-схема алгоритма оптимизации основных параметров устройства управления положением платформы строительной машины

Результатом оптимизационного синтеза являются оптимальные значения скорости выдвижения аутригеров платформы строительной машины VВТЯГ и значение зоны нечувствительности порогового элемента α при определенном времени запаздывания гидропривода τгп.

108

5. СИСТЕМА АВТОМАТИЗАЦИИ ПРОЕКТИРОВАНИЯ ОСНОВНЫХ ПАРАМЕТРОВ УСТРОЙСТВА УПРАВЛЕНИЯ ПОЛОЖЕНИЕМ ПЛАТФОРМЫ СТРОИТЕЛЬНОЙ МАШИНЫ

В настоящей работе автоматизация проектирования устройства управления платформой строительной машины была сведена к автоматизации расчета оптимальных параметров: скорости перемещения аутригеров платформы VВЫД и ширины зоны нечувствительности порогового элемента α. На основе проведенных в работе теоретических исследований процесса управления положением платформы строительной машины была разработана инженерная методика оптимизации основных параметров устройства управления положением платформы строительной машины.

Инженерная методика заключается в следующем:

1.Для имеющейся математической модели процесса управления положением платформы строительной машины определить значения постоянных параметров:

а)по конструкторской документации на строительную машину определить параметры платформы: a, b;

б)по технической документации определить параметры гидропривода системы управления аутригерами платформы: dц, dш, c1,с2, с3,

mзол, гп;

в)исходя из требований, предъявляемых к строительной машине,

задать αzзад.

2.Определить диапазоны и шаги изменения оптимизируемых параметров устройства управления положением платформы строительной машины:

а) диапазон (VВТЯГ min, VВТЯГ max) и шаг ∆VВТЯГ изменения скорости выдвижения аутригеров платформы;

б) диапазон ( α min, α max) и шаг ∆ α изменения ширины зоны нечувствительности порогового элемента.

3.Провести исследования на ПЭВМ: решение математической модели процесса управления положением платформы строительной машины и получение массивов значений αz, tпп от оптимизируемых

параметров VВТЯГ и α.

4.Выполнить аппроксимацию полученных численных зависимостей αz, tпп от VВТЯГ и α методом наименьших квадратов.

5.Найти интервалы допустимых значений VВТЯГ и α для заданной точности αzзад.

109