Задание на курсовую работу

Задание 1.

1.1 Вывести передаточные функции разомкнутой и замкнутой систем автоматического управления, относительно входного воздействия.

1.2 Вывести дифференциальные уравнения САУ, разомкнутой и замкнутой.

1.3 Вывести формулой для вещественной и мнимой компонент АФЧХ САУ, замкнутой и разомкнутой САУ.

Задание 2.

2.1 Составить таблицу расчетных значений построения графиков частотных характеристик.

2.2 Построить графики АФЧХ замкнутой и разомкнутой САУ.

2.3 Построить графики логарифмической амплитудной и фазовой характеристики разомкнутой и замкнутой САУ.

Задание 3.

3.1 Построить асимптотическую ЛАЧХ разомкнутой САУ.

3.2 Построить желаемую асимптотическую ЛАЧХ разомкнутой корректированной САУ, которая удовлетворяет требованию задания по перерегулированию и времени переходного процесса.

3.3 Построить асимптотическую ЛАЧХ последовательного корректированного устройства.

Исходные данные:

	K1	K2	K3	T1	T2	T3	tрег		Lм
Вар.2.4.	6	3	2	0,5(с)	0,4(с)	0,1(с)	2,6(с)	40%		33

Задание 1

1.1 Вывод передаточной функции разомкнутой и замкнутой сау, относительно входного воздействия

В общем случае, передаточная функция разомкнутой системы из последовательных звеньев можно представить в виде:

.

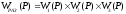Подставляя значения передаточных функций, получим выражение вида:

.

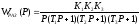Для замкнутой системы с отрицательной обратной связью, передаточная функция по отношению к входному воздействию имеет вид:

.

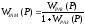Подставляя значения передаточных функций, получим выражение вида:

.

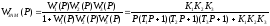1.2 Вывод дифференциальных уравнений сау

В общем виде дифференциальное уравнение для разомкнутой системы имеет вид:

.

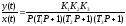Запишем выражение для

.

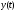
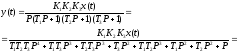
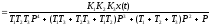Для перехода к дифференциальной форме произведем замену 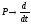и получим уравнение вида:

.

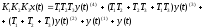В общем виде дифференциальное уравнение для замкнутой системы имеет вид:

.

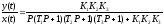Запишем выражение для

.

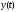
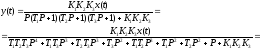
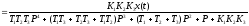Для перехода к дифференциальной форме произведем замену 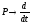и получим уравнение вида:

.

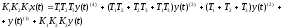1.3 Вывод формул для мнимой и вещественной компонент афчх сау, замкнутой и разомкнутой сау

Для перехода в частотную область произведем замену

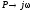
Тогда частотная передаточная функция для разомкнутой системы примет вид:

.

Введем обозначения:

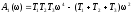, (1)

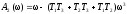. (2)

Получим выражение вида:

.

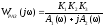
Для перехода к комплексной форме домножим числитель и знаменатель на сопряженный множитель и получим:

.

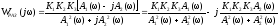Обозначим за:

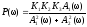, (3)

где 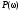- вещественная компонента.

Обозначим за:

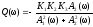, (4)

где 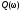- мнимая компонента.

Получим частотную передаточную функцию вида:

.

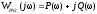Частотная передаточная функция для замкнутой системы имеет вид:

.

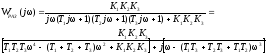Введем обозначения:

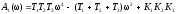, (5)

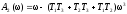. (6)

Получим выражение вида:

.

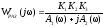
Для перехода к комплексной форме домножим числитель и знаменатель на сопряженный множитель и получим:

.

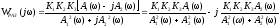Обозначим за:

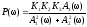, (7)

где 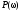- вещественная компонента.

Обозначим за:

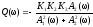, (8)

где 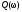- мнимая компонента.

Получим частотную передаточную функцию вида:

.
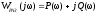