
2209
.pdf
|
Глава 5. РАЗРАБОТКА ПЛАНА |
|
ПЕРЕВОЗОК ГРУЗОВ |
|
|
|
Аэi |
18. |
Суммарная выработка в тоннах Qн = Qi = 40 т. |
|
1 |
19. |
Суммарная выработка в тонно-километрах |
|
Аэi |
|
Рн = Рi = 450+450+300 = 1200 т∙км. |
|
1 |
|
Аэi |
20. |
Суммарный общий пробег Lобщ= Lобщi = 190+190+130 = 510 км. |
|
1 |
21. |
Суммарное отработанное время |
Аэi
Тн факт= Тнфакт i = 9,1+9,1+6,2 = 24,4 ч.
1
Результаты расчета занесем в табл. 20
Контрольные вопросы
1.Как выполняется нахождение маятниковых маршрутов, с обратным негруженым пробегом?
2.Как на маятниковом маршруте, с обратным негруженым пробегом, определить плановый объем перевозок?
3.Для чего выполняется проверка равенства объема перевозок и сменной выработки одного автомобиля?
4.Для чего рассчитывается пропускная способность грузового пункта?
5.Как рассчитывается пропускная способность грузового пункта?
6.Как рассчитать число оборотов на маятниковых маршрутах, с обратным негруженым пробегом?
7.Что является основанием для перехода к нахождению маятниковых маршрутов, с обратным негруженым пробегом?
8.Назовите причину разной выработки автомобилей.
9.Назовите причину вычитания одного холостого пробега при расчете общего пробега каждого автомобиля за время в наряде на маятниковом маршруте, с обратным негруженым пробегом.
10.Как рассчитываются результаты работы группы автомобилей на маятниковом маршруте, с обратным негруженым пробегом?
Продолжаем нахождение возможных маятниковых маршрутов, с обратным негруженым пробегом.
Осталась заявка по табл. 19, это В2А4=10 т, поэтому рассмотрим маятниковый маршрут В2А4А4В2, с обратным негруженым пробегом.
5.1. Составление схемы маршрута и нулевых пробегов.
Схема маятникового маршрута В2А4А4В2, с обратным негруженым пробегом и нулевых пробегов, представлена на рис. 50. По рис. 4 находим пробеги: lг = 30 км; lх = 30 км; lн1 = 30 км; lн2 = 30 км.
~ 181 ~
Витвицкий Е.Е. ТЕОРИЯ ТРАНСПОРТНЫХ ПРОЦЕССОВ И СИСТЕМ (ГРУЗОВЫЕ АВТОМОБИЛЬНЫЕ ПЕРЕВОЗКИ)
lг
В2 |
|
|
А4 |
Рис. 50. Схема маятникового маршрута, |
|
|
|||
|
|
|
|
с обратным негруженым пробегом |
|
lх |
|
|
В2А4А4В2 и нулевых пробегов |
|
lн1 |
lн2 |
|
|
 АТП
АТП
5.2. Расчет работы одного автомобиля.
1.Длина маршрута lм = lг+ lх = 30+30 = 60 км.
2.Время ездки (оборота) tе,o= (lм/Vт) +tпв = 60/25+0,5 = 2,9 ч.
3.Выработка в тоннах за ездку (оборот) Qе,о = q·γ = 5 т.
4.Выработка в тонно-километрах за ездку (оборот) Ре,о = q·γ·lг = =5∙30=150 т∙км.
5.Число ездок автомобиля за время в наряде Ze=[Tн/ tе]=8/2,9=2,75=?
где 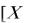
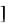 – целая часть числа Х.
– целая часть числа Х.
6. Проверка возможности исполнения ездки на последнем обороте. Остаток времени в наряде, после исполнения целых ездок, составит
∆Тн = Тн [Tн / tе]· tе = 8 – 5,8 = 2,2 ч, время ездки необходимое (погрузка + + перевозка груза + разгрузка) tен = (lг/Vт) + tпв = 1,2+0,5=1,7 ч, 1,7 2,2, поэтому автомобиль может выполнить за время в наряде 3 ездки.
Zе
7. Выработка в тоннах автомобиля за время в наряде Qн = q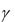 = 15 т.
= 15 т.
1
5.3. Проверка равенства объема перевозок и сменной выработки одного автомобиля.
8.Сравнивая Qплан и Qн одного автомобиля, получаем, что один автомобиль может выполнить Qплан, следовательно, дальнейшие расчеты проводим для случая применения одного автомобиля на маршруте.
9.Выработка в тоннах автомобиля за время в наряде
Zеi
Qн = q i ; Qн1 = 10 т.
1
15. Выработка в тонно-километрах автомобиля за время в наряде
Zеi
Рнi = q γi lг . Рн = 300 т∙км.
1
16. Общий пробег автомобиля за время в наряде
~ 182 ~

Глава 5. РАЗРАБОТКА ПЛАНА ПЕРЕВОЗОК ГРУЗОВ
Lобщi = lн1+ +lм∙Zei + lн2 – lх. Lобщ = 150 км. 17. Время в наряде автомобиля фактическое
Zе
Тн фактi = (Lобщi / Vт) +
1
i
tпв . Тн факт = 150/25 + 2∙0,5 = 7,0 ч.
Результаты расчета занесем в табл. 20.
|
|
|
|
|
Таблица 20 |
План перевозок грузов автомобилями грузоподъемностью 5 т |
|
||||
|
|
|
|
|
|
Маршрут |
Qпл, т |
Рд, т∙км |
Lобщ, км |
ΣТнфакт, ч |
Апл, ед. |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
Е4F3F3Е4 |
40 |
800 |
420 |
20,8 |
2,0 |
В т.ч.: 1 авто |
20 |
400 |
210 |
10,4 |
|
2 авто |
20 |
400 |
210 |
10,4 |
|
F3E4E4F3 |
80 |
1600 |
540 |
29,6 |
3,0 |
В т.ч.: 1 авто 1 группа |
30 |
600 |
200 |
11,0 |
|
2 авто 1 группа |
30 |
600 |
180 |
10,2 |
|
1 авто 2 группа |
20 |
400 |
160 |
8,4 |
|
А6В2В2А4А4А6 |
40 |
1600 |
580 |
27,2 |
3,0 |
В т.ч.: 1 авто 1 группа |
15 |
650 |
230 |
10,7 |
|
2 авто 1 группа |
15 |
550 |
200 |
9,5 |
|
1 авто 2 группа |
10 |
400 |
150 |
7,0 |
|
D5D3Е4А3D5 |
120 |
4800 |
1980 |
91,2 |
12,0 |
В т.ч.: 1 авто 1 группа |
10 |
400 |
150 |
7,0 |
|
2 авто 1 группа |
10 |
400 |
180 |
8,2 |
|
1 авто 2 группа |
10 |
400 |
150 |
7,0 |
|
2 авто 2 группа |
10 |
400 |
180 |
8,2 |
|
1 авто 3 группа |
10 |
400 |
150 |
7,0 |
|
2 авто 3 группа |
10 |
400 |
180 |
8,2 |
|
1 авто 4 группа |
10 |
400 |
150 |
7,0 |
|
2 авто 4 группа |
10 |
400 |
180 |
8,2 |
|
1 авто 5 группа |
10 |
400 |
150 |
7,0 |
|
2 авто 5 группа |
10 |
400 |
180 |
8,2 |
|
1 авто 6 группа |
10 |
400 |
150 |
7,0 |
|
2 авто 6 группа |
10 |
400 |
180 |
8,2 |
|
С3D5D5D3С3 |
20 |
600 |
180 |
9,2 |
1,0 |
В т.ч.: 1 авто |
20 |
600 |
180 |
9,2 |
|
C3D5D5C3 |
40 |
1200 |
510 |
24,4 |
3,0 |
В т.ч.: 1 авто 1 группы |
15 |
450 |
190 |
9,1 |
|
2 авто 1 группы |
15 |
450 |
190 |
9,1 |
|
3 авто 1 группы |
10 |
300 |
130 |
6,2 |
|
B2А4А4B2 |
10 |
300 |
150 |
7,0 |
1,0 |
В т.ч.: 1 авто |
10 |
300 |
150 |
7,0 |
|
Итого |
350 |
10900 |
4360 |
209,4 |
25,0 |
|
|
|
|
|
|
~ 183 ~



Витвицкий Е.Е. ТЕОРИЯ ТРАНСПОРТНЫХ ПРОЦЕССОВ И СИСТЕМ (ГРУЗОВЫЕ АВТОМОБИЛЬНЫЕ ПЕРЕВОЗКИ)
где w! факториал целого положительного числа w, который равен произведению: w! = 1 2 3 ... w. При трех пунктах завоза груза количество возможных маршрутов М = w! = 3! = 1 2 3 = 6, таким образом, возможны шесть маршрутов доставки груза из пункта А (табл. 21). Выбор маршрута осуществляется по критерию «минимум затрат», чему соответствует минимум пробега. При наличии двух и более маршрутов одинаковой протяженности цели системы соответствует минимум грузооборота на маршруте. Результаты расчета пробега, формула (4.41), и выработки в т∙км, формула (4.45), представлены в табл. 21.
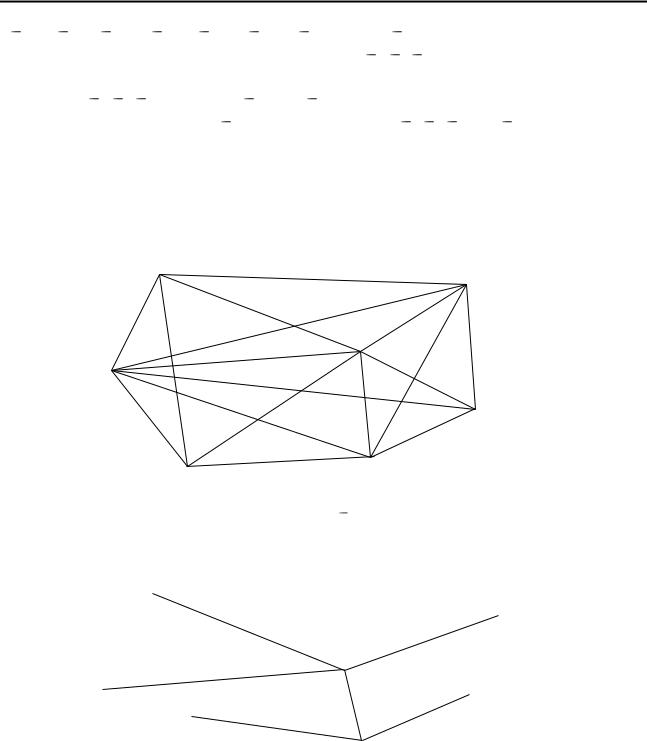
Принимаем для дальнейшего проектирования маршрут № 1 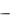 А В1 В2 В3 А, поскольку ему соответствует минимальный пробег и выработка в тонно-километрах. Результаты работы автомобиля рассчитываются по формулам (4.41) – (4.45) и представлены в табл. 22.
А В1 В2 В3 А, поскольку ему соответствует минимальный пробег и выработка в тонно-километрах. Результаты работы автомобиля рассчитываются по формулам (4.41) – (4.45) и представлены в табл. 22.
Таблица 21
Результаты расчета пробега и грузооборота на развозочном маршруте
Номер маршрута |
Маршрут |
Пробег, км |
Выработка, т км |
1 |
А-В1-В2-В3-А |
29,0 |
46,0 |
2 |
А-В3-В2-В1-А |
29,0 |
70,0 |
3 |
А-В1-В3-В2-А |
33,0 |
56,0 |
4 |
А-В2-В3-В1-А |
33,0 |
76,0 |
5 |
А-В2-В1-В3-А |
34,0 |
61,0 |
6 |
А-В3-В1-В2-А |
34,0 |
75,0 |
|
|
|
|
Таблица 22 |
Результаты функционирования автомобиля |
||||
|
|
|
|
|
Маршрут |
Q, т |
Lс, км |
tрм , ч |
Р, т км |
А-В1-В2-В3-А |
4,0 |
29,0 |
1,76 |
46,0 |
В случае если перевозимый груз относится к грузам первого класса, для перевозки груза на спроектированном маршруте достаточно автомобиля с грузоподъемностью 4 т. Если нет автомобиля требуемой грузоподъемности или груз не первого класса, то требуется другой автомобиль большей грузоподъемности.
Рассмотренный пример с числом пунктов завоза w = 3. Что будет, если потребителей 4, или 5, или 10? Согласно формуле (5.2) число вариантов маршрутов, которые необходимо будет рассмотреть, обсчитать и т.д., будет равно соответственно 24; 120; 3628800. Решение задачи с числом пунктов завоза более четырех рассмотренным способом в оперативном режиме нерационально.
Контрольные вопросы
1.Назовите условия необходимости решения задачи проектирования развозочных (сборных) маршрутов.
2.Назовите цель решения задачи проектирования развозочных (сборных) маршрутов.
~186 ~
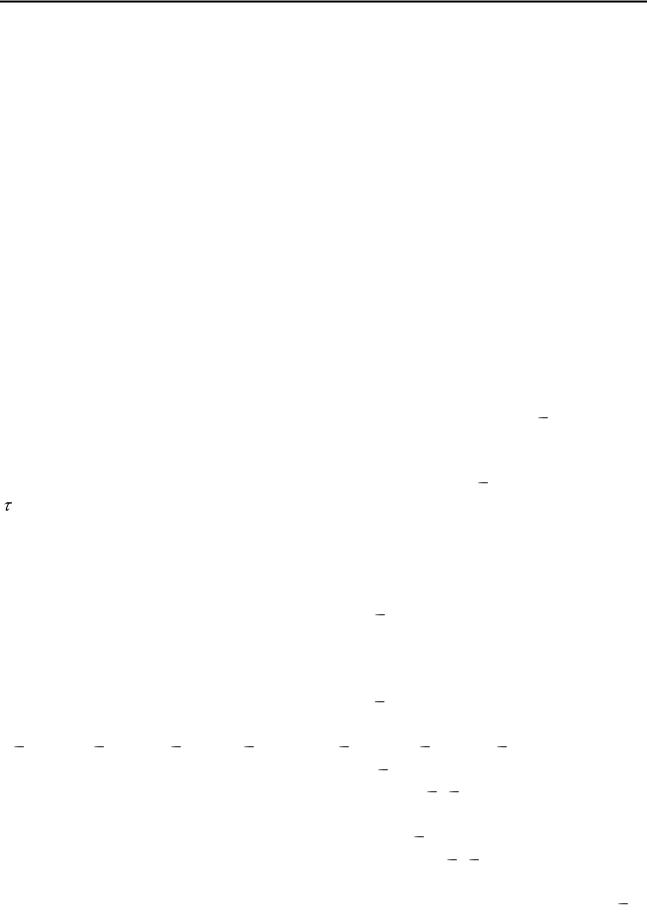



 6
6