
- •Оглавление
- •Основные понятия
- •Принципы управления
- •Алгоритм решения дифференциального уравнения с использованием преобразования Лапласа
- •Пример решения 1
- •Пример решения 2
- •Переходной процесс и его оценки.
- •Импульсная переходная функция
- •Дельта-функция и ее свойства
- •Алгоритмы конструирования множества уу
- •Возможные структуры управляющего устройства
- •Критерии оценки качества системы и управляющего устройства
- •Алгебраические критерии устойчивости Критерий Гурвица
- •Критерий Льенара–Шипара
- •Критерий Михайлова
- •Критерий Найквиста
- •Частотные критерии качества
- •Интегральная квадратичная оценка качества
- •Желаемые и действительные передаточные функции
- •Фильтр Баттерворта (желаемая передаточная функция)
- •Критерии близости действительных передаточных функций к желаемым
- •Интегральная полулогарифмическая функция чувствительности
- •Математические модели ограничений на реализуемость
- •Ограничения, которым должна удовлетворять математическая модель реального объекта
- •Ограничения, которым должна удовлетворять математическая модель уу
- •Соотношения, обеспечивающие реализуемость уу
- •Решение оптимизационной задачи
- •Алгоритм решения уравнения Винера-Хопфа
- •Минимальное значение функционала
Частотные критерии качества
Частотными критериями качества являются запасы устойчивости:
По фазе
По амплитуде
<рисунок>
Интегральная квадратичная оценка качества
Рассмотрим вопрос о том, какие две системы можно считать имеющими близкие характеристики. Для этого запишем соотношения, связывающие выход каждой из этих систем с ее входом:


Системы с
импульсными переходными функциями
 и
и эквивалентны, если
эквивалентны, если при любых
при любых .
Системы с импульсными переходными
функциями
.
Системы с импульсными переходными
функциями и
и можно считать близкими по характеристикам,
если при любых
можно считать близкими по характеристикам,
если при любых выполняется соотношение:
выполняется соотношение:

Такое
соотношение имеет место, если (так как
 произвольное и одинаковое):
произвольное и одинаковое):

Используя равенство Парсеваля получим критерий близости двух динамических систем. Две динамические системы близки, если близки их импульсные переходные функции или частотные передаточные функции:

Желаемые и действительные передаточные функции


Условия,
накладываемые на
 :
:
Должна фильтровать полезный сигнал Mот помехиN.
Должна быть ближе к
 .
.
Система
управления должна воспроизводить не
само воздействие, а некоторые его
составляющие. Например, не само задающее
воздействие, а некоторые функции,
связанные с регулярной
 и случайной
и случайной составляющими:
составляющими:

Желаемые операторы составляющих помех обычно выбираются нулевыми:

Фильтр Баттерворта (желаемая передаточная функция)

Спектр задающего воздействия лежит в области низких частот, тогда как спектр наложенной на него помехи в области высоких частот. Следовательно, хорошая система по своим свойствам близка к идеальному низкочастотному фильтру.
На интервале
 фаза
фаза должна быть равна нулю, после
должна быть равна нулю, после – любой.
– любой.
Квадрат модуля передаточной функции фильтра Баттерворта определяется соотношением:

При
 амплитудная характеристика этого
фильтра стремиться к идеальной
амплитудной характеристике низкочастотного
фильтра:
амплитудная характеристика этого
фильтра стремиться к идеальной
амплитудной характеристике низкочастотного
фильтра:

При
 допустимо соотношение:
допустимо соотношение:

Формула,
определяющая функцию
 ,
имеет вид:
,
имеет вид:
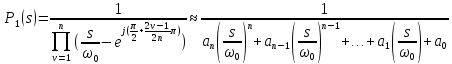
|
|
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
Критерии близости действительных передаточных функций к желаемым
Под действием передаточной функции понимается функционал с произвольно-заданными оптимальными значениями коэффициентов.
Функционал ставит в соответствие каждой функции из некоторого класса число. Величина числа характеризуется близостью сравниваемых передаточных функций. Если они совпадают, функционал равен нулю.
Входящие в функционал действительные и желаемые передаточные функции находятся в классе устойчивых передаточных функций.
Оценки близости желаемых и действительных передаточных функций имеют вид:



Порядок
решения оптимизационной задачи: из
минимумов функционалов
 ,
, ,
, определяются
определяются и
и .
.


Интегральная полулогарифмическая функция чувствительности

Интегральная полулогарифмическая функция чувствительности характеризует изменение передаточной функции всей системы, в зависимости от относительного изменения передаточной функции ее составной части.
Такое определение подтверждается соотношением:


Где:
 – изменение передаточной функции всей
системы.
– изменение передаточной функции всей
системы.
 – относительное изменение передаточной
функции составной части системы.
– относительное изменение передаточной
функции составной части системы.
Алгоритм определения функций чувствительности

Рассмотрим функции чувствительности системы к изменению динамических характеристик наименее стабильного звена в структуре объекта управления:


Функции чувствительности системы относительно изменения входящих в нее звеньев коррекции зависят от структуры управляющего устройства.
Формулы для численной оценки интегральных функций чувствительности
Способ 1
Оценка интегральной функции чувствительности, где под знаком модуля стоят дробно-рациональные функции, через коэффициенты определяется так:

Чтобы найти
коэффициенты
 необходимо представить выражение
необходимо представить выражение в виде произведения:
в виде произведения: ,
раскрыть скобки и вычислить необходимые
коэффициенты.
,
раскрыть скобки и вычислить необходимые
коэффициенты.
 – определитель Гурвица.
– определитель Гурвица.
 – определитель, полученный из определителя
Гурвица путем замены элементов первого
столбца коэффициентами
– определитель, полученный из определителя
Гурвица путем замены элементов первого
столбца коэффициентами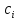 .
.

Способ 2
Другое
соотношение для отыскания
 через вычеты функции имеет вид:
через вычеты функции имеет вид:

Где:
 – полюсы функции
– полюсы функции ,
,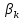 – полюсы функции
– полюсы функции ,
, – вычет функции
– вычет функции в точках
в точках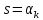 и
и .
Величина вычета может быть вычислена
по формуле:
.
Величина вычета может быть вычислена
по формуле:


Свойство оценки интегральной функции чувствительности
Запишем определитель Гурвица в виде:

Если
 ,
то согласно формуле выше интеграл
расходиться, так как
,
то согласно формуле выше интеграл
расходиться, так как и полином знаменателя имеет в
и полином знаменателя имеет в один нулевой корень.
один нулевой корень.

Где
 – корни характеристического полинома.
Интеграл
– корни характеристического полинома.
Интеграл расходиться, если хотя бы один полюс
расходиться, если хотя бы один полюс находиться на мнимой оси.
находиться на мнимой оси.
Расшифровка
формулы для
 :
:

Оценка сложности УУ на элементах дискретной техники
<пропущено описание дискретной техники>
В теории алгоритмов сложность – понятие, характеризующее количество средств, необходимых для реализации вычислительных функций.
Сложность бывает:
Алгоритмическая – величина, характеризующая размер записи алгоритма на каком-либо алгоритмическом языке.
Вычислительная – оценивается временем работы алгоритма и объемом используемой памяти.
Математические модели ограничений
Требования к математической модели ограничений:
Должна достаточно точно отражать сущность ограничения.
Быть достаточно простой, не усложнять существенно алгоритм решения задачи.
Совокупность ограничений и критериев не должна быть взаимоисключающей.
Форма описания ограничения должна быть такой, чтобы решаемая задача при ограничениях сводилась к классической вариационной задаче.
Замечание по поводу четвертого требования - обычно при оптимизации функционала

Ограничения задаются в виде дополнительных алгебраических уравнений:

Дополнительные условия могут быть представлены в двух видах:




Ограничения накладываются на те же функции, что входят в функционал. Если это не так, ограничениям необходимо придать соответствующую форму.






