Критерий Льенара–Шипара

Условие критерия Гурвица избыточно. Число неравенств можно уменьшить в два раза, используя теорему Льенара-Шипара.

Если все коэффициенты характеристического полинома положительные, то необходимое и достаточное условие устойчивости сводится к положительным определителям Гурвица с чётными или нечётными индексами.

Частотные критерии устойчивости

Пусть объект задан W(s) и он устойчив. На него подаём синусоиду с амплитудойN:

Если на вход подается синусоидальное воздействие, то в установившемся режиме мы получим синусоиду той же частоты, с другой амплитуды и со сдвигом по фазе.

– частотная передаточная функция (комплексная).

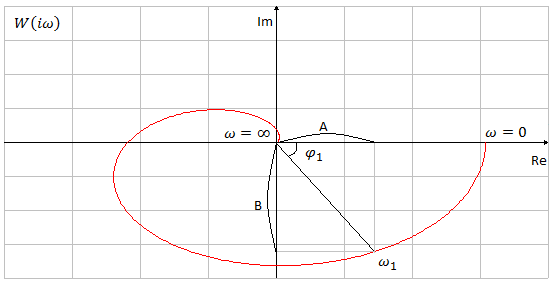
Амплитудно-фазовая характеристика

Амплитудно-фазовая характеристика (АФХ) строится на комплексной плоскости и представляет собой геометрическое место точек концов векторов (годограф) частотной передаточной функции при изменении.

Всякую непрерывную функцию , удовлетворяющую на промежуткеусловиям Дирихле можно разложить на этом промежутке в сходящийся ряд вида:

Свойства частотной характеристики

Любые физические системы характеризуются полосой пропускания.

Полосой пропускания называется диапазон частот (гармонических колебаний), в которых выход заметно изменяется. Обычно считают возможным пренебречь выходными колебаниями, амплитуда которых меньше 5% входных колебаний.

Частота, для которой АФК имеет максимум, называется резонансной частотой, т.к. при этой частоте гармонические колебания получают наибольшее усиление.

Принцип аргумента

Рассмотрим числитель:

Если нуль левый, то при изменении он повернется на(против часовой стрелки). Если таких корней, то угол поворота составит.

Если нуль правый, то при изменении он повернется на(по часовой стрелке). Если таких корней, то угол поворота составит.

Суммарный угол поворота по часовой стрелке

Рассмотрим знаменатель:

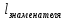Если полюс левый, то при изменении он повернется на(по часовой стрелке). Если таких корней, то угол поворота составит.

Если полюс правый, то при изменении он повернется на(против часовой стрелки). Если таких корней, то угол поворота составит.

Суммарный угол поворота по часовой стрелке

Суммарный угол поворота по часовой стрелке:

Критерий Михайлова

Если все корни характеристического полинома лежат в левой полуплоскости, то система устойчива.

Для того, чтобы все корни характеристического полинома находились в левой полуплоскости, необходимо и достаточно, чтобы годограф Михайлова повернулся нигде не обращаясь в ноль вокруг точкипротив часовой стрелки на, где– количество корней.

Годограф Михайлова начинается на вещественной полуоси, всегда имеет плавную спиралевидную форму, причем конец ее уходит в бесконечность в том квадранте комплексной плоскости, номер которого совпадает со степенью характеристического полинома.

Критерий Найквиста

Позволяет судить об устойчивости замкнутой системы по АФХ разомкнутой системы.

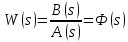
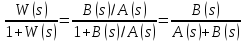
Порядок больше порядка. Составим функцию

Если разомкнутая система неустойчива, т.е. , тогда для того чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы АФК разомкнутой системыпри измененииповернулось против часовой стрелки вокруг точкина угол.

Если разомкнутая система устойчива, т.е. , то замкнутая система будет также устойчива, если АФК разомкнутой системыне охватывает точку.