Алгоритмы конструирования множества уу

Звенья коррекции– функциональные элементы, описываемые дифференциальным уравнением. Имею один вход и один выход. Передаточные функции звеньев коррекции будем обозначать как.

Пусть УУ построено и использованием одного звена коррекции с передаточной функцией 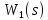, тогда:

Или

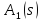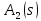При таком конструировании УУ передаточные функции ифункционально связанны, т.е. одного звена коррекции недостаточно для реализации УУ с наперед заданными передаточными функциямии.

Увеличим число звеньев до двух:

При таком конструировании УУ передаточные функци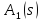и ифункционально независимы, т.е. можно решить систему из двух уравнений с двумя неизвестными и найти точные передаточные функции звеньев коррекци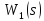ии.

Если в УУ существуют звенья коррекции, передаточные функции которых определяются из дополнительных условий, то такие звенья коррекции называются дополнительнымии обозначаются.

Таким образом, все множество возможных УУ состоит из трех множеств:

1. С достаточным числом звеньев коррекции - если число определяемых звеньев совпадает с числом каналов.

2. С недостаточным числом звеньев коррекции - если число определяемых звеньев меньше числа каналов.

3. С дополнительным числом звеньев – если присутствуют дополнительные звенья коррекции. Это множество может включать в себя УУ как с достаточным, так и с недостаточным числом звеньев коррекции.

Возможные структуры управляющего устройства

С недостаточным числом звеньев коррекции:

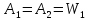
С достаточным числом звеньев коррекции:

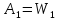
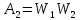
С недостаточным числом звеньев коррекции, а также с дополнительным звеном коррекции:

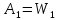
С достаточным числом звеньев коррекции, а также с дополнительным звеном коррекции:

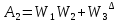
Критерии оценки качества системы и управляющего устройства

Критерий оценки качества – совокупность принимаемых показателей, позволяющих оценить качество системы.

Критерий оценки качества должен удовлетворять ряду требований:

1. Иметь физический смысл, быть адекватным, сформулированным в ТЗ.

2. Быть простым – чем больше требований заложено, тем сложнее на элементной базе реализовать полученное оптимальное решение.

3. Входящие в критерий составляющие не должны быть взаимоисключающими.

4. Форма критерия должна быть такой, чтобы задачу можно было решить аналитически. Это требование оказывается весьма строгим и является главной причиной, обуславливающей широкой применение на практике лишь незначительного числа критериев.

Различают критерии двух видов:

1. Основной.

2. Набор вспомогательных.

Задачу оптимизации в рамках конкретного УУ решают по основному критерию. По полученным оптимальным параметрам определяют величины вспомогательных критериев. Качество системы оценивают по совокупности.

Один из главных критериев – устойчивость системы:

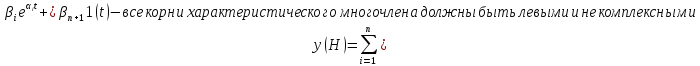
Алгебраические критерии устойчивости Критерий Гурвица

Рассмотрим характеристический полином.

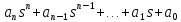
Необходимым условием является, чтобы все корни были одного знака.

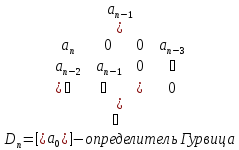
Алгоритм построения:

1. По главной диагонали выставляются все коэффициенты характеристического уравнения.

2. От каждого элемента диагонали влево и вправо достраиваются строки определителя так, чтобы:

   1. Вправо индексы убывают.

   2. Влево индексы увеличиваются.

3. На место коэффициентов с индексами меньше нуля или больше ставятся нули.

Для того чтобы система была устойчива (все корни характеристического полинома лежал в левой полуплоскости) необходимо и достаточно, чтобы все 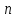дополнительных миноров определителя Гурвицабыли положительными. Эти миноры называются определителями Гурвицапорядка.