4.

1 arctg

x + 2

+C . 5.

2ln(x2 +3x + 4) −

18

arctg

2x +3

+C .

5

5

2x −1

7

7

6.

3 ln

x2

− x +1

+

1

arctg

+C .

2

3

3

С

1)

∫

1

dx

;

∫

dx

;

∫

dx

; ∫

dx

.

x

2

2

5 − x

2

+16

x +

6

15 − x

x2

x

+ 2x3

3

x

1+3cos3 x

5

2)

∫

dx ; ∫

(5x

− 4x + 6

)dx ;

∫

cos2 x

dx;

∫(3 − x)dx.

x

dx

5

x

3

3)

∫2

5x2 +2x+3

(5x +1)dx ;

∫

;

∫

dx;

ctgxdx

.

x 3

∫

ln x

x

sin2 x

4)

∫(1−6x)sin xdx ;

∫x3 ln xdx ;

∫e2x+1 (x −5)dx .

5)

∫sin 3xsin 2xdx ; ∫cos

2

3x

dx .

8

1)

∫

2xdx

;∫

dx

;∫

dx

;∫

dx

.

x2 +5

5 − x2

x2 +6

x2 + 2

(

+

2)2 dx;∫(8x3 −4x + 3

2dx

−

1

2) ∫

x

)dx;∫(

)dx .

x

x3

x

sin2 x

∫

(tgx −5)7

∫

ln(x + 6)

dx; ∫

cos xdx

; ∫e

2x2

+1

xdx .

3)

dx;

x + 6

cos2 x

2sin x +1

Вариант 3

И

1)

∫

3xdx

;∫

dx

;∫

dx

;∫

dx

.

x2 +7

10 − x2

x2 −1

8 − x2

4 − 3

x2

1

2

2)

∫

dx;∫(

+

)dx;∫(2

x +3)3 dx .

x

cos2

x

x4

3

3

2

cos xdx

Д

3) . ∫

;∫53x

+1 xdx;∫ ln

(x +5)dx;∫

x dx

.

sin x

−

5

x +5

3

−

x

4

4)

∫(5x + 6)cos xdx ;

А

2 + 2)exdx .

∫ln3x dx ;

∫(x

x

3x

2x

б

5)

∫sin

cos

dx ;

∫sin

2

2x

dx.

3

2

5

и

Сdx dx

Вариант 4

1)

dx

dx

.

∫

;

∫

;

∫

;∫

x2 +6

16 − x2

x2 +

3

7 − x2

2) ∫

2 + 5

x3

dx;∫(

1

+

2

)dx;∫(3

−5)2 dx .

x

x

x4

3 x

2 + arctg5x

x2dx

3)

∫

ln(x +1)

dx;

∫

dx; ∫ xcos(3x

2

−5)dx;∫

.

x +

1

1 + x2

x3

+ 2

a < b , и

если

1)

разбить отрезок [a b;] произвольным образом на n частичных

отрезков

длиною

∆xi

(i = 0,1,2,..., n),

так

что

произвольной точке с ,с ,...,c ;

1 2

n

3)

вычислить значения функции f (x) в выбранных точках;

4)

составить сумму произведений вида

ДИ

,

то она

отрезке

[a b;].

Очевидно, что при различных разбиениях отрезка [a b;] на части

образом, для данной функции f (x) и данного отрезка [a b;]

можно

А

б

и

составить бесконечное множество интегральных сумм σn , которые

зависят от числа разб

ен й n и от выбора точек деления xi

и точек

ci [xi−1; xi ].

При этом оказывается, что

все эти

различные

интегральные

суммы

при неограниченном

возрастании

n

и при

отрезка, [a b;] таких, что λ = max ∆ xi → 0 (n → ∞), при любом выборе

точек

ci [xi−1; xi ] интегральная сумма

n

σn = ∑ f (ci )∆xi стремится к

i=1

∑ f (ci )∆xi = A ,

одному и тому же конечному числу A:limσn

= lim

λ→0

λ→0

n=1

Итак, по определению,

b

n

∫ f (x)dx = lim

∑ f (ci )∆xi .

a

λ→0

i=1

Числа

a

и b называются

пределами

интегрирования:

a −нижним,

b −верхним.

Отрезок

[a b;] называется отрезком

интегрирования.

Функция

f (x)

называется

подынтегральной

функцией, а переменная x −переменной интегрирования.

Свойства определенного интеграла

1.

Интеграл от алгебраической суммы функций равен

алгебраической сумме интегралов от всех слагаемых:

b

b

b

∫[f

(x)± g(x)]dx = ∫ f (x)dx ± ∫g(x)dx .

a

a

a

2.

При перестановке пределов интегрирования меняется знак

интеграла:

b

a

(x)dx .

∫ f (x)dx = −∫ f

a

b

И

3.

Интеграл с одинаковыми пределами равен нулю:

b

Д

∫ f (x)dx =

0 .

b

4.

А b

b

Если f (x)≥ g(x) при всех x [a;b], то ∫ f (x)dx ≥ ∫g(x)dx .

5.

б

a

a

Если m ≤ f (x)≤ M при всех x из промежутка [a b;], то

и b

m(b − a)≤ ∫ f

(x)dx ≤ M (b − a).

a

6.

ОтрезокСинтегрирования можно разбивать на части:

b

c

b

(x)dx , с (a,b).

∫ f (x)dx = ∫ f (x)dx + ∫ f

a

a

c

7.

Постоянный множитель можно выносить за знак интеграла:

b

b

∫kf (x)dx = k∫ f (x)dx ( k −постоянная).

a

a

Для вычисления определённого интеграла, когда можно найти

соответствующий неопределённый интеграл,

применяется формула

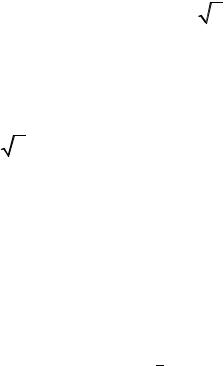
b

∫ f (x)dx = F(x)

b

= F(b) − F(a).

a

a

3

4

−4x +

x

Пример 1. Вычислить ∫

1

2

dx.

1

4

3

x

4

4

3

4

1

∫ 1−4x +

2

dx =

∫dx −4∫ x dx +

2

∫ x2 dx =

1

1

1

1

1

= x|

4

−4

x2

|

4

+

3 x2+1

|

4

=

2

2

1

1

1

+1

1

2

3

−12 )

3 3

= 3 −30 +7 = −20.

= x|14 −2x2|14 + x2 |14 = (4 −1)−2(42

+

42 −12

4

x

И

Д

затем разложим интеграл на сумму интегралов и применим формулу

и1

x

Ньютона – Лейбница

А

4

4

x

4

4

x

x

x

4

4

4

∫(1+e

С

= 4 + 4e −4 = 4e .

)dx = ∫dx + 4∫бe d = (x + 4e )

0

0

0

4

0

Пример 3. Вычислить ∫(3x2 +

1

2

)dx .

−

x2 +1

ln 2

0

Решение. Разложим определенный интеграл на сумму

табличных интегралов и получим следующее:

1

2

1

2x

1 2

1

dx

1

1

x

∫(3x

+

−

)dx

= 3∫ x

dx

+ ∫

−

∫

2

dx =

x2 +1

ln 2

x2 +1

ln 2

0

0

0

0