
- •ВВЕДЕНИЕ
- •1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- •§1. Основные понятия теории функции нескольких переменных
- •§2. Частные производные функции нескольких переменных
- •§3. Элементы скалярного поля
- •§4. Экстремум функции двух переменных
- •Вопросы и задания для самопроверки
- •2. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
- •§ 1. Первообразная функция и неопределенный интеграл
- •§ 2. Замена переменной в неопределенном интеграле
- •§ 4. Интегрирование тригонометрических функций
- •Вопросы и задания для самопроверки
- •3. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
- •§ 2. Методы вычисления определенного интеграла
- •§ 3. Приложения определенного интеграла
- •§4. Несобственные интегралы с бесконечными пределами
- •Вопросы и задания для самопроверки
- •Контрольная работа по теме «Определённый интеграл»
- •4. ДВОЙНОЙ ИНТЕГРАЛ
- •§2. Замена переменных в двойном интеграле
- •Вопросы и задания для самопроверки
- •Контрольная работа по теме «Двойной интеграл»
- •5. ЭЛЕМЕНТЫ ТЕОРИИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- •§1. Основные понятия теории дифференциальных уравнений
- •§4. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Вопросы и задания для самопроверки
- •6. КОМПЛЕКСНЫЕ ЧИСЛА
- •§1. Комплексные числа и действия над ними
- •Контрольная работа по теме «Комплексные числа»

|
9. С какой |
наибольшей скоростью может убывать функция |
||||||||||||||||
u = ln(x2 − y2 + z2 ) |
при |
переходе |
точки |
M (x, y, z) |
через |
точку |
||||||||||||
M0 (1;1;1) ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Ответы |
|
|
|
|
|
|
|
|
|||
|
1. x2 + 2y = 3 |
парабола. |
2. 3. |
3. |
|
grad z(M ) |
|
= 1 . |
4. 0. |
5. 12 . |
||||||||
|
|
|
||||||||||||||||
|
5 + 4 |
|
. |
7. 3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6. − |
2 |
. 8. (−3;1) и (1;−1). |
9. 2 |
|
|
. |
|
|
|
|
||||||||
3 |
|
|
|
|
||||||||||||||
|
2 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§4. Экстремум функции двух переменных |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
И |
M0 называется |
|||||||
|
Значение |
функции |
z = f (x, y) |
|
в |
|
|
точке |
||||||||||
максимумом |
(минимумом), |
|
Д |
является |
наибольшим |
|||||||||||||
если |
оно |
|
|
|||||||||||||||
(наименьшим) по сравнению с её значениями во всех достаточно
близких точках. |
А |
Необходимые условия существования экстремума функции двух |
|
переменных. Функция z = f (x, y) может иметь экстремум только в тех |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
точках, лежащих внутри о ласти определения функции, в которых |
|||||||||||||||||||
∂f = 0 |
и |
|
∂f |
|
|
= 0. Эти точки называются стационарными. |
|||||||||||||
∂x |
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
||||
Достаточные услов я существования экстремума функции двух |
|||||||||||||||||||
переменных. |
Обознач м через |
|
A, |
B |
и |
C значения частных |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
и |
∂2 f |
∂2 f |
|
∂2 f |
|
|||
производных второго порядка |
∂x2 , |
∂x∂y |
и |
∂y2 |
в стационарной |
||||||||||||||
точке M |
0 |
(x , y ) . |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
0 |
С0 |
|
|
|
|
|
|
|
||||
Тогда, если |
|
|
|
|
|
|
|
|
|
||||||||||
1) |
|
|
A B |
|
> 0, |
то функция имеет экстремум в стационарной точке, |
|||||||||||||
|
|
|
|||||||||||||||||
|
|
|
BC |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
f (x , y ) = z |
|
при A < 0; |
|
|
|
|
|
|||||||||
причём |
|
|
|
|
|
0 |
0 |
max |
|
|
|
|
|
|
|
||||
|
|
|
f (x0 , y0 ) = zmin при A > 0; |
|
|
|
|
|
|||||||||||
2) |
|
|
A B |
|
|
< 0, |
то экстремума нет; |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
BC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
16

3) BACB = 0, то требуются дополнительные исследования (экст-
ремум функции может быть, а может и не быть).
Пример 1. Найти экстремум функции z = x3 +8y3 −6xy +5 . Решение. Находим частные производные первого порядка z′x , z′y
и точки, в которых они равны нулю или не существуют и которые
лежат |
внутри |
|
области |
|
определения |
функции: |
z′x = 3x2 −6y ; |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z′ |
= 0; |
|
|
|
|
|
|
z′y = 24y2 −6x . |
Решая систему уравнений вида |
|
x |
|
найдём две |
||||||||||||||||||
|
|
= 0, |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z′y |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точки |
M1(0;0) |
|
|
|
|
|
Обе |
точки |
являются |
стационарными. |
|||||||||||||
и M 2 1; |
2 |
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Далее |
исследуем |
точки |
|
по |
|
знаку |
определителя |
∆ = |
|
AB |
|
, |
|||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BC |
|
|
составленного |
|
из |
частных |
производных |
второго |
порядка: |
|||||||||||||||||
′′ |
= 6x |
; |
′′ |
|
|
|
|
|
|
′′ |
|
|
|
|
И |
|
|
|
|
|
|
||
zxx = A |
zxy = B = −6; |
|
zyy = C = 48y . |
|
|
|
|
|
|
||||||||||||||
Для |
точки |
M1 |
|
|
получим |
A = 0; |
B = −6 ; |
C = 0 |
|
и |
|||||||||||||
∆(M1) = AC − B |
2 |
= −36 < 0 . |
|
|
|
|
Д |
в |
точке |
M1 |
|
нет |
|||||||||||
|
Следовательно, |
|
|||||||||||||||||||||
экстремума. |
|
|
|
|
|
|
|
|
|
А |
C = 24 и ∆(M 2 ) =108 > 0. |
||||||||||||
Для точки M 2 |
меем |
|
A |
||||||||||||||||||||
|
= 6 |
; |
B = −6 ; |
||||||||||||||||||||
Согласно достаточному услов ю существования экстремума, M 2 |
|
есть |
|||||||||||||||||||||
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|||||
точка минимума. zmin = z(M |
2 ) |
= 4. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пример |
|
|
2. |
иИсследовать |
на |
экстремум |
функцию |
||||||||||||||||
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z = x3 + y2 −3x + 4
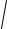 y5 .
y5 .
Решение. Найдём область определения данной функции. Это все точки M (x, y) , координаты которых удовлетворяют системе
неравенств |
−∞ < x < +∞; 0 ≤ y < +∞. |
Найдём |
частные производные |
||||
первого порядка |
∂z = 3x2 −3; |
∂z |
= 2y + 2 |
|
|
систему |
|
y3 . Решая |
|||||||
|
|
∂x |
∂y |
|
|
|
|
|
z′ = 0; |
|
|
|
|
|
|
уравнений |
x |
найдём две точки |
M1(1;0) |
и M2 (−1;0), |
которые |
||
|
|||||||
|
z′y = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лежат не внутри области определения функции, а на её границе y = 0.
17
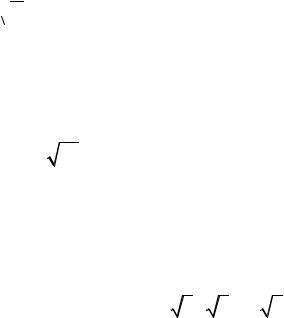
Поэтому точки M1 и M2 не являются стационарными и данная функция не имеет экстремума.
Задачи для самостоятельного решения
Исследовать на максимум и минимум функции:
1 z = x2 + y2 − xy +9x −6y + 20. 2. z = 3x + 6y − x2 − xy − y2 .
3. z = x
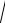 y − x2 − y + 6x + 3.
y − x2 − y + 6x + 3.
4. z = x3 y2 (6 − x − y) .
5. z = x2 + xy + y2 + |
1 + |
1 |
. |
|
|
|
|
|
|
|
|
|
И |
||||||||||
y |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||
6. z = x3 + y3 −3xy . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
7. z = (x2 + y) ey . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ответы |
|
|
|
|
|
|
|
|||||
1. |
z |
|
|
|
|
|
б |
|
|
9 |
|
. 3. z |
|
|
= z(4;4) =15. |
||||||||
|
|
min |
|
|
|
|
|
|
min |
|
|
|
|
Д |
max |
|
|||||||
4. zmax |
= z(3;2) =108. 5. |
zmin = z( |
1 |
|
; |
1 |
) = |
|
9 |
. 6. |
zmin = z(1;1) = −1. |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
и |
А3 3 |
3 |
9 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
||
7. zmin |
= z(0;−2) = − |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вопросы и задания для самопроверки |
||||||||||||||||||||
1. Сформулируйте понятие функции нескольких переменных и |
|||||||||||||||||||||||
её предела. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. |
Какая |
функция |
|
нескольких |
|
переменных называется |
|||||||||||||||||
непрерывной? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.Как определяются частные и полное приращения функции двух переменных в точке?
4.Дайте определения частных производных первого порядка.
5.Приведите уравнения касательной плоскости и нормали к поверхности.
6.Как определяются частные производные высших порядков?
18

7.Сформулируйте понятие полного дифференциала функции нескольких переменных и укажите его применение для приближенных вычислений.
8.Дайте определение скалярного поля, линий уровня, поверхностей уровня.
9.Что называется производной по направлению?
10.Определите, что такое градиент и укажите его свойства.
11.Что называется экстремумом функции нескольких пере-
менных?
12.Сформулируйте необходимые и достаточные условия существования экстремумов функции в точке.
|
|
|
Контрольная работа по разделу «Функции нескольких |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
переменных» |
И |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1. |
Найти область определения функции z = y + |
x |
. |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
1 |
|
|
|
|
3y |
|
|
|||
|
|
|
2. |
Найти частные производные функции z = |
|
|
arctg |
|
. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
4x3 |
|
|
||
|
|
|
3. |
Найти |
, |
|
если |
дана |
сложная |
|
функция |
u = e |
z2 −y2 |
, где |
||||||||||||||||
|
|
|
|
|
|
|
|
|
dx |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
z = cos x; |
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y = sin x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
4. |
|
|
Найти |
|
|
∂z |
|
и |
|
∂z , |
|
если |
дана |
неявная |
|
функция |
|||||||||||
|
|
( |
|
|
|
|
) |
|
|
|
∂x |
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
С2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
sin |
|
x + y |
|
−sin |
2 z |
+cos |
2y = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
z = |
x |
|
|
|
|
|
|
|
|
1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
5. |
Найти градиент функции |
|
|
в точке |
M0 1; 2; |
|
. |
||||||||||||||||||||
|
|
|
x2 + y2 |
5 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6. |
Составить уравнения касательной плоскости и нормали к |
поверхности z = x2 + y2 в точке B(1; 2; 5). |
|
7. |
Найти частные производные второго порядка функции |
z = ctg(3x y).
8. Исследовать на экстремум функцию z = x2 + 2xy −4x −8y .
19
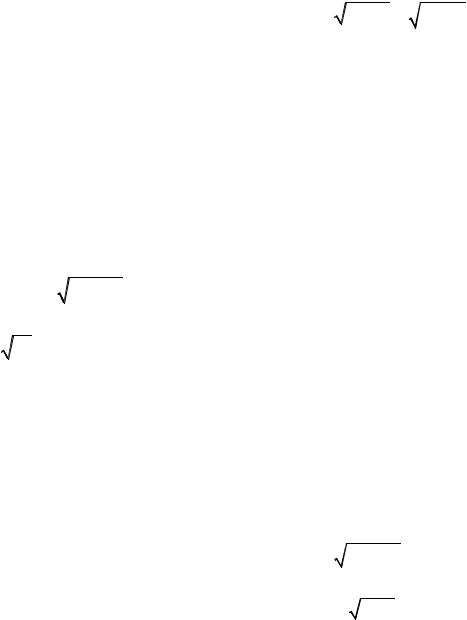
9. |
Найти |
|
|
наибольшее |
и наименьшее |
|
значения |
функции |
|||||||||||||||||||||||||
z = −x2 + xy − y2 −9y +6x |
в замкнутой области, ограниченной линиями |
||||||||||||||||||||||||||||||||
y = −x; x = −2; y = −6 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. |
Найти область определения функции z = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
x2 −4 + |
4 − y2 . |
||||||||||||||||||||||||||||||
2. |
Найти частные производные функции |
z = |
|
|
5x2 −2y . |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x +3y |
|
|
|
|
|
|
|||||||
3. |
Найти |
|
∂z |
|
и |
∂z |
, |
если |
z = uv , |
где |
u = sin x; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∂u |
∂v |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ν = cos x. |
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||
|
|
|
|
|
∂z |
|
∂z |
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
||||||||||
4. |
Найти |
|
∂x |
и |
∂y |
, если дана неявная функция y3 − x2 = arctg |
|
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|||||
5. |
Найти |
|
|
градиент |
функции |
z = 3x2 y −3xy2 + y4 |
|
в точке |
|||||||||||||||||||||||||
M (1; 2; 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6. |
Составить уравнения касательной плоскости и нормали к |
||||||||||||||||||||||||||||||||
|
|
|
|
|
A(3; 4; 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
поверхности z = |
x2 + y2 |
− x в точке |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
7. |
Найти |
частные |
б |
|
|
|
|
|
|
порядка |
функции |
||||||||||||||||||||||
производныеДвторого |
|
|
|
||||||||||||||||||||||||||||||
z = xy (1− |
|
). |
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
xy |
|
|
|
|
|
|
|
|
|
2 |
+ 2xy + 4x |
− y |
2 |
. |
|
|
|||||||||||||||||
8. |
Исследовать на экстремум функцию z = x |
|
|
|
|
|
|
||||||||||||||||||||||||||
9. |
Найти |
на большее и наименьшее значения функции |
|||||||||||||||||||||||||||||||
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
z = x2 + y2 +6x |
+ |
2y |
|
в замкнутой области, ограниченной линиями |
|||||||||||||||||||||||||||||
x = −5; y = x; y = 0. |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. |
Найти область определения функции z = |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
y sin x |
|
|
|
|
|
|
||||||||||||||||||||||||
2. |
Найти частные производные функции |
z = |
|
|
|
2xy |
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
sin x |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. |
Найти |
|
dz |
, |
если |
|
z = arcsin(x − y), |
где |
x = 3t; |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
y = 4t3. |
|
|
|
|
|
|
||||||||||||
4. |
Найти |
|
dy , если дана неявная фунция y3 − xy = ln |
x |
|
. |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
||||||
20
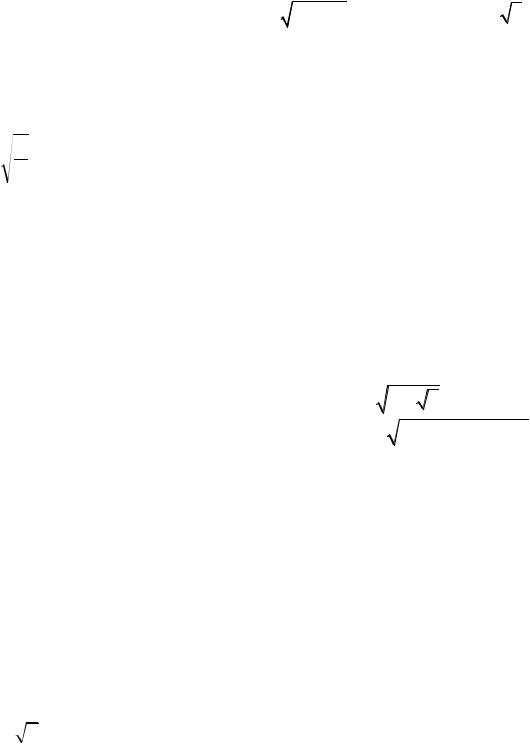
5. |
Найти градиент функции z = 3 |
|
в точке M (1;1; 3 |
|
). |
||||
x2 + y2 |
|||||||||
2 |
|||||||||
6. |
Составить уравнения касательной плоскости и нормали к |
||||||||
поверхности z = |
x2 |
− y2 в точке |
N (2; −1; 1). |
||||||
|
|||||||||
7. |
2 |
|
|
|
|
|
|
||
Найти частные производные второго порядка функции |
|||||||||
z = ln 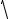
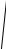 xy .
xy .
|
|
|
8. |
Исследовать на экстремум функцию |
z = x2 + xy + y2 + x − y +1. |
|||||||||||||||||||||
|
|
|
9. |
Найти |
|
наибольшее и |
наименьшее |
значения |
функции |
|||||||||||||||||
z = x2 +3xy + y2 −3x −2y |
|
|
в замкнутой области, |
|
ограниченной линиями |
|||||||||||||||||||||
y = −x; y = 2; x =1. |
|
|
|
|
|
|
|
|
И |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 4 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
1 |
|
|
|
|
|||||
|
|
|
1. |
Найти область определения функции |
z = |
|
y − |
|
. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2. |
Найти частные производные функции z = 3 |
1+ 4xy + x2 +3y3 |
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
t |
; |
|
|
|
|
|
|
|
|||
|
|
|
3. |
Найти |
|
dz |
, |
|
если |
z = |
x |
, |
где x = e |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
y |
y = lnt. |
|
|
|
|
|
|
|||||
|
|
|
4. |
Найти |
|
∂z |
|
|
∂z , |
если |
|
|
неявная |
функция |
||||||||||||
|
|
|
|
|
|
|
|
∂x |
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ln |
( |
x2 |
+ y2 + z2 |
) |
+ arctg |
y2 |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
иx |
|
|
|
|
|
|
|
A(1; 2; 4). |
||||||||||||
|
|
|
5. |
Найти градиент функции z = 2x2 + xy |
в точке |
|||||||||||||||||||||
|
|
|
6. |
Составить уравнения касательной плоскости и нормали к |
||||||||||||||||||||||
поверхности z = xy |
в точке |
(−1; −1; 1). |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
7. |
Найти |
частные производные второго |
|
порядка |
функции |
||||||||||||||||||
z =sin(
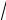 x + y).
x + y).
8. Исследовать на экстремум функцию |
z = x2 + y2 −12x +16y . |
|||
9. Найти |
наибольшее и |
наименьшее значения |
функции |
|
z = 27x −6y − x3 + y2 |
в замкнутой |
области, |
ограниченной |
линиями |
x + y = 5; y − x = 5; y = 0.
21
