Вопросы и задания для самопроверки

Вопросы и задания для самопроверки

5. ЭЛЕМЕНТЫ ТЕОРИИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

§1. Основные понятия теории дифференциальных уравнений

Контрольная работа по теме «Двойной интеграл»

5. ЭЛЕМЕНТЫ ТЕОРИИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

§1. Основные понятия теории дифференциальных уравнений

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1791.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.83 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1613 14 15 16 > Следующая >>>

Ответы

1. 2π 3 . 2. 54 . 3. 1283π . 4. −6π 2. 5. 9π 6. 28π . 7. 4π −3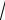3 . 8. 1.

1.	Сформулируйте задачи, приводящие к понятию двойного
интеграла.
2.	Сформулируйте определение двойного интеграла									и укажите
его свойства.
3.	Укажите формулу для вычисления двойного интеграла путём
двухкратного интегрирования в декартовых координатах.
4.									И
4.	Укажите формулу для вычисления двойного интеграла в
полярной системе координат.						Д
5.	Какие геометрические и механические приложения двойного
интеграла вы знаете?					А
					А
	Контрольная работа по теме «Двойной интеграл»
			и		Вариант 1
1.			и
1.	Изменить порядок нтегрирования
		−1	0	б		0	0		f (x; y)dy .
		∫	dx ∫	f (x; y)dy + ∫ dx ∫					f (x; y)dy .
		−2 −2−x				−1	3
		−2 −2−x				−1	3	x
2.	Вычислить		∫∫(2xy − x2 )dxdy ,				где область D			ограничена
			D
линиями y = 0;Сy = 2; y = x; y = x −4.
3. Переходя к полярным координатам, найти с помощью
двойного		интеграла		площадь,					ограниченную	линиями

x2 −4x + y2 = 0; x2 −8x + y2 = 0; y = 0; y = x.

4. Найти с помощью двойного интеграла координаты центра тяжести фигуры, ограниченной линиями x =1; y = 0; y2 = 4x; y ≥ 0, если поверхностная плотность µ(x, y) = x2 y .

Вариант 2

1. Изменить порядок интегрирования

f (x; y)dx .

∫dy 2∫ f (x; y)dx +

∫dy ∫

2. Вычислить ∫∫(x2 + y)dxdy ,

где область D ограничена линиями

x =1; y = x; xy =1; x = 2 .

3. Переходя

полярным

координатам, найти с помощью

двойного

интеграла

площадь,

ограниченную

линиями

x2 −6x + y2 = 0; x2 −4x + y2 = 0; y = 3x, x = 0.

4. Найти с помощью двойного интеграла координаты центра

тяжести

фигуры,

ограниченной

линиями

x +3y = 0; y2

= 4 + x, если

поверхностная плотность µ(x, y) = y .

Вариант 3

1. Изменить порядок интегрирования

2−y2

f (x; y)dx

∫dy∫

+ ∫

∫

f (x; y)dx .

2. Вычислить

∫∫

(2y − x)dxdy , где область D ограничена линиями

y = x; x = 4; xy = 4.

киполярным

3. Переходя

координатам, найти с помощью

двойного

интеграла

площадь,

ограниченную

линиями

x2 −2x + y2 = 0; x2 −6x + y2 = 0; y = 0; y = x .

4. Найти с помощью двойного интеграла координаты центра тяжести фигуры, ограниченной линиями y = x; y = x2 −2x , если поверхностная плотность µ(x, y) = x + y .

Вариант 4

1. Изменить порядок интегрирования

1	y	2	2−y	f (x; y)dx .
∫dy∫		f (x; y)dx + ∫dy	∫	f (x; y)dx .
0	0	1	0


2.	Вычислить			∫∫(2y − x2 )dxdy ,		где область D	ограничена
линиями 2y = x2 ;				D
линиями 2y = x2 ;			x = y
3.	Переходя		к	полярным координатам, найти			с помощью
двойного		интеграла			площадь,	ограниченную	линиями

x2 + 2x + y2 = 0; x2 +6x + y2 = 0; y = 0; y = −x .

4. Найти с помощью двойного интеграла координаты центра тяжести фигуры, ограниченной линиями yx = 4; y + x = 5 , если

поверхностная плотность µ(x, y) = x −2y .

моделирования сводится к отысканию неизвестнойИ функции из уравнения, содержащего независимую переменную, искомую

Решение различных задач методом математического

функцию и производные этой функции. Такое уравнение называется
дифференциальным.		Д
Решением	дифференциального
уравнения называется всякая функция,
		А
которая обращает данное уравнение в
тождество. Приведем пр бмер, приводящий
к дифференциальному уравнен ю.
Рассмотрим	изадачу	нахождения
функции, график	которой	обладает тем	А
свойством, что отрезок любой касательной,
С			Рис. 5.1
заключенной между осями координат,
делится пополам в точке касания.

Пусть y = f (x) – искомая функция, а M (x, y)– произвольная

точка кривой, определяемой этим уравнением; предположим для определенности, что кривая расположена в первой четверти (рис. 5.1). По условию задачи, имеем BM = MA, следовательно, OP = PA = x . Из

рис. 5.1 видно, что tg ( PAM )=			MP	, т.е.	tg (180 −α)=	y	, или
рис. 5.1 видно, что tg ( PAM )=			PA	, т.е.	tg (180 −α)=	x	, или
	y		PA			x
− tg α =	y	.
− tg α =		.
	x

Учитывая,

что

tg α

есть угловой коэффициент касательной,

который

в точке M (x, y)

равен

y′,

получаем дифференциальное

уравнение

′

= − x

вида y = C

решением

которого

является

всякая

функция

где C –

произвольная постоянная.

y = C ,

В самом деле,

заменив в

уравнении

на функцию

получим

C ′

= −

, т.е. −

= −

y = C

Следовательно, равенство

определяет

множество

функций,

обладающих

указанным

задаче

свойством. Графики этих функций

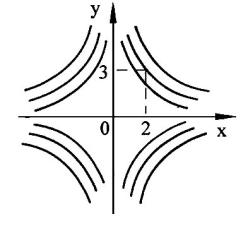
представляют собой семейство гипербол

(рис. 5.2).

АДифференциальным уравнением

называется уравнение,

содержащее

Рис. 5.2

независимую переменную x , искомую

функцию

ее

производные

y′, y′′, , y(n) [3].

имволически дифференциальное

уравнение

записывается так:

′

(n)

)= 0.

F(x, y, y

, , y

Порядком дифференциального уравнения называется

порядок

высшей производной, содержащейся в данном уравнении.

Дифференциальным

уравнением

первого

порядка

называется уравнение вида

F(x, y, y′)= 0.

Разрешая последнее уравнение относительно производной y′,

если это возможно, получим

(x, y).

y′ =

Рассмотренный выше пример показывает, что дифференциальное уравнение имеет, вообще говоря, бесконечное множество решений.

При различных значениях постоянной C равенство y = Сх определяет различные решения уравнения y′ = − ух.

соответствует, как правило, бесконечная совокупность его решений. Всякое отдельно взятое решение дифференциального уравнения

называется его частным решением. С геометрической точки зрения совокупность всех решений дифференциального уравнения представляет собой семейство кривых, называемых интегральными кривыми, а каждое частное решение представляет отдельную

интегральную кривую.		называетсяИобщим
Функция	y =ϕ(x,C)		решением


дифференциального уравнения первого порядка, если при любом
значении C эта функция является решениемДуравнения и любое его
частное решение может		ыть получено из y =ϕ (x,C) при некотором
	и		А
значении постоянной C .
В некоторых случаях не удается получить решение
дифференциального уравненбя в явной				форме y =ϕ (x)	или
y =ϕ (x,C), а получают		х в неявной форме, т.е. решение задается
формулой вида	Ф(x, y)= 0, или Ф(x, y,C)= 0.

ВыражениеСФ(x, y)= 0, или Ф(x, y,C)= 0				в этом случае называют

интегралом (частным, общим) дифференциального уравнения.

При решении конкретных задач часто необходимо выделить из всей совокупности решений дифференциального уравнения то частное решение, которое является ответом на поставленный вопрос. Для того чтобы из всей совокупности решений выделить отдельную интегральную кривую, задают так называемое начальное условие.

В случае дифференциальных уравнений первого порядка под начальными условиями для его решения y = y(x) понимают условия,

состоящие в том, что y = y0 при x = x0 , т.е.

y(x0 )= y0 ,

где x0 и y0 – заданные числа (начальные данные), такие, что при

x = x0 и y = y0 функция имеет смысл, т.е. существует f (x0 , y0 ). Задача нахождения частного решения дифференциального

уравнения, удовлетворяющего заданным начальным условиям, называется задачей Коши.

В случае дифференциального уравнения первого порядка задача Коши формулируется следующим образом: найти решение y = y(x)

уравнения y′ = f (x, y), удовлетворяющее при заданных начальных данных (x0 , y0 ) начальному условию y(x0 )= y0 , где x0 , y0 – заданные числа.

Пусть даны начальные данные x0	= 2; y0 = 3					и требуется найти
частное решение y = y(x) уравнения	y	′		y	,		удовлетворяющее
			= − x

начальному условию y(2)= 3. Подставим						в	функцию y = C ,
							x

являющуюся решением данного уравнения,Иначальные данные x = 2 ; y = 3. Получаем, что 3 = C / 2, т.е. C = 6. Таким образом, искомым

частным решением уравнения является функция				y = 6 / x .
	б			начальному условию
Геометрически решение, удовлетворяющееД
y(x0 )= y0 , представляет интегральную кривую, проходящую через
и			А
данную точку (x0 , y0 ).					′
Так, общее решен е		y = C / x уравнения y				= −y / x определяет

семейство равносторонн х г пербол (см. рис. 5.2). Частное решение y = 6 / x определяет гиперболу, проходящую через точку (2;3).

§2. Дифференциальные уравнения
С	первого порядка

Рассмотрим различные типы дифференциальных уравнений первого порядка и методы их решения.

Дифференциальные уравнения первого порядка с разделяющимися переменными

Дифференциальное уравнение называется уравнением первого порядка с разделяющимися переменными, если оно имеет вид

y′ = f1(x) f2 (y)

или

f1(x) g1(y)dx + f2 (x) g2 (y)dy = 0.

Для дифференциального уравнения первого порядка с разделяющимися переменными теорема Коши о существовании и единственности решения может быть сформулирована следующим образом.

Теорема. Если функция f1(x) непрерывна в интервале (a b;), функция f2 (y) и ее производная по y непрерывна в интервале (c;d ), то для любых начальных данных x0 (a;b), y0 (c;d ) существует, причем единственное, решение y =ϕ(x) уравнения y′ = f1(x) f2 (y), удовлетворяющее начальному условию ϕ(x0 )= y0 .

Другими словами, при указанных условиях через любую точку

прямоугольника a < x < b, c < y < d

проходит,

при том

единственная, интегральная кривая уравнения.

Если f2 (y)≠ 0, то уравнение

y′ = f1

(x) f2

(y) можно переписать

в виде (разделить переменные)

= f

(x)dx.

f2 (y)

Последнее уравнение называется уравнением с разделёнными

переменными.

Теорема. Если существуют интегралы ∫

∫ f1(x)dx, то

f2 (y)

общий интеграл уравнен я с разделенными переменными задается уравнением

	F (y)				F2 (y)= F1 (x)+C ,
где			и СF (x) – некоторые первообразные соответственно
	2		1
функций			1	и	f1(x).
		f2 (y)

При решении дифференциальных уравнений с разделяющимися переменными можно руководствоваться следующим алгоритмом:

1)разделить переменные;

2)интегрируя обе части полученного уравнения с разделёнными переменными, найти его общий интеграл;

3)найти частный интеграл (или частное решение), удовлетворяющий начальным условиям (если это требуется).

Однородные дифференциальные уравнения первого порядка

Функция g(x, y) называется однородной функцией k -го

порядка, если при любом t имеет место тождество

g (tx,ty)= tk

g (x, y) .

Например,

g(x, y)= 2x3 −5xy2

– однородная функция третьего

порядка, т.к.

g(tx,ty)= 2(tx)3 −5tx(ty)2 = 2t3 x3 −5t3 xy2 =

= t3 (2x3 −5xy2 )= t3 g(x, y).

частности,

функция f (x,

называется

однородной

функцией нулевого порядка, если

при

любом t

справедливо

тождество

f (t x;

t y)=

f (x, y).

Так,

функция

f (x, y) =

3x + y

является однородной

функцией

x − y

tИсправедливо тождество

нулевого

порядка,

так

как

при любом

f (tx,t y)=

3tx +ty

= t(3x + y)

= f (x, y).

tx −ty

t(x + y)

′

= f (x, y)

Дифференциальное

уравнение

первого порядка

называется однородным, если Аf (x, y) является однородной функцией

нулевого порядка.

Например,

д фференц альное

уравнение

первого

порядка

3x + y

будет однородными.

y′ = x − y

Замечания:

ДифференциальноеС

уравнение первого порядка

y′ = f (x, y)

является однородным, если функцию

f (x, y)

можно представить как

функцию только одного отношения переменных

f (x, y)

= g(

) , т.е.

′

уравнение

можно

преобразовать к

виду y

= g( x ).

Затем делаем

′

замену

x = t; y

= t

x +t

и получаем дифференциальное уравнение

первого порядка с разделяющимися переменными: t′ x +t = g (t).

2. Чтобы проверить, является ли дифференциальное уравнение

однородным уравнением, нужно	в этом уравнении заменить
x на tx, y на ty. Если после этого t	всюду сократится и получится
первоначальное уравнение, то данное	уравнение – однородное. Далее

вводим новую функцию t , полагая y = t x, y′ = t′ x +t . В результате

подстановки данное уравнение преобразуется к дифференциальному уравнению первого порядка с разделяющимися переменными:

t + x t′ = f (t)или x t′ = f

(t)

−t , или x

= f (t)−t .

Разделив в уравнении переменные, получим

x .

f (t)−t

Затем, интегрируя

обе части,

интеграл

находим

общий

F(t) = ln

+C , в котором надо подставить t =

Линейные дифференциальные уравнения первого порядка

и уравнения Бернулли

( x), где

Уравнение вида

y′+ p(x)y = q

p(x) и

q(x) −

непрерывные функции, называется линейным дифференциальным

уравнением первого порядка. Приведем теорему Коши для

линейных уравнен й первого порядка.
С	в котором функции
Теорема Коши. Пусть (a b;) − интервал,	в котором функции
p(x) и q(x) непрерывны. Тогда для любых x	(a;b) и y (−∞;+∞)

задача Коши с начальными значениями (x0 ; y0 ) имеет единственное решение, т.е. существует единственное решение y = y(x) линейного уравнения y′+ p(x)y = q( x), удовлетворяющее начальному условию

y(x0 )= y0 .

Решение линейного дифференциального уравнения первого порядка будем искать в виде произведения двух функций от x :

y = u(x) v(x) .

Подставив значения y и y′ в линейное уравнение, получаем u′(x) v(x) +u(x) v′(x) + p(x) u(x) v(x) = q(x) .

После группировки двух членов в левой части последнего уравнения будем иметь

′

или

v(x)(u (x) + p(x) u(x)) +u(x) v (x) = q(x) ,

v(du + p u) +u dv

= q .

Выберем функцию u(x) так, чтобы

+ p u = 0.

Разделяя переменные в этом дифференциальном уравнении,

находим

u(x) = e−∫ p(x)dx .

Подставляя

найденное

значение

функции

u(x) в

уравнение

v(du + p u) +u dv

= q

учитывая,

что

du + p u = 0,

получим

u(x) dv = q(x), или dv

= q(x)

, откуда v(x) = ∫ q(x)dx +C .

u(x)

Заменив

равенстве

y = u v функции u

и v найденными

значениями, получим искомое решение yИ= u (x) v(x,C)

линейного

уравнения.

Уравнение

Бернулли

, отличающееся от

y′+ p(xД)y = y q(x)

линейного уравнения тем, что в правую часть входит множителем

некоторая степень y ,

решается так же,

как и линейное. Посредством

подстановки

y = u v

оно

к двум уравнениям с

также

сводится

разделяющимися переменнымиб.

Рассмотренные выше типы дифференциальных уравнений

можно классифицировать в виде табл. 1.

Таблица 1

1.Уравнения с разделяющимися

y′ =

f1(x) f2 (y)

переменными

∫

= ∫ f1(x)dx

f (y)

2. Однородные уравнения

= z(x)= z ; y = x z ;

первого порядка

′ = f

y′ = z + x z′

3. Линейные уравнения

y′ + P(x) y = Q(x)

y = u v;

1-го порядка

y′ = u′xv +uv′x

4. Уравнения Бернулли

y′ + P(x) y = Q(x)yα

y =u v;

y′ = u′xv + uv′x

Пример 1. Найти решение уравнения 3y2 y′ = 5 −4x3 при условии y(1) = 2 .

Решение. Данное дифференциальное уравнение 1-го порядка является уравнением с разделяющимися переменными. Заменяем y′

на

dy ,

получим

3y2 dy

= (5 −4x3 ),

затем умножаем обе его части на

dx .

Интегрируя

обе

части

последнего

уравнения

3y2 dy = (5 −4x3 )dx ,

найдем

∫3y2 dy = ∫(5 −4x3 )dx ,

или

3∫y2 dy = 5∫dx −4∫x3 dx , или 3

4x3

+C , т.е. y3 = 5x − x4 +C .

= 5x −

Подставив начальное значение x0 =1;

= 2, найдем константу

C: 8 = 5 −1+C , т.е. C = 4.

Следовательно,

искомый

частный

интеграл

будет

y3 = 5x − x4 + 4 , или x4 + y3 −5x −4 = 0.

Пример 2. Найти решение уравнения

(x2 + y2 )dx − xy dy = 0 .

Решение. Разрешая это уравнение относительно производной,

получим

2 + y2 )

= xy dy

, или, так как

dy = y′,

то

′

+ y2

= f

= y + x

уравнение

приняло

вид

( x ). Следовательно,

′

= f ( x ) и является однородным уравнением первого порядка.

Сделаем

′

Затем

замену

x = t; y

= t

x +t

получаем

дифференциальное уравнение с разделяющимися переменными

′

x +t = t +t или dx x = t .

Разделим переменные t dt = dxx и, интегрируя, найдём

t2 = ln x +C . 2

Исключая

вспомогательную функцию

t =

окончательно

1 y2

получим

= ln

+C − общий интеграл.

2 x2

′

Пример 3.

Найти частное решение уравнения

y − xy

= y ln y

при условии y(1) = e .

Решение. Вначале устанавливаем, что данное уравнение является однородным:

y′ =

(1−ln

)

+ln

) =

f (

) , затем заменяем функцию y .

= t; y′ = t′ x + t,

Иdx

Полагая

получаем дифференциальное урав-

нение с разделяющимися переменными

x +t = t(1+ln t), или x

= t ln t .

Умножая

обе

его

части

на

выражение

, разделим

xt ln t

переменные

= dx

и интегрируем

t ln t x

бdx

∫

d(ln x)

ln t

= ln

+ln C ; ln t = Cx .

ln x

Возвращаясь к прежней функции y , находим общий интеграл ln xy = Cx .

Подставив в найденное решение начальное условие, найдем ln 1e = C 1, т.е. ln e = C , или C =1.

Итак, искомый частный интеграл будет иметь вид

ln xy = x .

Пример 4. Найти частное решение уравнения xy′− y = x3 , если

y =1/ 2 при x =1.

Решение. Разделив

все

члены

данного уравнения на x ≠ 0 ,

приведем его к виду

′

= x

, т.е. к линейному уравнению.

− y x

Положим y = u v , откуда y

′

= u dx

+ v dx .

Подставим эти значения в уравнение

u dv

+ v du

−u v

1 = x2 .

Сгруппируем члены, содержащие, например v, и вынесем v за

скобку:

−

= x2 .

+ v

Выберем функцию

так,

чтобы выражение в скобках

обратилось в нуль, т.е. чтобы

dx − x

= 0.

Тогда вторую функцию найдём из уравнения

u dv

= x2 .

Решаем первое уравнен е как уравнение с разделяющимися

переменными (при u ≠ 0 ):

иdx

= x

;

x .

Интегрируя обе части уравнения, получим

∫

dx , или ln u = ln x , или u = x.

Подставив это значение в уравнение u dv = x2 , найдем

x dv

= x2 , т.е.

dv = x dx .

Интегрируя ∫dv = ∫ x dx, находим вторую неизвестную функцию

v = x2 +C .

Заменив в подстановке y = u v функции u и v их выражениями, получим искомое общее решение данного уравнения:

y = x x22 +C , или y = x23 +Cx .

Найдем частное решение, удовлетворяющее начальным данным

y(1) = 1

Для этого

подставим в

общее решение y =

и x =1,

= 13

получим

+C 1,

или 0 = C .

Искомое частное решение данного уравнения y =

Задачи для самостоятельного решения

Найти решения дифференциальных уравнений. В тех задачах, в

которых

заданы

начальные

условияИ, найти

решения,

удовлетворяющие этим условиям.

2 б2

1. (xy2 + 2x)dx −(4y + x2 y)dy

= Д0 .

2. 2xy e dx +(1

− y)dy = 0.

x(1+ y

)+ e

′

= 0, если y = 0 при x = 0.

′

ydy − 2xy dx.

2xdx

+3ydy

5. (x

+ y)y

′

= y .

y2 + x2 y′ = xyy′.

− y = x cos

y′− yctgx = sin x .

9. xy′ + y = x−10 .

10.

x2 y′− 2xy = −3, если y =1 при x = −1.

11.

y′+

y(1) = 0.

xex

12. y′ + 1x y = sinx x .

13.	x y′+ y = y2 ln x.
	dy	2		3
14.	dx	−		y = (x +1) , если	y = 3 при x = 0.
			x +1

Ответы

1. y2 + 2 = C (4 + x2 ). 2. ex2 +C = ln y + 1y . 3.− xe−x −e−x + arctgy = −1.

4x2 −3

5. y = С еy .

y = С еx .

= С.

= ln

С.

(1+ y2 )2

8. y = (x +С)sin x .

10.

y =

−

+ С .

y = 2x

9x9

11.

y =

−

. 12.

y =

(−cos x +С).

13.

1 = ln x +1+Сx.

ех

xex

14. y =

(x +1)4

+ 5 (x +1)2.

§3. Линейные однородные дифференциальныеД

уравнения

второго порядка с постоянными коэффициентами

Линейным

однородным

дифференциальным уравнением

второго порядка с постояннымиб

коэффициентами называется

уравнение вида

иy′′ + py′ + qy = 0 ,

где p и q – заданные действительные числа.

Теорема Коши для линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами формулируется следующим образом.

Теорема Коши. При любых начальных данных (x0 ; y0 ; y0′ ) задача

Коши имеет, причем единственное, решение, т.е. при любых начальных данных x0 , y0 , y0′ существует единственное решение

уравнения y′′ + py′ + qy = 0 , удовлетворяющее начальным условиям y(x0 )`= x0 ; y′(x0 )= y0′.

Два

решения

y1 (x) и y2 (x) уравнения

y′′ + py′ + qy = 0

называются линейно независимыми на отрезке

[a,b], если их

отношение

на

этом

отрезке

не

является постоянным, т.е. если

≠ const .

y2 есть некоторые функции от x , то определитель

Если

W (y1, y2 )=

y1 y2

′

y1′y2′

= y1 y2

− y y2 называется определителем Вронского,

или вронскианом данных функций.

Теорема.

Если

решения y1 (x)

и y2 (x) уравнения

y′′ + py′ + qy = 0

являются линейно независимыми на отрезке [a,b], то

определитель Вронского W (y1, y2 ), составленный для этих решений,

не обращается в нуль ни в одной точке указанного отрезка.

Теорема (о структуре общего решения). Если

(x) и y2 (x) −

два линейно

независимых

решения

линейного

однородного

дифференциального уравнения второго порядка с постоянными

коэффициентами, то общее решение этого уравнения имеет вид

y = C y (x)Д+C y (x) ,

где C1 и C2 –произвольные постоянные.

называется

линейной

комбинацией

Выражение C1 y1

+C2 y2

функций y1(x)

y2 (x).

решение

линейного

однородного

Чтобы найти

общее

дифференциального уравнения второго порядка с постоянными коэффициентами, достаточно найти два линейно независимых частных решения.

Будем искать эти частные решения уравнения в виде y = e		kx	, где

k=const; тогда y′ = kekx ; y′′ = k 2 ekx .
Подставим выражение для	y, y ′ и y′′ в уравнение и получим
k 2ekx + pkekx + qekx = 0, т.е. ekx (k 2 + pk + q)= 0.
Так как ekx ≠ 0, то
k2 + pk + q = 0 .
Уравнение k2 + pk + q = 0	называется характеристическим

уравнением линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами.

Для составления характеристического уравнения достаточно в дифференциальном уравнении заменить y′′, y′ и y соответственно на

k 2 , k и 1.

Решив

характеристическое

уравнение

по

формуле

− p ±

p2 −

найдем его корни

, а следовательно, и

1,2

частные решения уравнения:

y = ek1x ;

= ek2 x .

При решении характеристического уравнения возможны три

случая.

Случай 1. Корни характеристического уравнения действитель-

ны и различны: k1 ≠ k2 .

В этом случае имеем два частных решения уравнения:

= ek1x и

= ek2 x .

Покажем, что эти решения являются линейно независимыми:

ek1x

= e

(k −k

) x

≠ const .

ek2x

Следовательно, о щее решение уравнения имеет вид

= C e

k1x

k2 x

А1

Случай 2. Корни характеристического уравнения действитель-

ны и равны:

k1 = k

2 = k .

В этом случае непосредственно находим лишь одно частное

решение: y

= ekx .

Будем искать второе частное решение в виде y2 = xekx .

Действительно,

′

)

′ kx

+ x(e

′

+ xke

= e

(1+ kx);

y2 = (xe

= x e

)

= e

y2′′ = (ekx )′(1+ kx)+ ekx (1+ kx)′ = kekx (1+ kx)+ ekxk = ekx (2k + k 2 x).

Подставив выражение для y , y′ и y′′ в исходное дифференциальное уравнение, получим

ekx (2k + k 2 x)+ pekx (1+ kx)+ qxekx = ekx (x(k 2 + pk + q)+ 2k + p)= 0.

Так как k является корнем характеристическогоуравнения k 2 + pk + q = 0 , то его корни находятся по формуле

− p ±

p2 − 4q

1,2

Если k

= k

, то p2 − 4q = 0, т.е. k = −

или 2k + p = 0.

Покажем, что решения

y = ekx

= xekx

являются линейно

независимыми. Для этого рассмотрим

ekx

= x ≠ const .

xekx

Таким образом, в этом случае общее решение уравнения имеет

вид

y = ekx (C

x).

+ C

Случай 3. Корни характеристического уравнения − комплекс-

ные числа:

− p ±

−

, где

p2 −

4q < 0.

1,2

= − p

(4q

− p

)= −

± i

4q − p

Тогда k

1,2

Обозначив

a =

− p

b =

4q − p

получим

k = a +bi

k2 = a −bi (b ≠ 0).

Частные решенияиможно записать в форме

y = e(a+ib) x ; y

= e(a−ib) x .

Это комплексные функции действительного аргумента,

удовлетворяющие дифференциальному уравнению y′′ + py′ + qy = 0 .

Проверим, что если комплексная функция действительного

аргумента

y = u(x) +iv(x)

удовлетворяет

рассматриваемому

дифференциальному уравнению, то этому уравнению удовлетворяют функции u(x) и v(x) . Подставляя выражение y = u(x) +iv(x) в

уравнение, будем иметь

(u(x) +iv(x))′′+ p(u(x) +iv(x))′+ q(u(x) +iv(x)) = 0 ,

или

(u′′+ pu′+ qu) +i(v′′+ pv′+ qv) ≡ 0.

Но комплексная функция равна нулю тогда и только тогда, когда равны нулю её действительная и мнимая части, т. е.

u′′+ pu′+ qu = 0 и v′′+ pv′+ qv = 0.

Это значит, что функции u(x) и v(x) являются решениями

уравнения.					= e(a+ib) x				= e(a−ib) x
Перепишем		функции y			= e(a+ib) x	; y		2	= e(a−ib) x	в	виде суммы
				1				2
действительной и мнимой частей:							= eax cosbx −ieax sin bx .
y	= eax cosbx +ieax sin bx ; y					2	= eax cosbx −ieax sin bx .
1						2
По доказанному выше следует, что действительные функции
y = eax cosbx	и	y	2	= eax sin bx	являются				решениями		уравнения.
1			2

Убедимся, что они будут линейно независимыми. Для этого рассмотрим

eax cosbx

= ctgx ≠ const.

eax sin bx

Таким образом, общее решение уравнения в случае

комплексных корней характеристического уравнения имеет вид

eax

Иsin bx , или

y = C eax cos bx + C

y = eax (C cos bx + C

sin bx).

Пример 1. Найти частное решение уравнения y′′+ 7 y′+12y = 0,

′

удовлетворяющее начальным условиям: y(0)=1; y (0)= −2.

Решение. Состав м характеристическое уравнение, заменив y′′,

y′,

y на k 2 ,

k , 1 соответственноб, получим k2 +7k +12 = 0 .

формуле

Корни

квадратного

уравнения

найдем

по

= −7 ± 7

− 4 12 = −7 ±

= −7 ±1 , откуда k

= −3 и k

= −4 .

1,2

ПодставляяСнайденные значения k1 и k2 в формулу для первого

случая, получим общее решение y

= C e−3x + C

e−4x .

Дифференцируя общее решение, получим

y′ = C1e−3x (−3)+ C2e−4x (− 4)= −3C1e−3x − 4C2e−4x .

Согласно заданным начальным условиям имеем

−3 0

+C2e

−4 0

;

1 = C1 +C2 ;

1 = C1e

или

−

e−4 0

или

−2 = −3C e−3 0

−2 = −3C1 −4C2 ,

=1−C ;

2 = C ,

откуда

−2 = −3C −4(1−C ), или

C1 = 2

C2 = −1.

Таким образом, искомым частным решением

является функция y = 2e−3x − e−4x .

7 y′′− y′−6y = 0.

Пример 2. Найти решение уравнения

Решение. Составим характеристическое уравнение,

заменив y′′,

y′, y на k 2 ,

k , 1 соответственно, получим 7k2 −k −6 = 0 .

= 1±

= 1±13 ,

Корни найдем по формуле

1+ 4 6 7

откуда

1,2

k =1 и

= − 6 . Подставляя найденные значения k и

в формулу,

И2

получим общее решение

y = С ex

+С

e−7 x .

Пример 3. Найти решение уравнения y′′+ 4y′+ 4y = 0.

′′

Решение. Составим характеристическое уравнение, заменив y

y′, y на k ,

4k + 4 =

0 .

k , 1 соответственно, получим k

Корни

найдем

по

−4 ±

16 −4 4

−4 ±0

= −2 ,

′′

формуле

kД=

1,2

k1 = k2 = −2 .

откуда

Подставляя найденные значения

в формулу,

получим общее решен е y = e−2x (C +C

x).

Пример 4. Найти решен е уравнения y

+ 9y = 0.

Решение.

оставим характеристическое уравнение k 2 +9 = 0 и

решим его:

k 2 = −9;

= ±

= ±3 i.

Уравнение

имеет

−9

9 (−1)

1,2

k1,2

= ±3i

(a = 0;

b = 3).

комплексные корни

По формуле общим решением будет

y = e0x (С cos

3x +С

sin 3x),

или y = С1 cos3x +С2 sin 3x.

Пример 5. Найти частное решение уравнения y′′ − 6y′ +10y = 0, удовлетворяющее начальным условиям: y(0)=1; y′(0)= 3.

Решение. Составим характеристическое уравнение k 2 −6k +10 = 0.

Корни найдем по формуле

	6 ±			= 6 ±		= 6 ± 2i = 3 ±i. (a = 3; b = 3).
		36 − 4 10
k =					− 4

1,2		2	2		2

По формуле общим решением будет функция

y = e3x (С1 cos x +С2 sin x).

Дифференцируя общее решение, получим

y′ = 3e3x (C1 cos x +C2 sin x)+ e3x (−C1 sin x +C2 cos x).

′

3, получим систе-

Подставив начальные условия y(0) = 1; y

(0)=

му для определения C1

и C2:

1 = e0 (C

cos 0 + C

sin 0),.

(C1 cos 0 + C2 sin 0)+ e

(−C1 sin 0 + C2 cos 0),

= 3 e

или

0),.

1 =1 (C

1+ C

0)+1(−C

1),

3 = 3 1(C

1+ C

0 + C

или

1 = C1;

C1 =1.

3 = 3C1 + C2 ; C2 = 0.

C1 =1;

C2 = 0 в

Подставив

полученные значения

констант

общее решение, получим y = e3x cos x

– искомое частное решение.

Задачи длябсамостоятельного решения

Найти решения

дифференциальных уравнений. В тех задачах, в

которых

заданы

начальные

условия,

найти

решения,

удовлетворяющие этим условиям.

y′′+ y′−2y = 0.

y′′+3y′ = 0.

y′′−4y′+5y = 0.

25y′′+ 4y = 0.

y′′− 2y′+ y = 0 при

y′′+ 2y′+ 2y = 0 при

y (0)= 4; y′(0)= −3.

y(0)= 0; y′(0)= −1.

y′′−8y′+15y = 0 при

y′′− 2y′+ 5y = 0 при

y (0)= 2; y′(0)=8.

y (0)=1; y′(0)= 3.

y′′+16y = 0 при

10.

y′′− 6y′+ 9y = 0 при

y (0)=1; y′(0)= 4.

y(0)= 2; y′(0)= 7.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1613 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20211.81 Mб431787.pdf
#
07.01.20211.82 Mб11788.pdf
#
07.01.20211.82 Mб51789.pdf
#
07.01.2021329.44 Кб4179.pdf
#
07.01.20211.82 Mб171790.pdf
#
07.01.20211.83 Mб81791.pdf
#
07.01.20211.83 Mб31792.pdf
#
07.01.20211.83 Mб71793.pdf
#
07.01.20211.83 Mб21794.pdf
#
07.01.20211.83 Mб21795.pdf
#
07.01.20211.83 Mб21796.pdf

Например, непосредственной подстановкой можно убедиться,

что функции

(C =1); y =3/ x

(C = 3) являются решениями

уравнения y

каждому дифференциальному уравнению