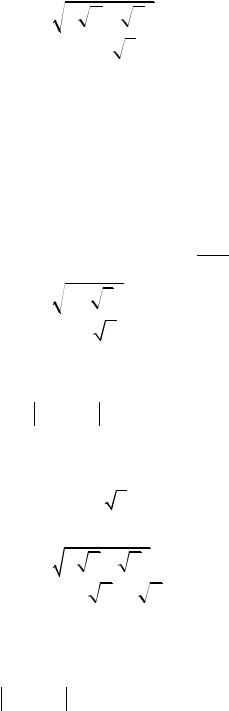
Контрольная работа по теме «Комплексные числа»
Вариант 1
1.Выполнить действия 7 −5i +i(1−i).
1−2i
2.Вычислить корень 3
−
2 −
6 i .
3.Решить уравнение z4 −1+ 
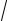3 i = 0.
4.Определить и построить множество точек, удовлетворяющих данным неравенствам:
а) Re z ≥ −2; б) −π ≤ arg z ≤ π .
2.Вычислить корень 4
1+А
3 i . ДИ
3.Решить уравнениебz3 −i
3 −3 = 0.
4.Определить и построить множество точек, удовлетворяющих данным уравнениямили неравенствам:С
|
1+ |
|
|
i 4 |
|
7 |
1. Выполнить действия |
|
|
|
|
|
. |
|
|
2 |
|
|
|
|
|
|
|
|
2.Вычислить корень 3
−
2 −
6 i .
3.Решить уравнение z4 −
2 +i
2 = 0.
4.Определить и построить множество точек, удовлетворяющих данным неравенствам:
а) Re z ≥ −2; б) z + 2 +i ≥ 2.
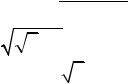
Вариант 4
1.Выполнить действия i15 + 6(2i +−1i)2 .
2.Вычислить корень 3
3 −i .
3.Решить уравнение z4 −1+ 
3 i = 0.
4.Определить и построить множество точек, удовлетворяющих данным уравнениям или неравенствам:
а) arg z = −π4 ; б) Im z > 3.
1. |
Владимирский, Б.М. Математика. Общий курс : учебник / Б.М. Вла- |
димирский, А.Б. Горстко, Я.М. Ерусалимский. − 2И-е изд., испр. и доп. – СПб. : |
Лань, 2004. – 960 с. |
|
|
|
2. |
Высшая математика в упражнениях и задачах: в 2 ч. : учебное пособие/ |
|
|
|
|
|
Д |
П.Е. Данко [и др.]. – 7-е изд., испр. – М. : ОНИКС : Мир и Образование, 2008. – |
Ч. 2. – 448 с. |
|
|
|
|
3. |
Пискунов, Н.С. ДифференциальноеАи интегральное исчисления: в 2 т. : |
учебное |
|
|
|
б |
|
4. |
Шипачев, В. . |
|
|
Курс высшей математики : учебник/ В.С. Шипачев ; ред. |
А. А. Тихонов. – 2-е изд., перераб. и доп. – М. : Проспект, 2005. – 600 с. |
5. |
|
и |
|
Матвеева, .В. Курс высшей математики : учебное пособие / С.В. Мат- |
6. |
Руппель, Е.Ю. Курс высшей математики : учебное пособие / Е.Ю. Руп- |
|
|
С |
|
|
пель. – Омск : СибАДИ, 2001. – Ч. 2. − 228 с. |
7. |
Задачник-практикум по математике: в 2 ч. : учебное пособие / Т.Е. Бол- |
довская, С.В. Матвеева, Е.Ю. Руппель. −Омск : СибАДИ, 2013.– Ч. 1. – 115 с.
8.Задачник-практикум по математике: в 2 ч. : учебное пособие / Е.Ю. Руппель, С.В. Матвеева, Т.Е. Болдовская. − Омск : СибАДИ, 2013. – Ч. 2. – 154 с.
9.Карасева, Р. Б. Математика [Электронный ресурс] : практикум для студентов технических направлений заочной формы обучения / Р. Б. Карасева,
С. В. Матвеева, Е. Ю. Руппель.− Электрон. дан. − Омск : СибАДИ, 2016. −
Режим доступа: http://bek.sibadi.org/fulltext/esd94.pdf, свободный.− Загл. с экрана
(дата обращения к ресурсу: 25.08.2016).
