
1753
.pdf
А А |
А |
А |
F |
|
1 |
|
F |
|
F |
|
1 |
. |
(5.18) |
|
|
||||||||||||
11 |
12 |
22 |
1 |
2 |
11 |
1 |
12 |
2 |
2 |
22 |
|
||
С другой стороны, учитывая то, что работа сил не зависит от порядка их приложения, можно записать
А F |
|
11 |
F |
|
|
F |
|
22 |
. |
(5.19) |
|
|
|
||||||||
1 |
2 |
2 |
|
21 |
2 |
2 |
|
|
||
Приравнивая два последних выражения, после преобразований получаются следующие равенства:
F1 12 F2 21 |
или |
A12 A21. |
(5.20) |
На основании полученных равенств формулируется теорема о взаимности работ (теорема Бетти): возможная работа внешних сил первого состояния на перемещениях по их направлениям, вызванных внешними силами второго состояния, равна возможной работе сил второго состояния на перемещениях по их направлениям, вызванных силами первого состояния.
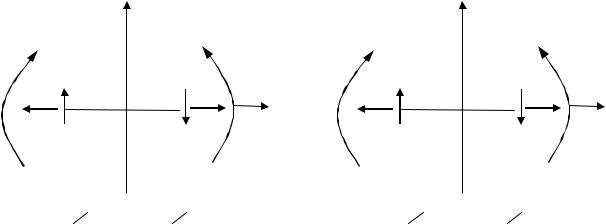
Снова рассмотрим два состояния системы. Но в качестве нагрузок в обоих состояниях примем силы F1 1 и F2 1. Тогда вызванные ими перемещения (рис. 5.10) будут единичными .
На основании теоремы Бетти можно записать F1 12 F2 21. По-
скольку силы F1 1 и F2 1, то следует равенство 12 21, называемое теоремой о взаимности перемещений (теорема Рэлея). Перемеще-
ния по направлению сил первого состояния от сил, равных единице, второго состояния равны перемещениям по направлению сил второго
состояния от сил, равных единице, первого состояния. |
|
|||
1-е состояние |
|
2-е состояние |
||
a _ |
b |
a |
_ |
b |
F1=1 |
|
|
F2=1 |
|
|
|
|
|
|
δ11 |
δ21 |
δ12 |
|
δ22 |
|
|
Рис. 5.10 |
|
|
5.6. Возможная работа внутренних сил
70
Определим возможную работу внутренних сил N, M и Q одного состояния на перемещениях, вызванных внутренними силами другого состояния (рис. 5.11).
В состоянии m под воздействием внешних сил в поперечном сечении рассматриваемого стержня возникают внутренние силы Nm, Mm и Qm. После возникновения усилий состояния m к рассматриваемому стержню прикладывают внешнюю нагрузку состояния n, которая вызывает появление в этом же поперечном сечении внутренних сил Nn, Mn и Qn.
y |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qm |
|
|
|
Qm |
x |
|
Qn |
|
|
|
Qn |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nm |
|
|
Nm |
Nn |
|
|
|
Nn |
|||||
Mm |
|
|
Mm |
Mn |
|
|
|
Mn |
|||||
|
|
|
ds |
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Состояние |
m |
|
|
Состояние n |
||||||||
|
|
|
|
|
|
Рис. 5.11 |
|
|
|
|
|
||
Рассмотрим возможную работу сил Nm, Mm и Qm на перемещениях, вызванных силами Nn, Mn и Qn. Поскольку определяется работа внутренних сил, то она будет со знаком минус.
Элементарная возможная работа, создаваемая внутренними силовыми факторами в соответствии с принципом суперпозиции, представляет собой сумму dWNm dWMm dWQm элементарных воз-
можных работ. Каждое из слагаемых этой суммы представляет собой произведение величин внутреннего силового фактора состояния m на соответствующее перемещение, вызванное силами состояния n, что
можно |
описать следующими |
выражениями:dW |
Nm |
N |
m |
|
Nnds |
; |
|||||||||||
EA |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Mnds |
|
|
|
|
Qnds |
|
|
|
|
|
|
||
dW |
M |
|
M |
m |
|
; dW |
Q |
m |
|
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||||||
|
m |
|
|
EJ |
Q |
|
|
GA |
|
|
|
|
|
|
|||||
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
71 |
|
|
|
|
|
|
|
|
|
|
|

Возможная работа внутренних сил для стержневой системы в целом описывается выражением
Wmn Nm |
|
Nnds |
Mm |
|
Mnds |
Qm |
Qnds |
. (5.21) |
EA |
EJ |
|
||||||
s |
|
s |
|
s |
GA |
|||
Аналогично выражению (5.21) можно записать возможную работу внутренних сил состояния n на перемещениях, вызванных действием внутренних сил состояния m:
Wnm Nn |
|
Nmds |
Mn |
|
Mmds |
Qn |
Qmds |
. (5.22) |
EA |
EJ |
|
||||||
s |
|
s |
|
s |
GA |
|||
Поскольку значения приведённых интегралов не зависят от перестановки местами значений внутренних усилий Nm, Mm, Qm и Nn, Mn, Qn, справедливым становится равенство Wmn Wnm , называемое в строительной механике теоремой о взаимности возможных работ внутренних усилий. Возможная работа внутренних сил состояния «m» на перемещениях, вызванных действием внутренних сил состояния «n», равна возможной работе внутренних сил состояния «n» на перемещениях, вызванных действием внутренних сил состояния «m».
5.7. Определение перемещений. Интеграл Мора
Рассмотрим теперь два состояния системы, показанные на рис. 5.12. В первом из них на систему действует произвольный комплекс внешних нагрузок, во втором только единичный силовой фак-
тор – сила Fk 1.
|
|
Состояние |
m |
|
Состояние k |
||||||
|
F |
|
|
q |
|
|
_ |
||||
|
|
М |
|
|
F2=1 |
||||||
2 |
|
|
|
|
|
2 |
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21
Рис.5.12
72

Составим выражение возможной работы, совершаемой заданным комплексом внешних и внутренних сил состояния k на перемещениях состояния m. Согласно принципу возможных перемещений, должно удовлетворяться равенство
Wkm Fk km 0. |
(5.23) |
При этом возможная работа внутренних сил состояния k на перемещениях состояния m
Wkm |
|
|
Nmd |
|
|
|
Mmd |
|
|
|
Qmd |
. (5.24) |
|
N |
k |
M |
k |
Qk |
|||||||||
EA |
EJ |
|
|||||||||||
s |
s |
s |
GA |
||||||||||
Возможная работа внешних сил состояния k на перемещениях состояния m будет равна
Fk km 1 km. |
(5.25) |
Подставляя в выражение (5.23) выражения (5.24) и (5.25), после арифметических преобразований получим
km |
|
|
Nmds |
|
|
|
Mmds |
|
|
|
Qmds |
. (5.26) |
|
N |
k |
M |
m |
Qk |
|||||||||
EA |
EJ |
|
|||||||||||
s |
s |
s |
GA |
||||||||||
Черта над обозначениями усилий означает, что эти усилия найдены от действия единичного силового фактора. Таким образом, перемещения от любой нагрузки можно выразить через внутренние усилия, возникающие в этой системе от действия на неё заданной внешней нагрузки и от действия на неё единичного силового фактора. При этом направление единичного силового фактора совпадает с направлением искомого перемещения.
Если определяется линейное перемещение (рис. 5.13), то в единичном (дополнительном) состоянии к системе, в той точке, перемещение которой определяется, прикладывается сила F 1. Если определяется угловое перемещение (рис. 5.14), то к тому сечению, угол поворота которого определяется, прикладывают сосредоточенный момент М 1.
_ |
73 |
|
_ |
|||
F =1 |
|
|
|
М=1 |
||
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.13 |
Рис. 5.14 |

Если определяют взаимное линейное смещение (рис. 5.15) двух точек системы, то в единичном состоянии к этим точкам по линии искомого смещения прикладывают единичные сосредоточенные силы, вектор которых направлен в разные стороны.
F=1 |
|
М=1 М=1 |
|
||
|
|
|
F=1 
Рис. 5.15 |
Рис. 5.16 |
Если определяют взаимное угловое перемещение двух сечений, то в единичном состоянии к этим двум сечениям (рис. 5.16) прикладывают сосредоточенные единичные моменты, вектор которых направлен в сторону возможного взаимного углового перемещения.
В общем виде формула для определения перемещений принимает вид выражения (5.26), называемого интегралом Мора.
Порядок определения перемещений:
находят аналитические выражения для определения внутренних усилий при действии на систему заданной внешней нагрузки (действительное состояние системы – состояние m);
по направлению искомого перемещения прикладывают соответствующий искомому перемещению единичный силовой фактор, от действия которого находят аналитическое выражение внутреннего силового фактора (единичное состояние системы – состояние k);
74

полученные аналитические выражения внутренних силовых факторов подставляют под знаки интегралов и осуществляют интегрирование, результатом которого является определение величины искомого перемещения.
При этом следует отметить, что если знак найденного перемещения окажется отрицательным, то это означает, что действительное направление искомого перемещения направлено в противоположную сторону действия единичного силового фактора.
5.8. Правило П. Верещагина
На практике часто встречаются случаи, когда на отдельных участках стержни имеют одинаковые физические и геометрические параметры, а одна из подынтегральных функций изменяется линейно. Тогда при учёте только, например, изгибающего момента соответствующее слагаемое интеграла Мора принимает следующий вид:
∆km |
1 |
|
|
k Mm ds. |
(5.27) |
|
M |
||||||
|
||||||
|
EJ s |
|
||||
Подынтегральные функции представляют собой функции, по которым строят соответствующие эпюры (рис. 5.17).
Принимая EJ 1 и переходя к интегрированию по координате х, получим
|
b |
|
||
km |
|
|
k Mm dx. |
(5.28) |
M |
||||
|
a |
|
||
На рис. 5.16 эпюра Mk представляет собой эпюру, построенную от того или иного силового фактора, равного единице (единичная эпюра), а эпюра Mm представляет собой эпюру, построенную от действия заданной внешней нагрузки. Такую эпюру называют грузовой эпюрой.
Из рис. 5.17 очевидно, что |
M |
k |
x a tg . Подставив это выра- |
|
жение под знак интеграла (5.28), получим |
|
|||
b |
|
|
||
km x a tg Mm dx tg x a d . |
(5.29) |
|||
c |
|
|
||
75

В выражении (5.27) d Mm dx дифференциал площади эпю-
ры Mm ; x a d статический момент площади эпюры Mm (пло-
щади ) относительно оси O O . Этот статический момент можно записать как Sm xс a , где (хс + а) расстояние от центра тяже-
сти эпюры Mm до оси O O . Таким образом, выражение (5.29)
b
можно переписать так: km Mk Mm dx xc a tg .
c
Произведение в правой части – хс а tg = yc.
O' |
|
|
|
|
|
|
Mк |
|
_ |
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
O |
α |
|
|
|
|
|
|
Эп. Мk |
|||
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
c |
|
x |
|
|
|
|
b |
||||
|
|
|
|
|
|
||||||
|
a |
|
|
|
|
|
|
||||
|
dΩ |
|
|
|
|
|
|
|
|
Эп. Мm |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
dx |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xс |
|
|
|
||||
_
Эпюра Мk единичного состояния.
Эпюра Мm действительного состояния (грузовая эпюра).
Рис.5.17
В выражении (5.27) d Mm dx дифференциал площади пюры
Mm ; x a d статический момент площади эпюры Mm (площа-
ди ) относительно оси O O . Этот статический момент можно записать как Sm xс a , где (хс + а) расстояние от центра тяже-
сти эпюры Mm до оси O O . Таким образом, выражение (5.29)
|
b |
Mm dx xc |
a tg . Про- |
||
можно переписать так: km |
|
M |
k |
||
|
c |
|
|
||
изведение в правой части – хс а tg = yc. На основании изложенного
b |
|
||
km |
|
k Mm dx ·yc. |
(5.30) |
M |
|||
a |
|
||
Окончательно можно записать следующее равенство:
76
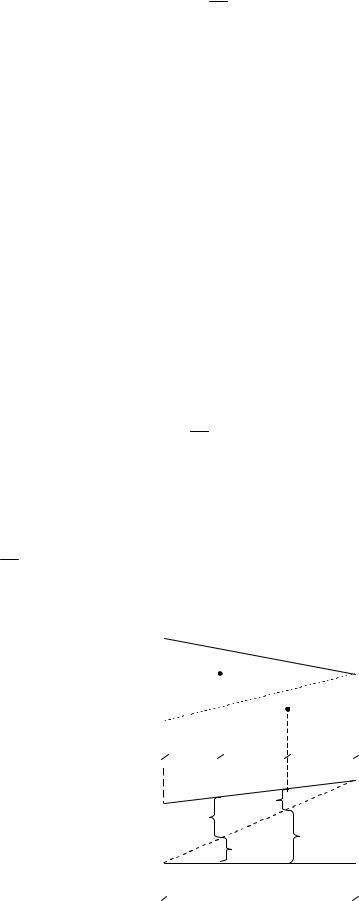
km |
1 |
|
|
k |
Mm |
ds |
yc |
|
Эп.Мk Эп.Мm |
. (5.31) |
|
M |
|||||||||||
|
|
|
|||||||||
|
EJ s |
|
|
EJ |
EJ |
||||||
Таким образом, доказана возможность интегрирования методом перемножения эпюр. Перемножить две эпюры найти площадь одной из них и умножить на ординату, снятую на другой и находящуюся под центром тяжести первой. Знак произведения считается положительным, если обе перемножаемые эпюры находятся по одну сторону стержня. Следует помнить, что если перемножаются две прямолинейные эпюры, то не имеет значения, на какой из них брать площадь, а на какой ординату. Если одна из перемножаемых эпюр является криволинейной, то необходимо брать площадь именно криволинейной эпюры. Перемножать эпюры можно только на тех участках, на которых обе эпюры являются неломаными и жёсткостные характеристики поперечных сечений являются постоянными. В противном случае перемножение эпюр необходимо осуществлять по участкам. Тогда выражение (5.31) примет вид
km |
1 |
|
|
k Mm ds |
Эп.Мk Эп.Мm |
. |
(5.32) |
|
M |
||||||||
|
|
|||||||
|
EJ s |
EJ |
|
|||||
Суммирование по выражению (5.32) должно осуществляться по всем участкам, по длине которых имеет место непрерывность подын-
тегральных функций Mk и Mm .
В качестве примера (рис. 5.18) покажем перемножение двух трапеций.
Для |
того чтобы удобно |
было |
|
I |
|
|
|
|
Эп. Мm |
|||||
а |
|
|
|
|
|
|
||||||||
находить |
центр |
тяжести |
эпюр, |
|
|
|
II |
|
b |
|||||
необходимо эти эпюры разделять |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||
на простые фигуры, положение |
|
ℓ/3 |
|
ℓ/3 |
ℓ/3 |
|
|
|||||||
центра тяжести которых извест- |
|
|
|
_ |
||||||||||
|
|
|
|
|
|
|
||||||||
но. В данном случае обе трапе- |
|
|
|
|
|
|
|
Эп. Мk |
||||||
|
|
|
|
|
|
|
||||||||
ции можно представить состоя- |
|
y1 |
|
y2 |
y2 |
' |
|
|
||||||
|
|
|
|
|||||||||||
щими |
из |
двух |
треугольников, |
c |
|
|
d |
|||||||
|
|
I |
|
|||||||||||
III |
|
|
|
|
||||||||||
обозначенных римскими цифра- |
|
|
y1' |
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||
ми. Тогда по формуле (5.31) |
|
|
|
ℓ |
|
|
|
|
||||||
km = I III + I IV + II III +II IV= |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
1 |
|
1 y1 1 |
y1 2 |
77 |
|
|
|
|
|
|
|
|
||
|
|
|
y2 |
|
|
Рис. 5.18 |
|
|
|
|
||||
EJ |
|
|
|
|
|
|
||||||||

|
|
|
|
1 |
1 |
2 |
1 |
1 |
|
1 |
1 |
1 |
2 |
|
|||||||||||
2 |
y |
|
|
|
|
a |
|
c |
|
|
a |
|
|
d |
|
b |
|
|
c |
|
|
b |
|
d |
|
2 ) |
3 |
2 |
3 |
3 |
|||||||||||||||||||||
|
|
|
|
EJ 2 |
3 |
|
2 |
|
|
|
|
2 |
|
|
|||||||||||
|
|
|
2 ac bd ad bc . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
6EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Полученное выражение носит название формулы трапеции.
5.9. Определение перемещений от действия температуры
Интеграл Мора, как отмечалось в предыдущем подразделе, может быть представлен в следующем виде:
km |
Mk |
Nk s |
Qn y . |
(5.33) |
||
|
s |
|
s |
s |
|
|
В выражении (5.33) |
|
Mmds |
взаимный угол поворота тор- |
|||
|
||||||
|
|
|
EJ |
|
|
|
цевых сечений (рис. 5.19) элемента, имеющего бесконечно малую
длину ds стержня от заданной внешней нагрузки; s |
Nm ds |
вза- |
||||
|
||||||
|
|
Qmds |
EA |
|||
имное смещение торцевых сечений ds; y |
|
взаимное |
||||
GA |
||||||
|
|
|
|
|||
смещение торцевых сечений вдоль оси, перпендикулярной оси элемента. В таком виде интеграл Мора может быть использован для определения перемещений не только от действия сил, но и от температуры.
Пусть верхнее волокно элемента ds нагрето на t1, а нижнее на t2. При этом t1 t2 . Распределение температуры по высоте сечения принято по прямолинейному закону. При температурном коэффициенте линейного расширения верхнее волокно удлинится на t1ds, а нижнее на t2ds. На уровне нейтральной оси это удлинение, что очевидно из рис. 5.19, составит полусумму удлинений верхнего и нижнего волокон элемента ds.
sm |
st |
|
t1 t2 |
ds. |
(5.34) |
|
|||||
|
|
2 |
|
|
|
|
|
78 |
|
|
|

Выражение (5.34) соответствует тому состоянию элемента ds, при котором он по всей высоте сечения h получил равномерное изменение температуры. От неравномерного нагрева торцевые сечения элемента ds поворачиваются на угол
m |
t |
|
t1 t2 |
ds. |
(5.35) |
|
|||||
|
|
|
h |
|
|
Деформация сдвига в элементе ds не возникает, т.е. уn 0.
Подставляя (5.34) и (5.35) в (5.33), получим интеграл Мора для определения температурных перемещений.
kt |
|
t1 t2 |
|
|
k |
ds |
t1 t2 |
|
|
k |
ds. |
(5.36) |
|||||
M |
N |
||||||||||||||||
h |
2 |
||||||||||||||||
|
|
|
|
|
s |
|
s |
|
|
||||||||
|
|
|
|
αt1ds |
|
|
|
|
ds |
αt1ds |
|
|
|||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
∆φt |
|
|
|
|
|
|
|
|
|
∆φt |
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
∆st |
|
|
|
|
|
∆st |
|
|
|
|
|
|
|
h |
2 |
|
|
|
|
|
2 |
|
|
|
|
z |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 ds
ds 
 αt2ds αt2ds 2 2
αt2ds αt2ds 2 2
Рис. 5.19
Интеграл Мора (5.34) значительно упрощается тогда, когда интегрирование ведётся для прямолинейных или ломаных стержней, имеющих по длине постоянное поперечное сечение. В этом случае интегралы могут быть определены, как площади единичных эпюр.
kt |
|
t1 t2 |
|
|
|
t1 t2 |
|
|
, |
(5.37) |
h |
M |
|
N |
|||||||
|
|
|
|
2 |
|
|
|
|
||
|
|
|
79 |
|
|
|
|
|
||
