
1634
.pdf
1. |
|
2 |
|
|
3 |
7 |
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2. xe |
|
dx. |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
2 |
|
x |
|
|
dx. |
|
|
|
|
|
|
|||||||||||||||||
|
x |
|
|
|
|
|
|
11 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
|
|
|
||||||||||||
3. |
|
tgx 2 |
dx. |
|
|
|
4. |
|
|
|
|
|
|
|
dx. |
||||||||||||||||
|
|
cos |
2 |
x |
|
|
|
|
|
4x x |
2 |
|
|
||||||||||||||||||
|
|
|
|
x 1 |
|
|
|
|
|
|
|
8 |
|||||||||||||||||||
5. |
|
|
|
|
|
|
|
|
|
|
|
dx. |
6. (3x2 |
8)cos4xdx. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
(x 1)(x 3)(x 7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
dx. |
|||||||||||||||||||||||
7. cos2 3x sin2 4xdx. |
8. |
|
|
2x 1 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x 1 |
||||||||
Вариант 13
|
2 |
|
|
5 |
|
|
|
3 |
|||
1. |
|
|
|
|
|
|
|
|
|
|
dx. |
|
2 |
4 x |
2 |
6 |
|
|
|
||||
|
|
|
|||||||||
1 x |
|
|
|
|
|
|
x |
||||
4tgx 1 3. cos2 x dx.
x 1
5. (x 5)(x2 7)dx.
7. sin x dx. cosx 1
Вариант 14
2. |
|
|
dx |
|
|
. |
|
|
|||
|
|
|
|
|
|
|
|||||
|
1 (8x)2 |
|
|||||||||
|
|
|
|
|
|
|
|
||||
4. |
|
|
4x |
|
|
|
|
dx. |
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
x2 x 2 |
|||||||
6. (2x 1)e4xdx. |
|||||||||||
8. |
|
|
|
xdx |
dx. |
||||||
|
|
|
|
|
|
||||||
|
|
x 1 2 |
|
|
|
|
|
||||
1. 2 3x2 5x 7ex dx.
3. (3log7 x 2)3 dx. x
7x2 1
5. (x2 x 1)(3x 1)dx. 7. sin3 xcos4 xdx.
2. 54x 1dx.
2x 1
4. x2 9x 2dx.
6. (4x 8)sin8xdx.
8. |
|
x |
2 |
dx. |
|
|
|
||
|
x 1 |
|||
|
|
|
|
|
|
Вариант 15 |
|
||
1. (3sin x |
|
2 |
|
|
|
3 |
|
)dx. |
2. 75x 11dx. |
|
|
|
|
|
|
||||
|
|
|
|||||||
|
1 x2 |
6 x2 |
|
||||||

3. |
(4arctgx 3) |
4 |
|
dx. |
||
1 x |
2 |
|
|
|||
|
|
|
|
|
|
|
5. |
|
x 1 |
|
|
dx. |
|
|
|
|
|
|
||
|
|
(x 8)(x 11) |
||||
7. sin3 4xcos3 4xdx.
Вариант 16
1. |
|
7 |
|
|
|
8 |
|
|
|
||
|
|
|
|
|
|
|
2x dx. |
||||
|
|
2 |
4 x |
2 |
|||||||
|
4 x |
|
|
|
|
|
|
||||
3. 2x3 |
x2dx. |
|
|
|
|||||||
5. |
|
|
|
|
2x 1 |
|
|
dx. |
|||
|
(x 1)(x |
2 |
|
|
|
||||||
|
|
|
3x 5) |
||||||||
7. sin5xcos5xsin10xdx.
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 17 |
|
1. |
|
3cosx 7sinx 26 |
|
|
1 |
|
|||||||
|
|
||||||||||||
|
x |
|
dx. |
||||||||||
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
||
3. |
|
e |
x |
dx |
|
|
|
|
|
||||
|
|
|
|
|
|
. |
|
|
|
|
|
||
|
|
|
x |
2 |
|
|
|
|
|
||||
|
|
|
|
x 8 |
|
|
|
|
|
||||
5. |
|
|
|
|
|
dx. |
|
|
|
|
|||
|
(x 3)(x 5) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||
7. sin5 3xdx.
Вариант 18
|
|
x |
|
7 |
|
|
8 |
|
|
|
|
3 7 |
x |
|
|
|
|
|
|||
|
|
3 |
|
|
|
|||||
1. |
|
|
x |
2 |
|
dx. |
||||
|
|
|
|
|
|
|
|
|
|
4. |
|
|
x 1 |
|
dx. |
|
|
|
|
||
x |
2 |
||||
|
|
6x 8 |
|
|
6. (5x 8)cos3xdx.
8. 
 x 1 1dx.
x 1 1dx. 
 x 1 5
x 1 5
2. 38x 1dx. |
|
|
||||||
4. |
|
|
|
3x 1 |
|
dx. |
||
|
|
|
|
|
|
|||
|
|
x2 6x 8 |
||||||
|
|
|
|
|
|
|||
6. arcctg3xdx. |
|
|
||||||
8. |
|
|
|
x |
dx. |
|
|
|
|
|
|
|
|
|
|
||
|
|
x 1 |
|
|
||||
2. |
|
|
|
dx |
|
. |
cos |
2 |
|
||||
|
(6x 3) |
|||||
4. |
|
|
x 8 |
dx. |
||
x |
2 |
4x 6 |
||||
|
|
|
|
|||
6. arcsin8xdx.
dx
8. 
 x 3
x 3 x 24
x 24
 x dx.
x dx.
2. e8x 1dx.
3. xsin7x2dx. |
|
4. |
|
|
|
x 1 |
|
dx. |
|||
|
|
|
|
|
|
|
|
||||
|
|
|
x2 6x 6 |
||||||||
|
x 8 |
|
|
|
|
|
|
||||
5. |
dx. |
6. e3x x3dx. |
|
|
|||||||
(x 3)(x 3)(x 1) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7. sin4 3xcos3xdx. |
|
8. |
1 |
x |
dx. |
|
|
||||
|
1 |
|
|
|
|||||||
|
|
|
|
x |
|
|
|||||
Вариант 19
1. (2cosx 3x 4x 6x x6)dx.
exdx
3. 1 e2x .
x 8
5. (x2 5)(x 5)dx.
7. cos2xsin2 6xdx.
Вариант 20
2. cos(12 11x)dx.
4. |
|
x |
|
dx. |
|
|
|
|
|||
x2 10x |
|||||
|
|
|
|
6. (4x 1)23xdx.
8. |
|
x |
1 |
dx. |
|
|
|
||
|
x 1 1 |
|||
1. |
|
2 |
|
|
|
|
5 |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2. cos(8x 3)dx. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
5 x2 |
|
7 x |
dx. |
|
|
||||||||||||||||||||
|
|
|
|
|
4 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
|
3x |
|
|
|
|
|
|
|
|
|
4. |
|
|
|
3x 1 |
dx. |
||||||||||||||
|
|
|
|
|
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 10x 1 |
|||||||||||||||||||
|
|
|
|
|
|
|
7x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
5. |
|
|
|
|
|
|
|
|
dx. |
|
|
|
|
|
|
6. |
|
x3 log4 xdx. |
|
|||||||||||||
(x 1)(x 6) |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
7. |
|
|
|
|
|
cosx |
|
|
|
|
|
|
|
|
|
3x 1 |
dx |
|
||||||||||||||
|
dx. |
|
|
|
|
8. |
|
|
|
. |
|
|||||||||||||||||||||
sin x cosx |
|
|
|
|
|
|
|
|
|
4 |
|
|||||||||||||||||||||
|
|
|
|
3x 1 |
|
|||||||||||||||||||||||||||
|
3 |
|
|
6 |
|
|
|
7 |
|
||
1. |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
7 |
|
|
|
|||
|
|
x |
|
x |
|
||||||
x |
|
|
|
|
|
|
|
|
|||
3. 
 5lnxx 1dx.
5lnxx 1dx.
2 dx.
Вариант 21
2. |
dx |
. |
|
||
|
|
||||
|
4 x |
|
|||
4. |
|
|
|
x |
dx. |
x |
2 |
10x 2 |
|||
|
|
|
|||

3x2 1
5. (4 x)(x2 4)dx. 7. cos4 5xdx.
1. |
2 |
|
3 |
7 |
|
|
|
||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
7 |
x dx. |
||||
|
6 |
|
x |
2 |
|||||||||
|
x |
|
|
|
|
|
|
|
|
|
|||
3. |
|
3tgx 4 |
dx. |
|
|
|
|||||||
|
2 |
|
|
|
|||||||||
|
|
cos |
x |
|
|
|
|
|
|
||||
5. |
|
|
|
|
|
|
x2 |
|
|
dx. |
|||
|
(x |
2 |
|
|
|
|
|
|
|
||||
|
|
|
10)(x 1) |
||||||||||
7. sin5 3xdx.
1. |
|
2 |
|
|
|
|
|
1 x |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
7 |
|
||||
|
|
|
|
|
|
|
|
|
||||||||
3 |
|
x |
|
3 |
|
x |
1 dx. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
3. |
arcsin x |
|
dx. |
|
|
|||||||||||
|
|
|
|
|
||||||||||||
|
|
|
||||||||||||||
|
|
|
|
1 x2 |
|
|
|
|
||||||||
5. |
|
|
|
|
|
|
|
|
|
x2 |
11 |
|
dx. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
(x 1)(x 1)(x 2) |
|||||||||||||
7. sin2 4x cos3xdx.
1. (3cosx 6x 8x10)dx.
3. sin x5 5cos 1dx.
5cos 1dx.
5. |
2x 1 |
|
dx. |
||
|
|
|
|
||
|
(x 1)(x 8) |
||||
7. |
sin х |
|
|
dx. |
|
3 |
х |
||||
|
1 cos |
|
|
||
6. (x3 1)ln xdx.
dx
8. 4
 x 1
x 1 
 x 1.
x 1.
Вариант 22
2. |
|
|
|
|
dx |
. |
|
|
||||
cos |
2 |
|
|
|
||||||||
|
|
(7x 3) |
|
|
|
|||||||
4. |
|
|
|
|
x 2 |
|
|
dx. |
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x2 12x 8 |
||||||||
6. (4x 1)cosxdx. |
||||||||||||
8. |
|
|
|
|
dx |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
3 |
x 4 x |
|
|
|
||||||||
Вариант 23
2. |
|
|
|
|
|
dx |
. |
||
|
sin |
2 |
|
||||||
|
|
(6x 1) |
|
|
|||||
4. |
|
|
|
|
|
x 8 |
|
dx. |
|
|
x |
2 |
|
|
|
|
|||
|
|
|
6x 20 |
||||||
6. (x 8)e3xdx. |
|||||||||
|
3 |
|
1 |
dx. |
|
|
|||
8. |
x |
|
|
||||||
|
|
|
|
|
|
|
|||
|
|
|
|
x 1 |
|
|
|||
Вариант 24
2. |
dx |
. |
|
|
|
|
|
|
|
||
|
4 3x |
|
|
||
4. |
|
|
2x |
|
dx. |
|
|
|
|
||
|
x2 4x 20 |
||||
|
|
|
|
||
6. (7x 8)cos11xdx.
|
|
dx |
|||
8. |
|
|
|
|
. |
1 |
|
|
|
||
|
5x 4 |
||||

Вариант 25
1. (3sin x 2ex e 3x 11)dx.
3. x3ex4dx.
x
5. (x 1)(x 10)dx.
7. sin xcosxsin6xdx.
Вариант 26
2. |
dx |
|
. |
6 (8x) |
2 |
||
|
|
|
|
4. |
3x 6 |
dx. |
|
2 |
|||
|
x 8x |
|
|
6. (5x 11)e3xdx.
x
8. 
 3x 1 2dx.
3x 1 2dx.
1. (x3x 7 3x 3 7x cosx)dx.
dx
3. x3 2ln x 4.
2ln x 4.
x
5. (x 8)(x 8)(x 3)dx. 7. sin2 2xdx.
Вариант 27
2. |
|
|
dx |
|
. |
|
|||
1 (3x) |
2 |
||||||||
|
|
|
|
|
|
||||
4. |
|
|
3x 8 |
dx. |
|||||
x |
2 |
|
|
||||||
|
|
6x 1 |
|||||||
6. xcos2 xdx. |
|||||||||
8. |
|
|
|
dx |
|
. |
|||
|
|
|
|
|
|||||
3 |
x 1 1 |
||||||||
1. |
( |
3 |
|
|
|
6 |
|
|
2 |
2x)dx. |
2. sin(11x 8)dx. |
|
|
|||||||||||
2 |
x |
|
2 |
|
|
|
|
|||||||||||||||||
|
|
|
sin |
|
cos |
x x |
|
|
|
|
|
|
|
x |
|
|
||||||||
3. x3 cos(2x4 |
1)dx. |
4. |
|
|
|
|
|
|
|
dx. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
7 x2 2x |
||||||||||||||||||||||
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
5. |
|
|
|
dx. |
6. arctg |
|
|
|
|
|
||||||||||||||
|
|
|
xdx. |
|
|
|||||||||||||||||||
|
(x 8)(x 2) |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
1 |
dx. |
|
|
||||||||||||||
7. sin2 3xcos2 3xdx. |
8. |
|
|
x |
|
|
||||||||||||||||||
3 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
||||||
Вариант 28
1. ( |
3 |
|
|
6 |
|
|
7 |
|
)dx. |
|
|
2 |
|
2 |
|
|
|
||||
1 x |
1 x |
6 |
||||||||
|
|
|
|
|
|
x |
||||
3. cosx
 sin xdx.
sin xdx.
2. 26x 2dx.
4. |
|
2x 4 |
|
dx. |
|
|
|
||
|
||||
|
|
3 x2 6x |
||

5. |
|
|
|
|
|
x 3 |
|
|
dx. |
|
6. (7x 1)cosxdx. |
||||||||||||
|
(2 x)(x 4)(x 1) |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||
7. cos35xdx. |
|
|
|
|
|
|
8. |
|
|
x |
dx. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
x 1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
x |
|
|
|
16 |
|
|
|
|
|
|
|
3x 1 |
|
|
||||
1. |
( |
3 |
7cosx |
|
|
x |
3 |
)dx. |
2. e |
|
|
||||||||||||
|
|
|
|
|
|
|
|
dx. |
|||||||||||||||
x |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7x 1 |
|
|||||
3. sin x(3cosx 1)4dx. |
|
|
4. |
|
|
dx. |
|||||||||||||||||
|
|
x |
2 |
||||||||||||||||||||
|
|
|
|
7x 2 |
|
|
|
|
|
|
|
|
|
|
x 5 |
||||||||
5. |
|
|
|
dx. |
|
|
|
|
|
|
6. x2e xdx. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
(x 1)(x 8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7. sin8xcos3xdx. |
|
|
|
|
|
|
8. |
|
|
|
|
x |
|
dx. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
x 1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вариант 30
3
1. (3sin x 2cosx x23 x)dx. 3. x2 sin(3x3 4)dx.
x)dx. 3. x2 sin(3x3 4)dx.
x
5. (x 1)(x 11)dx.
7. sin6xcos2 xdx.
2. cos(3x 2)dx.
3x 1
4. x2 20x 2dx.
6. x 3xdx.
dx
8. 
 x 3
x 3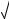 x .
x .
Раздел 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§1. Задача о площади криволинейной трапеции
|
y f (x) |
|
T |
a |
b |
|
Рис. 1 |
|
Решение. |
a x0 x1 x2 |
|
k 1,2,...,n. |
|
Пусть задана непрерывная функция y f (x) 0 на отрезке a,b . Задача: найти площадь криволинейной трапеции ST , то есть площадь плоской фигуры T , ограниченной кривой y f (x), прямыми y 0; x a; x b (рис. 1).
Разобьем |
отрезок |
a,b произвольно точками |
... xk 1 xk |
... xn b. |
Обозначим xk xk xk 1, |
f (~xk )






































 f (~x1)
f (~x1) 













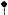


|
a x |
~ |
~ |
|
x |
~ |
x |
x |
~ |
|
|
|
|
x x |
x x |
2 |
x |
x |
|||||||
|
0 |
1 1 |
2 |
k 1 |
k |
k |
n 1 x b |
|
||||
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
Рис. 2 |
|
|
|
|
|
|
|
В каждом из получившихся отрезков xk 1,xk |
|
выберем произвольно |
||||||||||
~ |
и вычислим значение функции |
y f |
~ |
|
в выбранных точках. |
|||||||
точки xk |
(xk ) |
|||||||||||
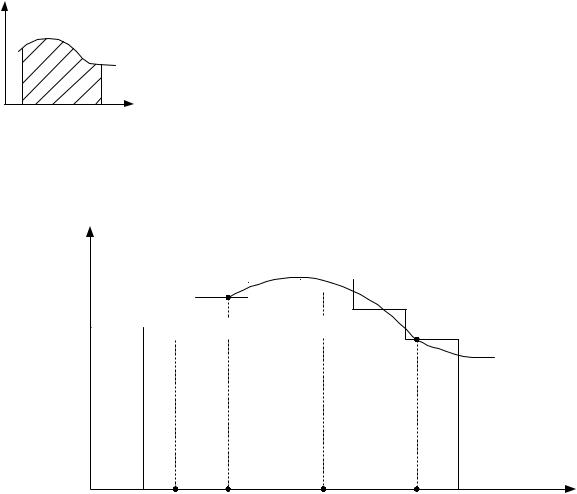
Составим ступенчатую фигуру из прямоугольников, основаниями которых
служат отрезки xk 1,xk , а высоты равны |
~ |
|
|
|
f (xk ) (рис. 2). |
|
|||
Площадь ступенчатой фигуры равна |
|
n |
|
|
~ |
~ |
~ |
~ |
|
Sn f (x1) x1 |
f (x2) x2 ... f (xn) xn |
f (xk ) xk . |
||
k 1
Получили Sn – последовательность сумм.
Можно считать, что площадь ступенчатой фигуры примерно равна площади криволинейной трапеции:
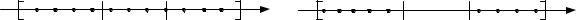
ST Sn .
Ошибка вычисления будет тем меньше, чем больше точек выбирается на a,b . Положим по определению
ST nlim Sn .
Замечание. Предел вычисляем при условии, что одновременно с увеличением числа n выполняется условие xk 0, то есть при увеличении числа точек xk нужно следить за тем, чтобы все длины отрезков xk 1,xk стремились к нулю.
a x0 |
x1 |
x2 |
b xn |
a x0 |
x1 |
x2 |
b xn |
|
|
Рис. 3 |
|
|
|
Рис. 4 |
|
На рис. 3 показано правильное расположение точек на a,b , на рис. 4
– неправильное, т.к. x1,x2 при увеличении числа точек не изменяет своей длины.
§2.Определение определенного интеграла и его геометрический смысл
Пусть функция y f (x) определена на отрезке a,b . Аналогично тому, как это сделано в предыдущем параграфе, составим сумму
n
f (~xk ) xk . Будем называть её интегральной суммой.
k 1
О п р е д е л е н и е . Определённым интегралом от функции y f (x) на a,b называется число, равное пределу
lim |
n |
~ |
f (xk ) xk . |
||
n |
k 1 |
|
xk 0 |
b |
|
|
f (x)dx или f (x)dx. При этом b |
|
Это число обозначается символом |
||
|
a |
a,b |
– верхний предел, a – нижний предел интегрирования. Итак,
b |
lim |
n |
~ |
f (x)dx |
f (xk ) xk . |
||
a |
n |
k 1 |
|
|
xk 0 |
|
|
|
|
|
|
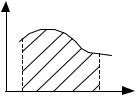
Геометрический смысл |
|
y |
|
|
|
b |
|
|
|
|
|
|
|
|
|
y f (x) |
Если f (x) 0 на a,b , то f (x)dx равен пло- |
||
|
|
T |
|
a |
|
0 |
|
|
|
щади криволинейной трапеции ST |
(рис. 5). |
a |
b |
x |
|
|
|
|
|
Рис. 5 |
|
|
|
Свойства определенного интеграла
a
1. f (x)dx 0.
a
ba
2.f (x)dx f (x)dx.
ab
Эти свойства очевидно следуют из определения определенного интеграла.
b |
|
b |
|
b |
|
|
|
|
|
|
|
|
|
3. f (x) g(x)dx f (x)dx g(x)dx. |
|
|
|
|
|
|
|
||||||
a |
|
a |
|
a |
|
|
|
|
|
|
|
|
|
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
n |
~ |
|
~ |
|
|
|
|
|
|
f (x) g(x)dx lim |
f |
(xk ) g(xk ) xk |
|
|
||||||||
|
a |
|
|
n k 1 |
|
|
|
|
|
|
|
||
|
|
|
n |
~ |
|
|
n |
~ |
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
||
|
lim |
(xk ) xk |
g(xk ) xk |
|
|
|
|||||||
|
n |
k 1 |
|
|
k 1 |
|
|
|
|
|
|
||
|
n |
~ |
|
n |
|
~ |
|
b |
|
|
b |
|
|
lim f (xk ) xk lim g(xk ) xk f (x)dx g(x)dx. |
|||||||||||||
n k 1 |
|
|
n k 1 |
|
|
|
a |
|
|
a |
|
|
|
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
4. c f (x)dx c f (x)dx. |
|
|
|
|
|
|
|
|
|
|
|||
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
n |
~ |
|
|
|
|
n |
~ |
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
||
f (x)dx lim c f (xk ) xk lim c |
f (xk ) xk |
||||||||||||
a |
|
n k 1 |
|
|
|
n k 1 |
|
|
|
|
|||
|
n |
~ |
b |
|
|
|
|
|
|
|
|
|
|
c lim f (xk ) xk c f (x)dx. |
|
|
|
|
|
|
|||||||
|
n k 1 |
|
a |
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
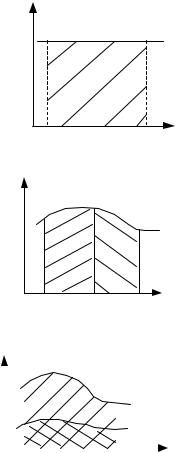
5. c dx c(b a). |
|
|
|
y c |
|
||
a |
|
|
|
|
c |
|
|
|
|
|
|
|
|
||
Доказательство. Это свойство очевидно |
|
|
|
||||
из рис. 6. |
|
|
|
|
|
|
|
6. Если a c b, то |
|
|
|
|
|
||
b |
|
c |
b |
|
|
|
|
f (x)dx f (x)dx f (x)dx. |
a |
|
b |
||||
a |
|
a |
c |
|
|
Рис. 6 |
|
Свойство проиллюстрировано на рис. 7. |
|
|
|
||||
|
|
|
b |
|
|
y f(x) |
|
7. Если |
f (x) 0 |
на a,b , то |
f (x)dx 0. |
|
|||
|
|
|
a |
|
|
|
|
8. Если |
f (x) 0 |
на a,b , то |
|
|
|
|
|
|
b |
f (x)dx 0. |
|
|
|
|
|
|
|
|
a |
c |
b |
||
|
a |
|
|
|
|||
|
|
|
|
|
|
|
|
9. Если |
f (x) g(x) |
на a,b , то |
|
|
|
|
|
|
|
Рис. 7 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f (x)dx g(x)dx (рис. 8). |
|
|
|
|
|
|
|
|
|
|
y=g(x) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y =f(x) |
|||||||
|
b |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
10. |
f (x)dx |
|
|
f (x) |
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
a |
|
b |
||||||||||||||||||||||||
|
a |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Доказательство. Очевидно, что |
|
f (x) |
|
f (x) |
|
f (x) |
|
. |
Рис. 8 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Проинтегрируем по отрезку a,b . |
|
По |
|
свойству 9 |
|
получаем |
||||||||||||||||||||||
|
b |
|
|
|
|
b |
|
b |
|
|
b |
|
|
|
|
|
|
b |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
f (x) |
dx |
f (x)dx |
f (x) |
dx, то есть |
|
|
|
f (x)dx |
|
f (x) |
dx. |
|||||||||||||||
|
a |
|
|
|
|
a |
|
a |
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
||||||
Следствия:
1. Если на a,b верно, что |
f (x) k, то |
b |
f (x)dx |
k(b a). |
|
||||
|
|
a |
|
|
2. Если m наименьшее, |
M наибольшее значения функции |
y f (x) |
b |
|
|
на a,b , то m(b a) f (x)dx M(b a). |
|
|
a |
|
|
11. Теорема о среднем значении. |
|
|
Пусть функция y f (x) |
непрерывна на a,b . Тогда существует точка |
|
b
c a,b ,такая, что |
f (x)dx f (c) (b a). |
a |
|
