Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1634

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.45 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 153 4 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

excosxdx

u ex du exdx;

sinx ex

exsinxdx

dv cosdx v cosxdx sinx.

u ex du exdx;

sinx ex

ex cosx cosx exdx

dv sinxdx v cosx.

sin x ex ex cosx ex cosxdx.

Запишем результат наших вычислений:

I ex(sinx cosx) I.

Выразим отсюда I как из уравнения:

cosxdx

(sin x cosx) C.

x2 a2

dx;

a2 dx

x2 a

12.I

2 x

dv dx v dx x.

dx x

(x2

a2)

dx x

x2 a2

I a2 ln

x2 a2

dx a2

x2 a2

Этот интеграл также является круговым. Получаем

I x

x2 a2

a2 ln

x2 a2

x x

lnx

u lnx du

;

13.

(1 x)2

dx v (1 x) 2d(1 x)

(1 x)2

1 x

lnx

1 x

1 x x

x 1

ln x

x 1

1 x

;

xarctg

u arctg

14. arctg

xdx

1 x 2 x

dv dx v dx x.

заменаt

;

2tdt

(t2 1) 1

x t2;dx 2tdt.

xarctg

1 t2

xarctg

x 1

dt xarctg

x t arctgt C xarctg x

1 t2

arctg

C (x 1)arctg

15. (arcsin x)2dx

u (arcsin x)2 du

2arcsin x

dx;

xarcsin2 x

1 x2

dv dx v x

u arcsinx du

;

2xarcsin x

1 x2

2xdx

d(1 x2

)

1 x2

dx v

1 x2

xarcsin2 x 2 1 x2 arcsin x

1 x2

xarcsin

2 x

1 x

2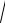1 x2 arcsin x 2 dx xarcsin2 x 2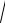1 x2 arcsin x 2x C.

Задачи для самостоятельного решения

Вычислить интегралы, используя формулу интегрирования по частям.

1. (3x 8)cosxdx.

2. (7x 4)sin xdx.

3. (4x2 6x 3)sin2xdx.

4. (x3 4x 1)exdx.

5. (x 2)e3xdx.

6. x5ex2dx.

7. sinln xdx.

8. e2x cosxdx.

9. e3x sin6xdx.

10.

dx.

12. x3

dx.

11.

x2 2xdx.

1 x2

13.

14.

10)

§5. Интегрирование рациональных дробей

Рациональной дробью называют дробь вида P(x) , где Р(х), Q(х) –

Q(x)

многочлены. Рациональная дробь называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя. Напри-

мер, дроби

;

6x6 7x 1

– правильные, а дроби

2 2

x10 1

7x 6 8x

8x2 4x 1

;

14x3

;

7x6 1

– неправильные.

x 3

8x2 3

x4 2

Неправильную дробь можно преобразованиями или делением пред-

ставить в виде суммы многочлена (целой части) и правильной дроби.

Примеры:

8x2 4x 1

8x 20

x 3

целая часть

правильнаядробь

так как

								42				x 7
		14x3 7			14
							x			8
2.	. Поэтому												.
		8x	2	3		8			8x		2
												3
					целаячасть
								правильнаядробь

3.			7x6 1			7x2				14x2	1		, так как
3.						7x2							, так как
			x4 2							x4 2								.
			x4 2			целаячасть				x4 2								.
						целаячасть
								правильнаядробь
4.		x2 3			(x2 1) 4				x2 1			4			1	4		.
4.															1			.
		x2 1				x2 1			x2 1 x2				1				x2 1
		x2 1				x2 1			x2 1 x2				1		целая часть		x2 1

																правильнаядробь
5.	x 1			(x 8) 9			1							9	.
5.							1							x 8	.
	x 8					x 8								x 8
							целаячасть

правильнаядробь

Из сказанного понятно, что интеграл от всякой неправильной дроби сводится к интегралу от многочлена – целой части (считается легко) и к интегралу от правильной дроби. Поэтому далее нас интересуют методы интегрирования правильных дробей.

Прежде всего, напомним известные из алгебры теоремы о многочле-

нах.

Те о р е м а 1 . Чтобы число а было корнем многочлена Q(x), необходимо и достаточно, чтобы он делился без остатка на (х – а), то есть чтобы существовал такой многочлен R(x), что Q(x) (x a) R(x).

Те о р е м а 2 . Всякий многочлен Q(x) a0xn a1xn 1 ... an (отличный от постоянного) с действительными коэффициентами может быть

представлен в следующем виде:

Q(x) a0(x a) 1 (x b) 2 ...(x c) e (x2 p1x q1)S1...(x2 pr x qr )Sr ,

где а, b, … , с – действительные, различные между собой корни Q x ;

1,..., е – их кратности; многочлены x2 pix qi все различны между собой и не имеют действительных корней; S1,...,Sr – натуральные числа.

Причем 1 2 ... e 2 S1 ... Sr n.

Т е о р е м а 3 . Всякая правильная рациональная дробь P(x) может

Q(x)

быть представлена в виде суммы элементарных дробей:

P(x)																				P(x)
			a		(x											e (x			2						S			2	p x				q			)	S
Q(x)			a		(x	a)				1...(x c)						e (x				p x q ) 1...(x									p x				q		r	)		r
			0																		1			1						r					r
	A				A								A									A							B					B
	1					2						3					...						1		...				1						2
	x a			(x a)					2		(x a)				3		...								...			x c				(x c)						2
	x a			(x a)							(x a)											(x a)		1				x c				(x c)
	B3				...					B e				...						C1x D1							C2x D2
																										x2								2
	(x c)3							(x c) e										x2			p x q					x2		p x q						2
																					1			1					1				1
			CS x DS														K x M						1			K	2	x M			2
...					1					1			...						1				1				2				2
																									x2 prx qr								2
		x2		p x q S1												x2		prx qr							x2 prx qr								2
					1					1
...			KSr x DSr										,
...		x2		p		r	x q Sr						,
						r				r

где Ai,Bi,Ci,Di,Ki,Mi – действительные числа.

На практике данную рациональную дробь раскладывают на элементарные методами, которые мы изложим на примерах.

Примеры:	3x2
1. Разложим дробь		5x 12	на элементарные.

(x 1)(x 2)(x 3)

Выпишем сумму простейших дробей с неопределенными коэффициентами на основании теоремы 3.

3x2 5x 12

(приведем сумму дробей к

(x 1)(x 2)(x 3)

x 1

x 2

x 3

общему знаменателю) =

A(x 2)(x 3) B(x 1)(x 3) C(x 1)(x 2)

(x 1)(x 2)(x 3)

Из данного равенства видно, что первая и последние дроби совпадают. Так как у них одинаковые знаменатели, то и их числители равны:

3x2 5x 12 A(x 2)(x 3) B(x 1)(x 3) C(x 1)(x 2).

(2)

Далее А, В, С можно найти двумя способами.

1-й способ (метод неопределенных коэффициентов). Преобразуем равенство (2) к виду

3x2 5x 12 (A B C)x2 (A 2B 3C)x ( 6A 3B 2C).

Приравняем коэффициенты при одинаковых степенях х в обеих частях равенства, получим систему уравнений

A B C 3;

A 2B 3C 5;

6A 3B 2C 12.

Решив эту систему, найдем

A 5; B 14; C 27. 2 5 10

2-й способ (метод частных значений). В равенство (2) бу-

дем вместо х подставлять различные значения х и получать уравнения, связывающие неопределенные коэффициенты. Значения х подбираем так, чтобы получающиеся уравнения были максимально простыми:

при х = 2 уравнение (2) имеет вид

3 22 5 2 12 A 0 B(2 1)(2 3) C 0;

14 5B; B 14; 5

при х =1

3 12 5 1 12 A(1 2)(1 3) B 0 C 0;

10 4А; А 5; 2

при х = –3

3 32 5 3 12 A 0 B 0 C( 3 1)( 3 2);

54 20С;

Теперь мы можем выписать сумму простейших дробей:

3x2 5x

(x 1)(x 2)(x 3)

x 2

x 1

x 3

2. Разложить дробь

x3 2x 1

на элементарные. По тео-

(x 1)2(x 2)3

реме 3 имеем

x3 2x 1

(x 1)2(x 2)3

x 1

(x 1)

(x 2)

(x 2)3

x 2

A(x 1)(x 2)3

B(x 2)3 C(x 1)2(x 2)2

D(x 1)2(x 2) E(x 1)

(x 1)2(x 2)3

Выписываем равенство для числителей:

x3 2x 1 A(x 1)(x 2)3

B(x 2)3 C(x 1)2(x 2)2

D(x 1)2(x 2) E(x 1)2.

(3)

При х =1 получаем

13 2 1 1 A 0 B 33 C 0 D 0 E 0;

27B 2; B 2 . 27

При х = –2

( 2)3 2 ( 2) 1 A 0 B 0 C 0 D 0 E ( 3)2;

9E 5; E 5. 9

Теперь продифференцируем обе части равенства (3):

3x2 2 A(x 2)3	3A(x 1)(x 2)2	3B(x 2)2
2C(x 1)(x 2)2	2C(x 1)2(x 2) 2D(x 1)(x 2)
D(x 1)2 2E(x 1).		(4)

При х = 1

3 12 2 A 33 3B 32;

1 33		2		1
	A 27		;	A	.
		27
				9

При х = –2

3 ( 2)2 2 ( 3)2 D 2( 3)E;

10 9D 6E; 10 9D 6

;

Далее можно еще раз продифференцировать равенство (4) и

положить х = –2, однако, так как остался неизвестен только один

коэффициент, поставим в равенство (3) можно и в (4) некоторое

значение x, получим при х = 0

1 8А 8В 4С 2D E.

Используя найденные ранее коэффициенты, находим, что

Итак,

x3 2x 1

(x 1)2(x 2)3

9(x 1)

27(x 1)2

9(x 2)

27(x 2)

9(x 2)3

3. Разложить в сумму простейших дробей

x 1

x4 1

Разложим знаменатель дроби на простейшие множители:

x4 1 (x2 1)(x2 1) (x 1)(x 1)(x2 1).

Теперь воспользуемся теоремой 3:

x 1

Cx D

(x 1)(x 1)(x2 1)

x 1

x2 1

A(x 1)(x2

1) B(x 1)(x2 1) (Cx D)(x 1)(x 1)

(x 1)(x 1)(x2 1)

Выписываем равенство для числителей:

x 1 A(x 1)(x2 1) B(x 1)(x2

1) (Cx D)(x 1)(x 1).

При х = 1

2 A 2 2; A 1. 2

При х = –1

0 B( 2) 2; B 0.

При х = 0

1 A B D;

D A B 1;

D 1 0 1; D 1. 2 2

При х = 2

3 A 3 5 B(5 (2C D) 3;

3 15A 5B 6C 3D;

			3	15	5 0 6C				3	;
			3		5 0 6C				2	;
			2				1		2
			6C 3;C				1	.
			6C 3;C					.
			2
Итак,	x 1	1	x 1			.
Итак,	x4 1	2(x 1)				.
	x4 1	2(x 1)	2(x2 1)

4.Разложить в сумму простейших дробей 2x 3 .

x4 x

Знаменатель дроби нужно разложить на множители

2x 3

Cx D

x(x 1)(x2 x 1)

x4 x x(x3

x 1

x2 x 1

A(x 1)(x2

x 1) Bx(x2

x 1) (Cx D)x(x 1)

x(x 1)(x

2 x 1)

Отсюда 2x 3 A(x 1)(x2

x 1) Bx(x2

x 1) (Cx D)x(x 1).

При х = 0

3 3A;

A 1.

При х = 1

1 3B; B 1. 3

При х = –1

5 2A B 2(D C);

5 2 1 1 2(D C); 3

2(D C)		10	.	(5)
2(D C)		3	.	(5)
При х = 2		3
При х = 2
1 7A 14B 2(2C D);
	1	2(2C D);
1 7 1 14
1 7 1 14	3
	3

					2(2C D)											4		.				(6)
					2(2C D)													.				(6)
															3
Объединим равенства (5) и (6) в систему и решим ее:
															10
						2(D C)																;
						2(D C)																;
															3
																				4
																				4
						2(2C D)														3		.
																				3
Сложив равенства, получим																					7
					2C								14	; C							7		.
					2C									; C									.
							3													3
Теперь D C			10		; D	7			5		; D						12		;			D 4.
6				3			3								3
	2x 3	1			1					7		x 4
												x 4
Итак,								3							.
Итак,								x2 x 1							.
	x4 x x				3(x 1)			x2 x 1

По теореме 3 интегрирование всякой правильной рациональной дроби сводится к интегралам от простейших дробей четырех типов:

;

II.

, 1;

(x a)

x a

III.

ax b

dx;

IV.

ax b

dx; 1.

px q

px q)

Рассмотрим методы интегрирования этих дробей:

t x a;

C ln

x a

dx dt.

t 1

II.

t x a;

(x a)

dx dt.

(1 )(x

ax b

III. Интегралы

dx вычисляются

x2 px q

аналогично. Метод их вычисления разберем на примерах.

Примеры:

1.	3x 2	dx I.
	x2 2x 7

а) Выделяем полный квадрат в знаменателе:

x2 2x 7 (x2 2x 1) 1 7 (x 1)2 6;

	I		3x 2			.

		(x 1)2 6
б) Делаем замену x 1 t;dx dt; x t 1:
I	3(t 1) 2			dt	3t 5		dt.

	t2 6				t2 6

в) Записываем интеграл в виде суммы двух интегралов. Первый вычисляем с помощью замены, второй является табличным.

			tdt					dt			t2 6 k;								dk						dt		3				5				t
I 3						5					dk 2tdt;					3				2		5						ln		k			arctg
																				2

		t2 6					t2 6				tdt		dk		.					k			t2 6 2								6				6
		t2 6					t2 6						dk							k			t2 6 2								6				6
													2
													2
3					2			5					t					3						2		5						x 1
3					2			5					t					3						2		5						x 1
C			ln	t		6				arctg					C					ln	(x 1)				6				arctg					C
C			ln	t		6				arctg					C					ln	(x 1)				6				arctg					C
2								6					6					2								6					6
2								6					6					2								6					6
	2	ln(x2 2x 7)								5		arctg		x		1	C.
												arctg
									6
3									6				6

6x 2

Выделяемполныйквадратвзнаменателе:

2 4x

x2 4x (x2

4x 4) 4 (x 2)2 4

замена

6x 2

x 2 t;

6(t 2) 2

6t 14

tdt

(x 2)2

dx dt;

t2 4

x t 2.

d(t

t 2

3ln

t2 4

2 4

2 2

t 2

<<< < Предыдущая 1 23 / 153 4 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.2021321.16 Кб0163.pdf
#
07.01.20211.44 Mб31630.pdf
#
07.01.20211.44 Mб11631.pdf
#
07.01.20211.45 Mб201632.pdf
#
07.01.20211.45 Mб21633.pdf
#
07.01.20211.45 Mб21634.pdf
#
07.01.20211.45 Mб01635.pdf
#
07.01.20211.45 Mб01636.pdf
#
07.01.20211.45 Mб11637.pdf
#
07.01.20211.46 Mб241638.pdf
#
07.01.20211.46 Mб21639.pdf