
1282
.pdf
|
g ( p ' / = -arctg(*2 ). |
|
|
|
я |
О л |
|
|
|
|
|
|
Я |
= 1 => Л = 1. |
По условию — arctg(/r) = 0,5 => arctg(/r ) = — => Я |
||||
|
я- |
|
4 |
|
7 1 3 . |
Понятие |
о функции |
двух случайных |
величин |
Пусть имеется система двух случайных величин (X, Y) с плотностью вероятности j[x, у). Если <р(х, у) - числовая функция двух переменных, то случайная величина Z = <р(Х, У) называется функцией двух случайных величин X, У. Функция распределения случайной величины Z определяется
соотношением
Fz (z) = p{Z <z) = />(<Р(Л\ Y)) <z). |
|
|
|
(11.5) |
|
Покажем, как находится Fgfz) в случае суммы X + Y. |
|
|
|||
Fz(z) = p(X + Y<z) = p(X<x, |
Y<z-x), |
- о о < х < с о . |
|
||
Область |
х + у < z - это полуплоскость, ограниченная прямой |
х + у =] |
|||
= z (рис. 11.2). Значит, |
|
|
|
|
|
piX < |
х, Y < z - х) = J Z'(f(x, |
y)dxdy = J |
' ] / ( * • y)dy\dx. |
(11.6) |
|
|
—CO —CO |
-CO I -CO |
J |
|
|
Функция платности вероятности случайной величины Z равна |
|
||||
|
|
|
|
|
(П.7) |
Из соображений симметрии следует, что по-другому формулу для |
|||||
плотности вероятности f/{z) можно записать так |
|
|
|
||
/ z ( * ) = |
\f^-y,y)dy. |
|
|
|
(11.8) |
Если Хч Y - независимые случайные величины, сумму X + Y называют композицией законов распределения. Формулы (11.7) и (11.8) в этом случае
такие:
fz(z)= |
)f(x,z-x)dx= |
)fx(x)fY(z-x)dx= |
)fx(z-y)fY(y)dy. |
(11.9) |
—ОО |
—00 |
|
—00 |
|
Например, когда X к У распределены нормально с параметрами а*, C7r,ay>0y соответственно, можно показать, что их композиция X + также распределена нормально с параметрами (ax +aY )и (рх +<ТУ ) •
Рис. 11.2
11.4. Примеры решения задач
ПАЛ. Составить композицию двух случайных величин, равномерно
распределенных на отрезке (0, 1). Решение.
1, 0 < х < 1 ,
fx{x) =
0 в противном случае;
1, 0 < > ; < 1 ,
m =
Ов противном случае.
оо
Еслиг = Л ' + Г , т о / г ( г ) = jfx(x)fY(z - x)dx.
-со
Функция f\{x) отлична от нуля только при 0 < х < 1. Опишем функцию friz - х) при 0 < х < 1.
f 1, 0 < z - х < 1, friz -х) Н
[О в противном случае.
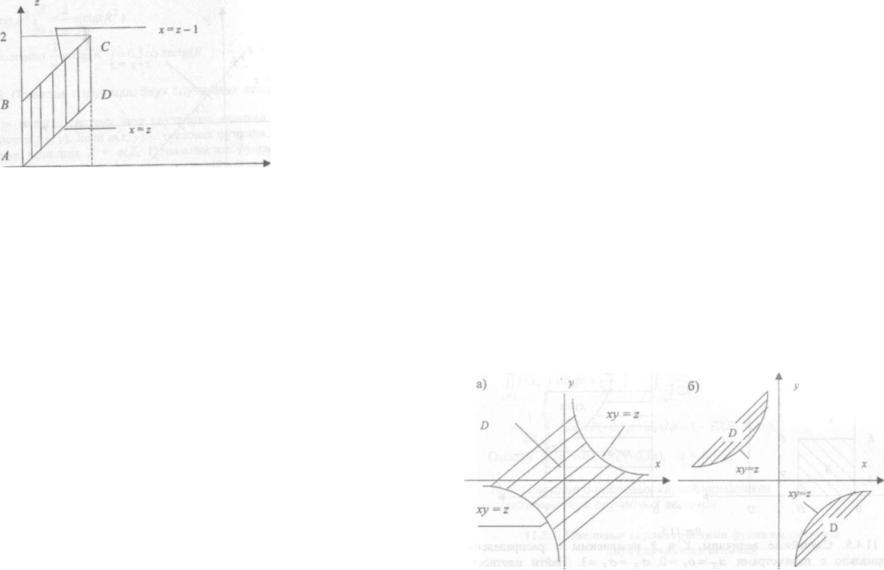
Так как 0 < х < 1, то неравенство 0 < z -х < 1 выполняется в полосе ABCD (рис. 11.3).
120 |
121 |
|
|
1 |
Рис.11.3 |
|
|
|
|
|
||
Таким образом, |
если z < О или z > 2, |
или х > 1, то fy(z - х) - 0. |
||
|
|
|
П, |
0 < x < z ; |
Е с л и ж е 0 < г < 1,то |
/ y ( z - x ) = <( |
|
||
|
|
|
0, z < x < l ; |
|
|
|
1, |
z - 1 < х < 1, |
|
К о г д а 1 < г < 2 , |
/ r ( z - x ) = 0, |
0 < x < z - l . |
||
Итак. |
|
|
|
|
О, |
|
z < 0 ; |
z > 2 ; |
|
z |
|
|
|
|
/ z ( * H \\dx = z, |
0 < z < 1; |
|
||
\\-dx = 2-z, \<,z<2.
U-i
11.4.2. Найти композицию независимых случайных величин А' и Y, если каждая из них имеет показательное распределение с параметрами Я,, Я2
соответственно.
х < 0 ,
х > 0 ;
У < 0,
[Я2е -^2*> _у > 0.
Решение. Положим z |
= х |
+ у, |
тогда / z ( z ) = |
(х)/у (z - х)<&. |
||
Плотность |
вероятности |
/^(х) |
отлична от нуля |
при х |
£ 0. Функция |
|
/ к ( z - х ) |
отлична от |
нуля, |
когда |
z - x > 0 = |
> z > x ^ > z > 0 . Таким |
|
образом, f7 (z) = 0, если z < 0. Пусть z > 0.
fz Ш = |
J/jr |
(* " |
= |Я, £АР(-Я, х)Я2 £АР(-Яз (z - x))dx = |
|
— о о |
|
|
- |
^1^2 |
£ A P ( - ^ z ) £ A 7 > ( - ^ - Я2)х) |
|
Я2 - Я,
я , я 2
(£АР(-Я, z) - £A7>(-^z)).
Я-j— Я)
а |
А |
|
В частности, если Я1 = Я2 = Я |
/z (z) = Л2е~Лг jdx =A2ze~Az, |
z > 0. |
|
о |
|
11.4.3. Задана плотность вероятности Дх, >«) системы (Af, |
Y) . Найти |
|
плотность вероятности случайной величины Z = АТ. |
|
|
Решение. Пусть Z = АТ, тогда Fz (z) = /?(Z < z) = p( AT < z ) . |
|
|
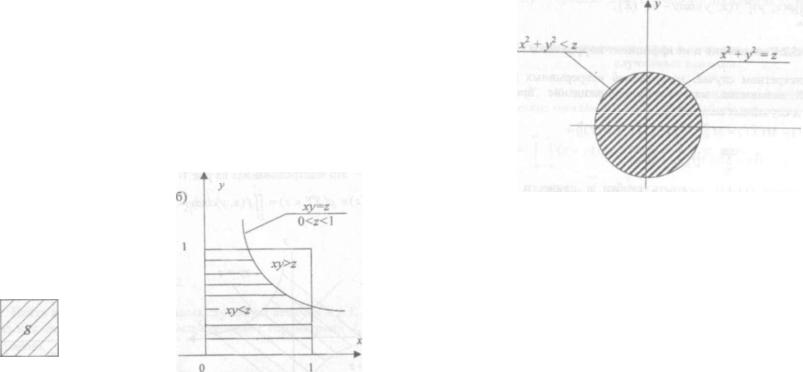
Множество точек плоскости, координаты которых удовлетворяют условию ху < z, - это заштрихованная на рис.14 область D.
Fz (z) = р( AT < z) = J]/(x, >0<fc<r> = J }/(*, у > й ф + J (fix, y)dxdy.
D - o o r / x 0 - o s
Z > 0 |
Z < 0 |
Рис.11.4
122 |
123 |
Если продифференцировать это выражение по z, получим
fz (*) = 4 Чг«= - J 1 |
я** -У*+11 Л * -V* • |
|||
Щ |
- с о Х |
Х |
0Х |
Х |
11.4.4. Координаты случайной точки (X, |
Y) распределены равномерно в |
|||
квадрате ABCD, длина стороны которого равна 1 (рис. 11.5, а). Найти закон распределения площади S прямоугольника AEFN со сторонами Л!" и Y.
Решение . Ясно, что F^z) = 0, если z < О, и F&) = 1, если z > 1. Рассмотрим значения z из интервала (0, 1) (рис.11.5, б).
Равномерное распределение системы (X, Y) внутри квадрата ABCD площади 1 означает, что
Г\,естО£х,у< 1;
[О в противном случае. Тогда, если 0 < z < 1,
1 1
Fs(z) = p(S <z) = p(XY < z) = 1 - \dx \dy = z(l - In z).
z tlx
Отсюда
-lnz, если 0 < z < 1,
Ов противном случае.
a)
о |
н |
О |
Рис.11.5
11.4.5. Случайные величины X и Y независимы и распределены нормально с параметрами ах = ау = О, ах = о> = 1. Найти плотность
вероятности случайной величины Z = X +Y . Решение.
Fz(z) = p(Z < z) = p(A"2 + Г2 < z) = 0, если z < 0. Пусть z > 0, тогда
124
/ H A ' 2 + r ' 2 < z ) = \\f(x,y)dxdy.
где /? - круг радиуса Vz с центром в начале координат (рис. 11.6).
Л*. = fx Шг (У) = - 7 = |
ЕХР(-0,5х2) -i £*Р(-0,5 у 2 ) = |
V2;r |
>/2л- |
2л- £АР(-0,5(х2 + / ) ) .
Положим х = р cos _у = р sin .
¥• X
|
|
|
|
Рис.11.6 |
|
|
|
1 |
л |
|
1 |
J |
J/(x, |
= — |
J |
I |
— £A7>(-0,5(x2 4 .у2 ))dxdy = |
= — J J/7£^/J (-0,5p2 )^9 ) = l-£W>(-0,5z).
|
о о |
|
|
|
Отсюда fz (z) = 0,5£A7>(-0,5z), z > |
0. |
|||
77.5. |
Понятие |
о |
числовых |
характеристиках |
системы |
двух |
|
случайных |
величин |
11.5.1. Числовые характеристики функции системы двух случайных величин
Если Z = <р(Х, Y) - функция двух непрерывных случайных величин X и Y, то математическим ожиданием величины Z называется число, определяемое формулой
125

M(Z) = M[<p(X, Y)} = \ \<p(x, y)f(x, y)dxdy. |
(1110) |
—00 —00
Интеграл (11.10) предполагается сходящимся абсолютно. Дисперсией
случайной величины Z называется число
D(Z) = ф ( Л \ Y)]= J ][«Кх, у)-M(Z)]2f(x, y)dxdy. |
(11.11) |
- 0 0 —00
Если в формуле (11.11) раскрыть скобки и привести подобные, то
получится следующая формула: |
|
1XZ) = ] )[<р{х, у)]2 /(х, y)dxdy -M2(Z). |
(П.12) |
-ее -со |
|
11.5.2.Ковариация и коэффициент корреляции
Как и в дискретном случае, ковариацией непрерывных случайных величин X, Y называется математическое ожидание произведения
центрированных случайных величин |
X, Y. |
|
|
|||||
|
Cov(X, Y) = М(АТ) = Л ф Г - M(X)lY - M(Y)} = |
|
||||||
|
= |
] |
\x-M{X)[y-M(Y)]f(xt |
y)dxdy. |
|
|
(11.13) |
|
|
|
- 0 0 |
- 0 0 |
|
|
|
|
|
|
Если в формуле (11.13) раскрыть скобки и привести подобные, |
|||||||
выражение для ковариации станет таким: |
|
|
||||||
Cov(X,Y)= |
J |
)xyf(x,y)dxdy-M(X)M(Y) |
|
|
||||
|
|
|
— s o - C O |
|
|
|
|
|
M(XY)- |
|
M(X)M(Y).(\\.\A) |
|
|
|
|
||
|
Поясним переход от формулы (11.13) к формуле (11.14) чуть |
|||||||
подробнее. Например, |
|
|
|
|
|
|||
СО |
ОС |
|
|
СО |
СО |
00 |
оо |
|
J |
\ |
xM(Y)f(x, y)dxdy |
= M(Y) |
J f |
x/(x, yyJxdy = |
M(Y) j |
xdx J/(x, y)dy |
|
|
|
|
|
|
|
|
- 0 0 |
—00 |
= |
M(Y) |
jxfx(x)dx = |
M(Y)M(X). |
|
|
|
||
|
|
—CO |
|
|
|
|
|
|
Когда ЛГи Y независимы, то Cov(A\ У) = 0, ведь в этом случае
/(х,у) = /х(х)/у(У)**
Cov(A\ Y)= ] )xyfx(x)My)dxdy-M(X)M(Y) =
3 0 |
со |
|
= |
\xfx{x)dx |
lyfy(y)dy-M(X)M(Y) = M(X)M(Y)-M(X)M(Y) = 0. |
- S O |
- c o |
|
Обратное утверждение неверно, Cov(Ar,K) может равняться нулю, хотя X и Y- независимые случайные величины. Пример уже был приведен
для дискретного случая.
Коэффициентом корреляции случайных величин A", Y называется число
р{Х, Y) - |
—• |
, |
|
(11.15) |
|
<Т |
v |
(Ту |
' |
где сгх, а у - средние квадратические |
отклонения |
случайных величин |
||
X, Y. |
|
|
|
|
11.5.3. Математическое ожидание и дисперсия суммы непрерывных случайных величин
Пусть X, Y - непрерывные случайные величины, имеющие
математические ожидания и дисперсии. Найдем математическое ожидание их суммы
|
|
|
о о |
о о |
во |
со |
ас х |
|
M(X |
+ |
Y)= |
\ |
\(x + |
y)f(x,y)dxay= |
j |
j xf(x,y)dxdy + |
J \yf(x,y)dxdy = |
|
|
|
— CO —CO |
|
|
— 0 0 — CO |
— 0 0 — CO |
|
X |
|
Ж |
|
SO |
CO |
CO |
CO |
|
= |
j |
xdx |
J |
Ax,y)dy+ |
\ydy jf(x,y)dx= |
LXFx(x)dx+ |
jyfy{y)dy = |
|
—«о |
|
—оо |
|
-во |
— с о |
—ее |
—со |
|
= M(X) + M(Y); |
|
|
|
|
||||
|
|
|
|
M(X + Y)=M(X)+M(Y). |
|
(Ц.16) |
||
Как и в случае дискретных случайных величин, найдем дисперсию суммы
D(X±Y) = М(Х ± Y)2 -M2(X±Y) = М(Х2 +Y2 ± 2XY) -
-[М{Х)± M(Y))2 = М(Х2) + M(Y2)± 2M(XY)-М2(Х) - Л/2(К)±
±2M(X)M(Y)=D(X) + D(Y)±2Cov(X, Y), |
(11.17) |
что также совпадает с результатом для дискретного случая.
Когда случайные величины X и Y независимы, их ковариация равна нулю, а ГХХ± Y) - ГХ.Х) + D(Y).
Если слагаемых не два, а п, то формула (11.12) обобщается так:
^ i ^ ) = i ^ / ) + 2 Z C o v ( A ' / , A ' y ) . |
( Ц . 1 8 ) |
||
I |
I |
i,j>i |
|
126 |
127 |
|
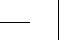
11.5.4. Свойства коэффициента корреляции |
|
Доказательство того, что |
|
|р(А, У)| < 1 и р(Х, У) = 1 о у = аХ + Ь |
(11.19) |
подобно уже проведенному для случая дискретных случайных величин .
11.6. Примеры |
решения |
задач |
|
11.6.1. Даны две независимые случайные величины X, |
У. Величина X |
||
распределена по нормальному закону с параметрами a = 1; |
a = 2. Величи |
||
на У равномерно распределена на отрезке [0, 2]. Определить: М(Х + У),
М(АУ), MiX2), MiX-У2), DiX+ У), DiX-Y).
Решение. Дано, что MiX) = 1, Д А ) = 4, М(У) = 1, Д У ) - 1/3.
Тогда MiX + У) = MiX) + Л/(У) = 2; Л/(АУ) - Л/(А)М(У) - 1; ЩХ2) = ДАТ + Л/ЧА) = 5; Л/(^) = Д Г ) + Л^У) = 4/3; Л/(А - Г2) = Л/(А) - ЩУ2)
=-1/3; ДА" + У) = Д А ) + Д 1 ? = 13/3; ДА" - Y) - Д А ) + Д К) = 13/3.
11.6.2.Случайные величины А и У имеют математические ожидания MiX) = - 1 , Л/(У) = 3. Ковариация этих величин равна 6.
Найти математическое ожидание случайной величины Z = ЗАУ + 4.
Решение. M(Z) - Л/(ЗАУ + 4) = ЗЛ/(АУ) + 4= 3[Cov (А, |
+ Л/(А)Л/(У)] + |
+4 = 13.
11.6.3.Из истории мер. Мера длины фут, как видно из названия, имеет прямое отношение к ноге. Это - длина ступни. Но, как известно, размеры ног бывают разные. Немцы в XVI в. выходили из положения следующим образом. В воскресный день ставили рядом 16 первых вышедших из церкви мужчин. Сумма длин их левых ступней делилась на 16. Средняя длина и была «правильным и законным футом». Известно, что размер стопы взрослого мужчины - случайная величина А, имеющая нормальное распределение со средним значением a = 262,5 мм и средним квадратическим отклонением a = 12 мм. Найти вероятность того, что два «правильных и законных» значения фута, определенных по двум различным группам мужчин, отличаются более чем на 5 мм. Сколько нужно было бы взять мужчин, чтобы с вероятностью, большей 0,99, средний размер их ступней отличался от 262,5 мм менее чем на 0,5 мм?
Решение. Сумма попарно независимых случайных величин, имеющих нормальное распределение, также нормально распределена. Математическое ожидание и дисперсия этой суммы равны соответственно сумме математических ожиданий и сумме дисперсий слагаемых. Тогда случайная величина А - сумма длин левых ступней 16 случайно
отобранных мужчин - имеет нормальное распределение с математическим | ожиданием, равным 16-262,5 мм? и дисперсией, равной 16-122 мм2,
Случайная величина У = А/16 нормально распределена, и М(У) = 262,5 мм, П(У) = 144/16 мм2, = 9мм2, oiY)= 3 мм.
Разность двух таких независимых и одинаково распределенных случайных величин Z = У| - У2 имеет нормальное распределение с математическим ожиданием, равным нулю, и дисперсией, равной 9 + 9 = = 18 мм2, о\Т) = 3 -Jl мм. Нужно найти вероятность p(|Z| > 5.). Имеем
pi\Z\ < 5) =2Ф(~4=)= 2Ф(1,18) = 0,762. Искомая вероятность - это вероят3V2
ность противоположного события, она равна разности 1 - 0,762 = 0,238.
)
р\\ 262,5 <0,5
1
и среднего квадратического отклонения случайной величины —.
р\\— -262,5 <O,5J = 20j |
> 0,99. Но тогда о/ Л |
> 0,495, откуда |
12 |
24 |
|
— > 2,58 => л £ 3 8 3 4 . 24
11.6.4. Случайные величины А и У равномерно распределены на отрезке (0, 1). Доказать, что при любом характере зависимости между величинами А и У имеет место неравенство ЫЛХ - У|) £ 0,5.
Решение. Воспользуемся неравенством |х + > | & |х| + \у\.
|
п |
|
|
|
11 |
|
|
ЩХ-У|)=| J|x - y\fix, |
y)dxdy = |
|
/ J|x - 0,5 |
+ 0,5 - у\Дх, y)dxdy <, |
|
|
00 |
|
|
|
00 |
|
1 |
1 |
1 1 |
|
|
|
|
< |
J J|x - 0,5|/(x, y)dxdy + |
j /10,5 |
- |
y\fix, y)dxdy |
= |
|
00 |
00 |
|
|
|
|
|
= J|x - 0,5|*x J/(x, y)dy |
+ |
J|0,5 |
- |
y\dy\fix,y)dx = |
||
0 |
0 |
0 |
|
|
0 |
|
1 |
|
1 |
|
|
1 |
1 |
= J|x - 0,5|/* ix)dx + J|0,5 - y\fY iy) = \\x - 0,5\dx + j\y - 0,5|<r> = 0,5.
0 |
0 |
0 |
0 |
128 |
129 |
|

Следовательно, p(\Xx - p\ < e) £ 1 |
|
|
j. |
|
||||
|
|
|
||||||
В случае, когда существует MiX2), получается неравенство |
|
|||||||
P(X2<e2) |
= |
pi\X\<e)>l-^P. |
|
|
(12.3) |
|||
Неравенство Чебышева универсально, поэтому оценка вероятности, |
||||||||
которую оно дает, очень груба. |
|
|
|
|
|
|||
12.2. |
Понятие |
о |
законе |
больших |
|
чисел |
|
|
Будем говорить, что для |
последовательности случайных |
величин |
||||||
Х],Х2,—,Хп. |
..(*), |
имеющих |
математические |
ожидания |
||||
М(ХХ), М(Х2),—, |
М{Х „)..., выполняется |
|
закон больших чисел, |
если для |
||||
любого сколь угодно малого Е > 0 при я -> СО справедливо предельное соотношение
I |
п |
1 п |
|
|
1, я -> оо. |
|
|
|
(12.4) |
||
|
|
|
|
|
|
|
|
|
|||
Другая запись: |
|
|
|
|
|
|
|
|
|||
1 S |
1 В |
> f |
- >0 , я - ю о . |
|
|
|
(12.5) |
||||
Р |
|
|
|
|
|
|
|||||
, |
Я | |
|
|
|
|
|
|
|
|
||
Я |
|
|
|
|
|
|
|
|
|||
Если для последовательности случайных величин Z,, |
Z2,..., |
Z„,... для |
|||||||||
любого е |
> |
О оказывается, |
|
что |
lim pi\Z„ - а\ > е) = О, где а - некоторое |
||||||
число, то |
последовательность |
случайных |
величин |
Z,, Z2 |
Z„... |
||||||
называется сходящейся по вероятности к числу а. |
|
|
|
||||||||
Таким |
образом, для |
|
последовательности |
случайных |
величин |
||||||
Хх, Х2,...,Хп... |
выполняется |
закон |
больших |
чисел, |
если |
среднее |
|||||
|
|
|
|
|
|
|
1 " |
|
|
|
|
арифметическое |
случайных |
|
величин |
— £ Х{ |
сходится по вероятности к |
||||||
|
|
|
|
|
|
|
п 1 |
|
|
|
|
среднему |
арифметическому |
-^М(Х,) |
математических |
ожиданий этих |
|||||||
|
|
|
|
|
я |
|
|
|
|
|
|
случайных величин. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
л |
|
|
Теорема А.А. |
Маркова. Обозначим |
через |
Sn сумму £ Х(. Если |
||||||||
I
®(^»} _> 0, и ->' оо, то закон больших чисел справедлив для
последовательности (*).
Теорема Чебышева. Если случайные величины ХХ,Х2,...,Х„... попарно независимы, имеют конечные математические ожидания и равномерно ограниченные дисперсии, т.е. D(Xn)<L, где L - заданное число, независящее от я, то для последовательности (*) выполняется закон больших чисел.
Теорема Чебышева следует из теоремы Маркова. Ведь в силу попарной
независимости случайных величин |
Хх,Х2,...,Хп... |
|||||||||
|
|
— = |
|
ft |
- |
- = |
|
г |
~~7= |
* 0> |
|
|
|
|
|||||||
|
Я |
|
|
Я |
|
Я |
П |
|||
Всвою очередь, теорема Маркова получается из неравенства
Чебышева. Пусть условия теоремы Маркова выполнены, т.е. |
-> О, |
||||
|
Lj |
|
|
я |
|
|
S- |
1 |
|
||
я-» со. Положим |
Z„ |
= — . |
Тогда D{Zn) = — D(Sn)-> 0, я -> со. |
|
|
|
|
|
« |
я2 |
|
Но в силу неравенства Чебышева |
|
||||
М |
> |
* |
) = |
/ , ( | Z „ - M ( Z j | ^ ) < : ^ ^ - » ( ) , |
я - > о о . |
Покажем, что закон больших чисел применим для схемы Бернулли. Пусть X - случайная величина, которая равна 1, если в / - м испытании произошел "успех", и равна нулю в противном случае. Тогда М(Х{) = р, а ЩХ,) = pq <, 1, так как 0 < р, q <, 1.
Случайные величины Xi попарно независимы, поэтому выполнены условия теоремы Чебышева - к последовательности Хх, Х2, Хп...
применим закон больших чисел:
i n |
i n |
<£•)->!, |
я СО. |
|
|
|
Pi - 5 > , - - 2 > ( * , ) |
|
|
|
|||
]" »I |
И 1\ п |
|
|
п |
|
|
Но - У А Г Ш А - У В А И , а случайная величина |
А |
Г = У Л |
Г . - это |
|||
* г ' |
И |
|
|
1 |
|
|
число появлений "успеха" в я независимых испытаниях, следовательно,
/К — р' < Е) -> 1, Я - » СО .
я |
|
Случайная величина |
это относительная частота появления |
я
"успеха" в я независимых испытаниях. Итак, при я -> СО относительная частота появления "успеха" в я независимых испытаниях сходится по вероятности к вероятности р появления "успеха" в одном испытании.
132 |
133 |
72.3. |
Понятие |
о |
центральной |
предельной |
теореме |
В центральной предельной теореме описываются условия, при которых возникает нормальный закон распределения. Оказывается, что он возникает всякий раз, когда случайная величина может быть представлена в виде суммы достаточно большого числа попарно независимых случайных величин, каждая из которых сравнительно мало влияет на всю сумму.
Пусть случайные величины А,, Х2, X „...(*) попарно независимы
и каждая из них обладает математическим ожиданием и дисперсией:
п
М(Х[) = я , , D{Xj ) = of . Обозначим через Sn сумму £ А , , через А„ сумму
|
«=| |
, через Вп сумму |
£<т, . |
ы |
/=1 |
Будем говорить, что к последовательности (*) применима центральная |
|
предельная теорема, если для любых чисел fj и t2 при п -» ю справедливо |
|
предельное соотношение
S.-A. -</2)->-= \е 2 dt, п ->оо.
е д
иными словами, при п ->« случайная величина S„ имеет приближенно нормальное распределение с параметрами а = Ап и o~ = <yfii^.
Теорема Ляпунова. В этой теореме устанавливаются достаточно общие условия, выполнение которых влечет применимость центральной предельной теоремы к последовательности (*). Эти условия охватывают большинство практических случаев.
Будем дополнительно предполагать, что у случайных величин А} существуют абсолютные центральные моменты третьей степени
Af(|A,|3) = С,. Если для последовательности (*) справедливо предельное
соотношение |
5 = |
|
-•О, |
и - » со, |
то для |
последовательности (*) |
||
|
|
/=1 |
|
|
|
|
|
|
справедлива и центральная предельная теорема. |
|
|
|
|||||
Можно |
показать, |
что |
если |
А,, А2, |
А„ ... - |
одинаково |
||
распределенные |
и |
независимые |
случайные |
величины, |
то |
для |
||
последовательности (*) справедлива центральная предельная теорема. |
|
|||||||
12.4. Локальная и интегральная теоремы Лапласа
Случайные величины Щ , введенные при рассмотрении схемы Бернулли, независимы и одинаково распределены с математическим
ожиданием |
М{Х) - р |
и дисперсией |
a? = pq, a, =4pq. Таким образом, |
|
|
п |
|
случайную |
величину |
А = £ А",- - |
число появлений "успеха" в п |
|
|
i=\ |
|
независимых испытаниях - можно считать при больших п приближенно
нормально |
распределенной с |
математическим ожиданием а = пр и |
дисперсией |
а2 = npq, а = Jnpq. |
Тогда при больших п вероятность |
события {А - к) можно приближенно положить равной значению функции плотности вероятности в точке х = к .
|
j |
-(*-чр)2 |
|
|
||
|
j |
|
|
|
Если обозначить |
через x |
Pn(k) = Р(Х = k)*—r |
e 2npq . |
|||||
|
^iKyjnpq |
|
|
|||
выражение - ^ Ж , то |
Pll(k) = -==q>(x), где |
<p(x) = -1L=e * |
- функция |
|||
V"W |
|
y/npq |
Jbc |
|
||
плотности вероятности центрированного и нормированного нормального распределения. Этот результат называется локальной теоремой Лапласа.
Вероятность события л, < А < к2 (< или < - это неважно) при больших значениях п можно вычислить через значения функции Лапласа
р(кх |
< |
А |
<к2)*Ф |
-Ф |
А, - пр |
= Ф(х2)-Ф(х{), |
(12.6) |
||||||
|
|||||||||||||
|
|
|
|
|
|
|
yjnpq |
|
|
|
|
||
, я е г - |
к х ~ п р |
г |
- к 1 ~ п р |
|
|
|
|
||||||
i де X] - |
. |
|
|
. , х2 - —. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||||
Этот |
yjnpq |
|
Jnpq |
интегральной |
теоремой Лапласа. |
|
|||||||
результат |
называется |
|
|||||||||||
Выведенные формулы дают хорошее приближение к истинным значениям вероятностей тогда, когда п достаточно велико (50 и более), а вероятность р не слишком отличается от 0,5 в ту или иную сторону. Практически можно судить о возможности замены биноминального распределения нормальным по тому, выполнены ли при данных пир условия
пр - 3^npq > 0; пр + З-yJnpq < п.
Эти условия основаны на "правиле трех сигм" для нормального закона (см. 10.8.6), когда они соблюдены, можно пользоваться нормальным распределением.
134
135
72.5. |
Примеры |
решения |
задач |
|
|
|
|
12.5.1. Дисперсия каждой из попарно независимых случайных |
|||||||
величин не превышает 10. Требуется: |
|
|
|
||||
а) Оценить |
вероятность |
того, |
что модуль |
отклонения |
средней |
||
арифметической |
X |
шестнадцати |
тысяч этих |
величин |
от ее |
||
математического ожидания не превышает 0,25. б) Определить, сколько таких случайных величин нужно взять, чтобы с вероятностью, не меньшей
0,995, можно было утверждать, что |
абсолютная величина разности X - |
|||||||||
М(Х ) не превысит 0,25. |
|
|
||||||||
Решение. Гак как дисперсия суммы попарно независимых случайных |
||||||||||
величин равна сумме дисперсий слагаемых, то |
|
|||||||||
|
D(X) = D((A, + Х2 |
+ ...+ Xn)ln) = \/n2D(X] + Х2+... + Х„) = |
||||||||
|
- 1 / W 2 £ D ( , Y , ) < ( 1 / w 2 ) - 1 0 , 7 = 1 0 / w . |
|
||||||||
|
|
|
М |
|
|
|
|
|
|
|
|
По условию задачи |
D(X,) < 10 для всех /, тогда |
|
|||||||
|
р(\Х - M(Xi < |
0,25) |
£ 1 - 5Щ > |
10 |
= 0,99. |
|||||
|
1 - |
|||||||||
|
|
|
|
|
|
|
|
0,25' |
16000-0,25' |
|
|
Чтобы ответить на второй вопрос, нужно определить число п |
|||||||||
случайных величин из условия |
|
|
||||||||
|
1 |
|
—- > 0,995, |
откуда п > 32000. |
|
|||||
|
|
|
||||||||
|
|
п• |
0,25 |
|
|
|
|
|
|
|
|
12.5.2. Оценить вероятность того, что при 3600 независимых бросаниях |
|||||||||
кубика число появлений 6 очков будет не меньше 900. |
||||||||||
|
Решение. Случайная величина X - число появлений 6 очков в 3600 |
|||||||||
бросаниях кубика - имеет математическое ожидание |
|
|||||||||
М(Х) = 3600 |
- = 600. |
Тогда по неравенству Чебышева при е= 900 имеем |
||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
600 |
2 |
|
|
|
|
|
900) < |
|
|
|
= - . |
|
|
|
||
|
|
|
|
|
|
|
||||
ИК |
|
|
|
|
900 |
3 |
|
|
|
|
|
Вычислим ту же вероятность, используя интегральную теорему |
|||||||||
Лапласа. |
|
|
|
|
|
|
|
|
||
|
р = 1/6; q = 5/6; пр = 3600-1/6 = 600; npq = 600-5/6 = 500; jnpq = 22,36; |
|||||||||
it, = 900; |
А2=3600; |
^ £ = 13,42; |
^ ^ = 134,16; |
<f> (134,16) = 0,5; |
||||||
|
|
|
|
|
|
|
jnpq |
yjnpq |
|
|
Ф (13,42) |
= |
|
0,5. |
|
Так |
что искомая вероятность практически равна 0. |
||||
Неравенство Чебышева дало очень грубую оценку. |
|
|||||||||
12.5.3. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента равна 0,05. Оценить вероятность того, что модуль разности между числом отказавших элементов и средним числом отказов окажется не меньше двух.
Решение. Пусть X - число отказавших элементов. Тогда е = 2; « = 1 0 ; р = 0,05; 9 = 0,95; Л/(А> пр = 0,5; D(X)= npq = 0,475.
£4
Пользоваться нормальным законом распределения в этом случае нельзя, так как вероятность р мала, кроме того, ст{Х) = ^0,475 = 0,689; Зо\Х) = 2,07; пр - Ъо\Х) = 0,5 - 2,07= -1,57 < 0.
Если бы мы подсчитывали число работающих элементов, то вероятность р равнялась бы 0,95, и тогда пр + За(Х) = 9,5 + 2,07 = \2,2>п.
12.5.4. Оценить вероятность того, что частота появления "шестерки" в 10 000 независимых бросаниях кубика отклонится от вероятности появления "шестерки" по абсолютной величине меньше чем на 0,01.
Решение. Если X - число появлений "шестерки" в п независимых бросаниях кубика, то частота появления "шестерки" - это случайная
величина |
—. Отсюда, если п - 10 000, |
р = 1 /6, |
а = 516, е - 0,01, то |
|||||||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
5 |
|
|
|
|
|
10 000 |
- - < 0 , 0 1 |
>1 |
|
|
|
|
= 0,861. |
|
||
|
|
|
|
|
||||||
6 |
10 000 |
0,01 |
|
|
|
|||||
|
|
|
|
|
|
|||||
В соответствии с |
центральной |
предельной теоремой |
мы можем |
|||||||
|
|
|
|
|
|
X |
|
|
|
|
считать, |
что |
случайная величина |
|
— |
имеет |
приближенно |
нормальное |
|||
|
|
ш |
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
распределение с математическим ожиданием, равным р = -, и дисперсией, |
||||||||||
равной |
-^ = - ^ ^ = 0,0000138. |
Тогда |
= д/0,0000138 = 0,00373; |
|||||||
Зсг(^) = 0,011; |
р - За(—) = 0,155 > 0; |
р + З а ( — ) = 0,178 < 1; |
||||||||
п |
|
|
|
п |
|
|
|
|
|
п |
X |
1 |
< 0,01 Цз4-Й |
|
= 2Ф(0,2,68) = 0,9926. |
|
|||||
10 000 |
6 |
J |
1о,о( |
|
|
|
|
|
|
|
|
00373, |
|
|
|
|
|
|
|||
12.5.5. Вероятность появления события А в каждом испытании равна 0,5. Оценить вероятность того, что в 100 независимых испытаниях событие А появится от 40 до 60 раз.
136 |
137 |
Решение. Случайная величина X - число появления события А в 100 независимых испытаниях - имеет биноминальное распределение с математическим ожиданием М(Х) - 1001/2 - 50 и дисперсией
D(X) = 100 - — - — = 25. Значит, нужно оценить вероятность события
р(\ X - 50| < 10). Следовательно,
р(\Х-50| < 10) > 1 - ^ = 0,75.
Использование нормального закона дает такой результат:
р(|Л--50|<10) = 2 Ф | У = 0,9544.
Число опытов п невелико, поэтому снова получается большое расхождение с оценкой по неравенству Чебышева.
Между тем пр±За(Х) = 50±15; 35 > 0; 65 < 100, поэтому применение
центральной предельной теоремы правомерно.
При решении следующих задач подразумевается возможность использования нормального распределения.
12.5.6. Монета брошена 2N раз (N велико). Найти вероятность того, что
герб выпадает ровно N раз. |
|
|
Решение, п = 2N, к = N, p-q = 0,5; |
х = Ц |
= 0. Так как ф) = |
= 0,3989, имеем р„(к) « |
|
|
V27V - 0,25 |
VN |
JN |
12.5.7. Вероятность появления некоторого события А в каждом из 2100 независимых испытаний равна 0,7. Найти вероятность того, что это событие появится: а) не менее 1470 и не более 1500 раз; б) не менее 1470 раз; в) не более 1469 раз.
Решение. Воспользуемся интегральной теоремой Муавра - Лапласа.
а) |
По условию А, = 1470, к2 =1500, п = 2100, р = 0,7, |
q = 0,3. Тогда |
||||
m> = 1470, > 7 W = 441, |
^w = 2 1 ; x I |
= J r = £ - = 0, |
х2 = |
\ |
=1,43. |
|
По |
таблице значений |
функции |
Лапласа |
Ф(х) |
(см. |
приложение |
определяем, что Ф(0) - 0, Ф(1,43) = 0,4236. Тогда искомая вероятное
равна |
|
|
p(ks |
< X <,к2) = |
Ф(х2)-Ф(х,) = 0,4236. |
б) Событие А должно появиться не менее 1470 раз, но оно не мож |
||
появиться |
более 2100 |
раз, поэтому л, = 1470, к2 = 2100, х, = |
*2 |
_ 2100-2100 0,7 ,л |
_ |
|
|
|
|
||||
|
— |
|
|
30. Так как для всех значений аргумента х функции |
||||||
|
|
|
||||||||
Лапласа, больших |
пяти, |
можно |
считать, |
что Ф(х) = 0,5, |
получаем, что |
|||||
р( 1470 < X < 2100) = Ф(30) - Ф(0) = 0,5. |
|
|
|
|||||||
|
в) События |
{событие А появилось не менее 1470 раз} |
и |
{событие А |
||||||
появилось |
|
не |
более |
1469 |
раз} |
противоположны, |
поэтому |
|||
р(Х < 1469) =\-р(Х* 1470) = = 1 - 0,5 = 0,5.
12.5.8.Вероятность появления положительного результата в каждом из
попытов равна 0,8. Сколько нужно произвести опытов, чтобы с вероятностью 0,9 можно было ожидать, что не менее 75 опытов дадут положительный результат?
Решение. По условию р = 0,8, q = 0,2, х, = 75, к2 = п, р(Х > 75) = 0,9. Нужно найти п. Таким образом, р(Х £ 75) = р(75 < X < п) = <Z>(x2 ) - Ф(х,),
|
|
75-0,8w |
|
75-0,8« |
л - 0,8 л |
|
(п |
|
|
||
ГДе |
~ |
/„ по |
|
~ л / Г ' |
*2 = п |
л |
г- |
= л - • Очевидно, что п > 75, |
|||
|
|
Vw- 0,8 0,2 |
0,4Vп |
0 |
, |
4 |
V |
2 |
|
|
|
поэтому yjojn > д/37,5 = 6,12. |
|
|
|
|
|
|
|
||||
Можно положить, что ФЦп/2) = 0,5, |
тогда |
0,9 = 0,5 - Ф |
/ 75 - 0,8и |
га |
|||||||
|
|
|
|
|
|
|
|
|
|
0,47й |
|
|
|
|
|
|
|
|
|
|
|
|
|
есть |
Ф 75-0,8м |
= -0,4. По |
таблице |
функции Лапласа |
находим, что |
||||||
|
|
0,4л/я |
|
|
|
|
|
|
|
|
|
api-умент, для которого функция Лапласа равна 0,4, равен |
1,26. Функция |
||||||||||
Лапласа |
нечетна, |
поэтому |
Ф(-1,28) = -Ф(1,28) = -0,4. |
Окончательно |
|||||||
75-0,8w |
j ло |
_ |
с |
г |
|
|
|
|
|
|
|
0 4-/Й |
= ~ ' |
|
обозначить у |
и |
через |
х, получается квадратное |
|||||
уравнение 0,8х2 - 0,512х - 75 = 0, откуда х, 2 = 0 , 5 1 2 ± 1 5 ' - . 1,6
_ Так как корень не может быть отрицательным, остается одно значение: Vw"= 10; л = 100.
12.5.9. В очереди на получение денег в кассу стоят п = 60 человек; размер выплаты каждому из них случаен. Средняя выплата X = 500 руб., среднее квадратическое отклонение выплаты <г0 = 200 руб. Выплаты отдельным получателям независимы. Сколько должно быть денег в кассе, чтобы их с вероятностью 0,95 хватило на выплату всем 60 получателям? Каков будет гарантированный с той же вероятностью 0,95 остаток денег в кассе после выплаты всем 60 получателям, если в начале выплаты в кассе было 35000 руб.?
138
139
Решение. Подразумевается, что случайная величина X - суммарная выплата 60 получателям - есть сумма 60 независимых, одинаково
распределенных случайных величин. На |
основании |
центральной |
предельной теоремы для одинаково распределенных слагаемых величину X можно считать приближенно нормально распределенной с параметрами
а= 60-500 = 30 000 руб. и <т = 200л/б0 * 1549руб.
Пусть х - необходимый запас денег. Он определяется из условия р{Х>
|
(х-Ъ0Шл |
||
> х) * 0,05 или р(х < Х< со)- 0,05. Тогда Ф\ |
|
= 0,45. По таблице |
|
t 1549 , |
|||
|
|||
функции Лапласа находим, что - — - — * - - = 1,65; х = 32 556 руб. Остаток 1549
денег в кассе равен разности 35 000 - х = 35 000 - 32 556 • 2444 руб.
Библиографический список
1. Аидрухаев ХМ. Сборник задач по теории |
вероятностей. - М . : Просвещение, |
1985. |
|
2. Беррондо М. Занимательные задачи. - М.:Мир, 1983. |
|
3. Вентцель Е.С. Прикладные задачи по |
теории вероятностей / К . С . В с н т ц е л ь , |
Л.А.Овчаров. - М.гРадио и связь, 1983. |
|
4 Вентцель Е.С. Теория вероятностей и её инженерные приложения /1:.С.Вентцель, Л.А.Овчаров. - М.:Наука, 1988.
5.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высшая школа, 1975.
6.Гнеденко Б.Н. Курс теории вероятностей. - М.:Наука, 1988.
7.Ежов И.И. Элементы комбинаторики /И.И. Ежов, А.В. Скороход, М.И. Ядрен к о - М . : Наука, 1977.
8.Жевержеев В.Ф. Специальный курс высшей математики для втузов /В.Ф.Жсвержеев. Л.А.Кальницкий, Н.А.Сапогов. - М . : Высшая школа, 1970.
9.Мешолкин Л.Д. Сборник задач но теории вероятностей. - М.: Изд-во МГУ. 1963.
10.Мостеллер Ф. Вероятность / Ф. Мостеллер, Р. Рурке, Дж. Томас. - М.: Мир,
1969.
11.Мостелчер Ф. Пятьдесят занимательных вероятностных задач с решениями. - М: Наука, 1971.
12.Сборник задач по математике для втузов. Специальные курсы / Э.А. Вуколов, А.В.Ефимов, В.II. Земское и др.; Под ред. А.В. Ефимова. - М.: Наука, 1984.
13.Сборник задач по теории вероятностей, математической статистике и теории случайных функций/ Б.Г. Володин, М.Н.Ганин, И.Н. Динер и др.; Под ред. А.А.Свешникова. - М.: Наука.1970.
14Тернер Д. Вероятность, статисгика и исследование операций. - М.: Статистика,
1976.
15.Феллер В. Введение в теорию вероятностей и ее приложения. - М.: Мир, 1984. -
Т.1.
Приложение
|
|
|
|
|
X |
|
|
|
|
Таблица значений функции Ф(х) = ~ \е~ |
* dz |
|
|||||
|
|
|
|
|
ы2п • |
|
|
|
|
|
|
|
|
|
|
|
|
X |
Ф(х) |
|
|
|
|
|
|
|
0.00 |
0,0000 |
0.45 |
0,1736 |
0,90 |
|
|
Ф(х) |
|
0,3159 |
1,35 |
0,4115 |
||||||
0,01 |
0,0040 |
0,46 |
||||||
0,1772 |
0,91 |
0,3186 |
1,36 |
|||||
0,02 |
0,0080 |
0,47 |
0.4131 |
|||||
0,1808 |
0,92 |
0,3212 |
1,37 |
|||||
0,03 |
0,0120 |
0,48 |
0,4147 |
|||||
0,1844 |
0,93 |
0,3238 |
1,38 |
|||||
0,04 |
0,0160 |
0.49 |
0,4162 |
|||||
0,1879 |
0,94 |
0,3264 |
1,39 |
|||||
0,05 |
0,0199 |
0,50 |
0,4177 |
|||||
0,1915 |
0,95 |
0,3289 |
1,40 |
|||||
0,06 |
0,0239 |
0.51 |
0,4192 |
|||||
0,1950 |
0,96 |
0,3315 |
1,41 |
|||||
0,07 |
0,0279 |
0,52 |
0,4207 |
|||||
0,1985 |
0.97 |
0,3340 |
1,42 |
|||||
0,08 |
0,0319 |
0,53 |
0.4222 |
|||||
0,2019 |
0,98 |
0,3365 |
1,43 |
|||||
0,09 |
0,0359 |
0,54 |
0,4236 |
|||||
0,2054 |
0,99 |
0,3389 |
1,44 |
|||||
0,10 |
0,0398 |
0,55 |
0,4251 |
|||||
0,2088 |
1.00 |
0,3413 |
1,45 |
|||||
0,11 |
0,0438 |
0,56 |
0,4265 |
|||||
0,2123 |
1.01 |
0,3438 |
1.46 |
0.4279 |
||||
0,12 |
0,0478 |
0,57 |
||||||
0,2157 |
1,02 |
0.3461 |
1,47 |
0,4292 |
||||
0,13 |
0,0517 |
0,58 |
0,2190 |
|||||
1,03 |
0,3485 |
1,48 |
0,4306 |
|||||
0,14 |
0,0557 |
0,59 |
0,2224 |
|||||
1.04 |
0,3508 |
1,49 |
0,4319 |
|||||
0,15 |
0,0596 |
0,60 |
0,2257 |
|||||
1,05 |
0,3531 |
1,50 |
0,4332 |
|||||
0,16 |
0,0636 |
0,61 |
0,2291 |
|||||
1.06 |
0,3554 |
1,51 |
0,4345 |
|||||
0,17 |
0,0675 |
0,62 |
0,2324 |
|||||
1,07 |
0,3577 |
1,52 |
0,4357 |
|||||
0,18 |
0,0714 |
0,63 |
0,2357 |
|||||
1,08 |
0,3599 |
1,53 |
0,4370 |
|||||
0,19 |
0,0753 |
0.64 |
||||||
0,2389 |
1,09 |
0,3621 |
1,54 |
0,4382 |
||||
0,20 |
0,0793 |
0,65 |
||||||
0,2422 |
1,10 |
0,3643 |
1,55 |
0.4394 |
||||
0,21 |
0,0832 |
0,66 |
||||||
0,2454 |
1,11 |
0,3665 |
1.56 |
0,4406 |
||||
0,22 |
0,0871 |
0,67 |
0,2486 |
|||||
1,12 |
0,3686 |
1,57 |
0.4418 |
|||||
0,23 |
0,0910 |
0,68 |
0,2517 |
|||||
1,13 |
0,3708 |
1,58 |
0,4429 |
|||||
0.24 |
0,0948 |
|||||||
0,69 |
0,2549 |
1,14 |
0.3729 |
1,59 |
0,4441 |
|||
0,25 |
0,0987 |
|||||||
0.70 |
0.2580 |
1,15 |
0,3749 |
1,60 |
0,4452 |
|||
0,26 |
0,1026 |
0.71 |
0,2611 |
|||||
1,16 |
0,3770 |
1,61 |
0,4463 |
|||||
0,27 |
0,1064 |
0,72 |
0,2642 |
|||||
1,17 |
0,3790 |
1.62 |
0,4474 |
|||||
0,28 |
0.1103 |
0,73 |
0,2673 |
|||||
1,18 |
0,3810 |
1,63 |
0,4484 |
|||||
0,29 |
0,1141 |
0,74 |
0,2703 |
|||||
1,19 |
0,3830 |
1,64 |
0,4495 |
|||||
0.30 |
0,1179 |
0,75 |
||||||
0,2734 |
1,20 |
0,3849 |
1,65 |
0,4505 |
||||
0,31 |
0,1217 |
0,76 |
||||||
0,2764 |
1,21 |
0,3869 |
1,66 |
0,4515 |
||||
0.32 |
0,1255 |
0,77 |
||||||
0,2794 |
1,22 |
0,3883 |
1,67 |
0,4525 |
||||
0,33 |
0,1293 |
0,78 |
0,2823 |
|||||
1,23 |
0.3907 |
1,68 |
0,4535 |
|||||
0,34 |
0,1331 |
|||||||
0,79 |
0,2852 |
1,24 |
0,3925 |
1,69 |
0,4545 |
|||
0,35 |
0,1368 |
0,80 |
||||||
0,2881 |
1,25 |
0,3944 |
1,70 |
0,4554 |
||||
0,36 |
0,1406 |
0,81 |
||||||
0,2910 |
1,26 |
0,3962 |
1,71 |
0,4564 |
||||
0,37 |
0,1443 |
0,82 |
||||||
0,2939 |
1,27 |
0,3980 |
1.72 |
0,4573 |
||||
|
|
|
|
|||||
