
1282
.pdf
Вычислим математические ожидание левой и правой частей. 1 получим формулу, по которой подсчитывается дисперсия суммы случайных величин:
D(Sn) = M(Sn |
-Мп)2= |
|
|
+ 2 I C o v ( ^ , X ; ) . |
(9.11) |
||||
|
|
|
|
|
1 |
|
i,j>i |
|
|
Последняя |
сумма |
состоит из |
С\чисел |
Cov(XhX j),причем i <j. |
|||||
Если случайные величины Х„ Х} попарно независимы, получается у; |
|||||||||
доказанная формула |
|
|
|
|
|
||||
D{Sn) |
|
|
= |
|
M{Sn-Mn)2=tDiXiy |
|
|
||
9.5. |
|
Коэффициент |
корреляции |
|
|
||||
Пусть |
X |
и |
Y |
- |
две |
случайные величины |
|
||
ожиданиями М(Х) |
и |
M{Y) и дисперсиями 0{Х) и IXX)- |
|
||||||
Коэффициентом |
корреляции |
случайных |
величин Ми |
Y(обозначается |
|||||
через р(Х, |
Y)) называется ковариация нормированных случайных величин |
||||||||
Хи Y. |
|
|
|
|
|
|
|
|
|
р(Х, Y) = Cov(M, Y) = Соу(МУ)/(СТ, |
|
|
|||||||
Если X и Y независимы, то р(Х, |
Y) = 0. |
|
|
||||||
Обратное утверждение неверно. Коэффициент корреляции может быЛ равен нулю, но Y является функцией X.
Пример. Величина Л" принимает значения: ±1и ± 2 с вероятностям! 0,25 каждое. Тогда М(Х) = 0. Положим Y - X2. Закон распределения ХМ
таков: |
|
|
|
• |
|
|
|
-8 |
-1 |
1 |
8 |
|
Р |
1/4 |
1/4 |
1/4 |
1/4 |
|
|
|
|
|
|
Докажем, что всегда \р(Х, У)| < 1, причем равенство р{Х, Y) = справедливо тогда и только тогда, когда случайные величины X и
связаны линейной зависимостью. |
|
|
|
|
Действительно, |
|
|
|
|
D(X±Y) = DiX)±2Cov(X, |
Y) + D(Y) = 2[l |
± p(X, Y)\ |
Так |
как диспер |
всегда неотрицательна, то |
|
|
|
|
1 ± Я ( Х , У ) > 0 = > | р ( М , У)|<1. |
|
|
|
|
Пусть \р{Х, Y)\ • 1. |
Значит, либо |
D(X + Я) = 0, |
либо |
D(X - Y) = 0. |
равна нулю только дисперсия константы, поэтому
|
|
|
|
|
|
|
I |
|
|
M±P = const=>r = C± — X. |
|
|
|
|
|
||||
Если |
же |
Y = аХ + b, |
то |
M(Y) = |
аЩХ) + |
Ь\ |
D(Y) = a2D(X); |
||
M(XY) |
= |
аМ(Х2) |
+ |
ЬМ(Х); |
|
M(X)M(Y) = |
аМ2(X) |
+ |
ЬЩХ)\ |
Cov(X, |
Y) |
= |
aD(X); |
|
|
|
|
|
|
p/v У) = - |
^ X L = j 1 ' |
если a > 0; |
|
|
|
|
|||
|
|a|crxcr;r |
[-1, |
если |
a < 0. |
|
|
|
|
|
9.6. |
|
Примеры |
решения |
задач |
|
|
|
|
|
9.6.1. Определить математическое ожидание и дисперсию случайной величины X, имеющей биномиальное распределение.
Решение. Случайная величина X - число появлений "успеха" в п независимых испытаниях - есть сумма п независимых случайных величин,
X = Х{ + Х2 |
+ ... + Хп> где Xi - число появлений "успеха" в /-м испытании, |
||||
/ = 1, 2, |
п. Но закон распределения величины |
X, |
очень прост, это |
||
множество |
{(0, q), |
(1, р)}. Отсюда ЩХ) = 0q+\-p= |
р\ |
ЩХ2)= |
ЩХ,) - /г, |
/ НЛ,) = /? - р 2 = pq. |
Поэтому |
|
|
|
|
М ( Х ) = % Щ Х |
, ) = np; D i X ) = £ D(M( ) = npq; |
a ( X ) = |
Jnp~q~. |
||
|
i |
l |
|
|
|
9.6.2. Сколько игральных кубиков надо бросить, чтобы математическое ожидание числа кубиков, на которых выпало одно очко, равнялось 5?
Решение. Пусть брошено п кубиков. Число кубиков, на которых выпало одно очко, - биномиально распределенная случайная величина X с пара метрами пнр = 1/6, М(Х) = л/6. По условию л/6=5, тогда п = 30.
9.6.3. Считая, что вес тела с равной вероятностью может быть равен любому целому числу граммов от 1 до 10, определить, при какой из трех систем разновесов: а) 1;2; 2; 5; 10; б) 1; 2; 3; 4; 10; в) 1; 1; 2; 5; 10-среднее число необходимых для взвешивания гирь будет наименьшим, если при взвешивании гири разрешается ставить только на одну чашку и каждый РАЗ нужно использовать минимально возможное число гирь. Определить I лкже, в каком из трех случаев минимален средний разброс относительно среднего числа требуемых гирь.
Решение. Составим законы распределения трех случайных величин X, У, Z- количества гирь, нужных для взвешивания в каждом из трех случаев, (начала в каждой таблице оставим по 10 столбцов (/-й столбец 'ответствует весу тела, равному / граммов). Потом объединим столбцы, в которых стоят одинаковые значения случайной величины (табл. 9.3 - 9.8).
82 |
83 |

Поясним переход от табл. 9.3 к табл. 9.4. Случайная величина X принимает значение 1 . если вес тела равен 1г, или 2 г, или 5 г, или Юг. Это событие есть сумма четырех несовместных событий, поэтому его вероятность равна сумме вероятностей каждого из событий-слагаемых, т.е. равна 0,1 + 0,1 + 0,1 + 0,1 = 0,4. Подобным образом находятся вероятности
событий |
{Х= 2} и |
{Х= 3} |
(0,4 и 0,2 соответственно). |
|
|
|
Таблица 9.3 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 9.3 |
|
|||
|
|
|
|
|
1 |
|
1 |
|
|
2 |
2 |
|
|
|
1 |
|
|
2 |
|
|
|
|
2 |
|
|
3 |
|
3 |
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
й |
0,1 |
|
|
од |
0,1 |
0,1 |
|
|
|
|
од |
|
0,1 |
|
|
|
|
0,1 |
|
|
0,1 |
|
0,1 |
0,1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Окончательная таблица: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 9.4 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pi |
|
0,4 |
|
0,4 |
|
0,2 |
|
|
|
|
|
|
Таблица 9.5 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
v.- |
|
1 |
|
1 |
|
|
1 |
1 |
|
|
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
3 |
|
3 |
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
. / ' . . . |
|
0,1 |
|
0,1 |
|
|
0,1 |
0,1 |
|
|
0,1 |
|
0,1 |
|
|
|
|
0,1 |
|
|
0,1 |
|
0,1 |
0,1 |
|
|
||||||||||||
|
|
Pi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Окончательная таблица: |
|
|
|
|
|
|
Таблица 9.6 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У! |
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
—Ж. |
0,5 |
|
0,3 |
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pi |
|
|
|
|
|
|
|
Таблица 9.7 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Z. |
1 |
|
|
1 |
|
|
2 |
— з — 1 |
1 |
|
|
2 |
|
|
|
|
2 |
|
|
3 |
|
4 |
|
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
0,1 |
|
|
|
0,1 |
|
0,1 |
|
0,1 |
|
0,1 |
|
|
|||||||||||||||||||
|
|
Pi |
од |
|
0,1 |
|
|
0,1 |
0,1 |
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
Окончательная таблица: |
|
|
|
|
|
|
|
|
|
Таблица 9.8 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Pi |
|
0,4 |
|
|
0,3 |
|
|
|
0,2 |
|
|
0,1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем математические ожидания и дисперсии каждой из случайных |
|||||||||||||||||||||||||||||||||||||
|
величин. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Л/(ЛГ) = 1-0,4 + 2 - 0 , 4 + 3-0,2 = 1,8; D(X) = l2 |
• 0,4 + 22 |
|
• 0,4 + З2 |
0,2 = 0,56; |
||||||||||||||||||||||||||||||||||
|
ст(Х) = ЩХ) = 0,748; M(Y) = 1 • 0,5 + 2 • 0,3 + 3 • 0,2 = 1,7; |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
Д У ) = 12 |
0,5 + 22 |
0.3 + 32 |
|
-0,2 = 0,61; cr(Y) = JD{Y) = 0,781; |
|
|
|
|
||||||||||||||||||||||||||||||
|
M(Z) = 1 • 0,4 + 2 • 0,3 + 3 • 0,2 + 4 • 0,1 = 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
D(Z) = 12 |
-0,4 + 22 |
-0.3 + 32 |
-0,2 + 42 -0,1-22 |
=1; |
|
<j(Z) = J5(Z) = 1. |
||||||||||||||||||||||||||||||||
В среднем наименьшее число гирь требуется для второго набора разновесов. А наименьшее среднее отклонение от математического ожидания числа гирь (0,748 гири) получилось для первого набора.
9.6.4. Корректура в 500 страниц содержит в среднем 1300 опечаток. Считая применимым закон Пуассона, найти наиболее вероятное число опечаток на одной странице и вероятность этого числа.
Решение. Условие задачи нужно понимать так: случайная величина А"- количество опечаток на некоторой странице текста - распределена по закону Пуассона с параметром Я - средним числом опечаток на странице. Значение параметра одинаково для всех страниц, поэтому среднее число опечаток на пятистах страницах равно произведению 500Я. Нужно приравнять 500Я числу 1300, откуда Я = 2,6.
Вычислим вероятности событийр(Х = 0),р(Х= 1),....
р(А- = 0 ) = ^ |
— = 0,074 |
;р(АГ = 1 ) = ^ - ^ = 0,193; |
р(Х = 2) = - |
^ — = 0,251; |
р(Х = 3) = —^— = 0,218. |
Ясно, что следующие вероятности будут только убывать, поэтому наиболее вероятное число опечаток на одной странице (мода случайной величины X) равно 2, вероятность этого числа равна 0,251.
9.6.5. Доказать, что дисперсия случайной величины X - числа появлений события в одном испытании - не превосходит 0,25.
Решение. Пусть вероятность появления события в одном испытании
равна р, тогда вероятность непоявления события равна |
1 -р |
= q. В задаче |
||
9.6.1 |
была найдена дисперсия случайной величины X, |
D(X) |
= р(\ - р), при |
|
лом |
0 < р <, 1. Найдем максимум ЩХ) |
как функции р на отрезке [0,1]. |
||
D'(p)-l ~2р- Приравнивая производную |
нулю, получаем, |
что р = 0,5. |
||
Легко убедиться, что при р = 0,5 достигается именно максимум дисперсии, он равен числу 0,52 = 0,25.
9.6.6. Сколько изюма должна содержать в среднем булочка, чтобы вероятность иметь хотя бы одну изюминку в булочке была не менее чем 0.99?
Решение. Испытание здесь - проверка, попала ли данная изюминка в данную булочку. Испытания предполагаются независимыми; количество изюминок исчисляется тысячами; вероятность "успеха" ничтожно мала. 11оэтому число X изюминок в булочке можно считать случайной величиной, имеющей распределение Пуассона. Так как М(Х) = Я, нужно определить значение параметра Я. Из условия р(Х> 1) > 0,99 получаем, что
Я0 • е~х р(Х=Щ\ -р(Х> 1)^0,01. С другой стороны, р(Х = 0) = — ' - — = е~я.
Итак, е~л < 0,01, отсюда -Я < -4,605 => Я > 4,605. Булочки должны содержать в "среднем" по 5 изюминок.
84 |
85 |
|

9.6.7. Найти математическое ожидание и дисперсию случайной величины X, имеющей геометрическое распределение, начинающееся с единицы.
|
|
|
1 |
|
|
|
2 |
|
|
3 |
|
|
|
|
к |
|
|
|
|
|
|
Pi |
|
р |
|
|
|
ЯР |
|
|
ft |
|
|
|
|
|
|
|
... |
|
|
|
|
Тогда |
В Д |
= 1 Ь Г Р = Р Й к-\ |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
] |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Легко доказать, |
что |
ряд |
^kqk 1 сходится. Произведение |
какЛ |
есть |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
производная функции qk по д. Отсюда |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
_ 1 ^ Д / ( М ) = - , |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
О-?)2 |
|
|
|
||||
|
I |
|
|
|
|
|
|
|
|
1 - 9 |
|
|
Р2 |
Р |
|
|
||||
ведь X*?* - это сУмма геометрической прогрессии со знаменателем q |
< 1. |
|||||||||||||||||||
Далее, |
М(Х2) = £ * У |
|
Р = Р^к.22д_*-1 |
Ряд |
1 * 4 |
|
|
СХОДИТСЯ, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
||
k~q |
= — kq , |
поэтому |
|
|
|
|
|
|
|
|
|
|
|
|||||||
7 * 4 |
вЕ-^*г |
=-гяУкя |
=-—1—г= |
|
г = — г |
|
|
|||||||||||||
7 |
|
|
|
|
|
</<? . |
|
<*Г(1-?)2 |
|
о - * ) 3 Р3 |
|
|
|
|||||||
|
Отсюда |
Л/(ЛГ2) = - ^ ; |
|
1 + а |
1 _ |
q |
|
|
|
|||||||||||
|
|
|
|
|
.2 ' |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Следовательно, случайная величина У = X -- 1,1, которая имеет! геометрическое распределение, начинающееся с нуля, обладает такими характеристиками: M(Y) = М(Х-1) = М(Х)-\ = qlр;
D(Y) = D(X-\)=D(X) = q/p2; cr(Y) = 4q~lp.
9.6.8. Для привлечения покупателей некоторые фирмы вкладывают в • коробки со своим товаром (жевательная резинка, конфеты и т.п.) купоны, занумерованные цифрами от 1 до 5 (по одному купону в коробке). Покупатель, набравший полный комплект из 5 купонов с разными { номерами, получает одну коробку бесплатно. Сколько коробок в среднем надо купить, чтобы получить полный комплект купонов?
Решение. Случайная величина X - число купленных коробок до, получения полного набора купонов - есть сумма 1 + Х\ + Х2 + Х3 + где Х\ - это число купленных коробок до получения номера, не совпадающего с номером в первой коробке, Х2 - число купленных коробок
до получения номера, не совпадающего с полученными двумя первыми и г.д. Составим закон распределения случайной величины Х\.
Вероятность того, что сразу попадется коробка, номер которой не совпадает с первым, равна 4/5. Вероятность того, что такая коробка будет
1 4 приобретена со второй попытки, равна ——. Вероятность удачи с третьей
1 1 4 попытки равна произведению — • —
(\ V"1 |
4 |
Таким образом, р(Хх =к)= — |
—. Получилось геометрическое |
^5) |
5 |
распределение, начинающееся с единицы, его параметры Р\ =4/5 и q\ =1/5.
Значит, М(М,)= 1 =5/4 . |
|
|
|
|
|
Р\ |
|
|
|
Аналогично |
случайная |
величина Х2 |
имеет |
геометрическое |
распределение, |
начинающееся с 1, с параметрами р2 |
=3/5 и q2 =2/5, |
||
\f(X2) = — = |
5/3. |
|
|
|
Pi |
|
|
|
|
Далее случайные величины Х3 и Х4 имеют геометрическое распределение, начинающееся с 1, причем р3 =2/5, р4 =1/5. Тогда М(Х3) = 5/2, М(ХА) = 5. Следовательно, М(Х) = 1 + 5 / 4 +5/3 + 5/2 + 5 * 11,42 .
Всреднем потребуется купить 11,42 коробок.
9.6.9.Восемь девушек и семь юношей независимо приобрели по одному билету в одном и том же театральном ряду, насчитывающем 15 мест. Каково среднее число образовавшихся пар?
Решение. Пусть X - это случайная величина, равная числу пар. Если, например, юноши и девушки расселись в таком порядке: ЮДДДЮЮДЮДЮДЮДДЮ, то число пар равно 10.
Случайная величина X есть сумма 14 случайных величин (вообще
14
говоря, зависимых), X = ^Хк, где Хк - число пар на местах с номерами
1
к и я+1, к = 1,2,..., 14. Случайная величина Хк принимает только два шачения - 0 или 1; Хк = 0, если билеты с номерами к и к+1 приобрели двое юношей или две девушки; в противном случае Хк = 1. Найдем вероятности значений величины Хк.
р(Хк = 0) |
= ^ . A |
+ 1 . 1 = Z ; |
р{Хк |
= 1 ) |
= 1 - ! = ! ; |
|||||
|
15 |
14 |
15 |
14 |
15 |
|
|
15 |
15 |
|
М(Хк)=\— + 0— |
= |
—; |
М(Х) |
= |
\4— |
«7,5. |
|
|||
* |
15 |
|
15 |
|
15 |
|
|
15 |
|
|
86 |
S7 |
9.6.10. Из хорошо перетасованной колоды в 52 карты, содержащей туза, извлекаются сверху карты до появления первого туза. На каком м в среднем появится первый туз?
Решение. Перенумеруем места в колоде числами от 1 до 52. Тог. элементарный исход - это упорядоченная четверка чисел (пх, п2, пъ, и4 номеров мест тузов (1 < и, < п2 < и3 < п4 < 52). Например, исход (5, 9, 1 35) означает, что тузы занимают пятое, девятое, десятое и тридцать п места. Исходы равновозможны, всего их С\2. Но эти же элементар исходы можно задать и по-другому. Каждому набору номеров ту соответствует упорядоченный набор из пяти чисел - длин пяти ча колоды, на которые четыре туза ее делят.
Например, исходу (5, 9, 10, 35) соответствует пятерка (4, 3, 0, 24, 17).
общем случае |
исходу (л,, |
п2, л3 , пл) |
соответствует |
упорядоченн |
||||
пятерка чисел |
(х,, х2, х3, х4, |
х 5 ), где х, |
= пх |
- 1 ; х2 =п2 |
- л , - 1 |
; |
х3 »1 |
|
= л3 - л 2 |
- 1 ; х4 = л4 - л 3 - 1 ; х5 = 5 2 - л 4 - 1 , |
х,,х 2 ,х 3 ,х 4 ,х 5 £ 0 , |
|
хх |
||||
+ х2 + х3 |
+ х4 + х5 = 48. |
|
|
|
|
|
|
|
При таком описании исходов становится понятно, что все события At = {/-я часть колоды содержит к карт, / =1, 2, 3, 4, 5} состоят из одного того же числа исходов, ведь между исходами можно установить взаим-
однозначное соответствие. |
Например, |
пятерке |
(к, х2, х3, х4, х |
||||
ставятся |
в соответствие |
наборы (х2, к, х3, х4, х5 ), (х3, |
х2, к, |
х4, х5 |
|||
(х4, х2, х3, к, х5 ), (х5, х2, х3, х4, к). |
|
|
|
|
|||
Из этих рассуждений вытекает совпадение законов распределе |
|||||||
случайных величин Хх, Х2, Х2, Х4, Х5- |
длин кусков каждой из п |
||||||
частей |
колоды. Так |
как |
сумма этих |
величин |
равна |
числу |
48, |
М{ХХ) = М{Х2) = ••• = М(Х5) = 4Ъ/5 = 9,6. |
Тогда в |
среднем первый |
|||||
должен быть 9,6 -+-1 = 10,6 картой.
Профессиональный математик изложил бы решение этой зада гораздо короче. Он рассуждал бы примерно так. Четыре туза делят коло на 5 частей. Из соображений симметрии следует, что средние дли каждой из частей одинаковы. Значит, средняя длина каждой части равн 48/5 = 9,6. Тогда в среднем первый туз должен быть 9,6 + 1 = 10,6 картой^ За одной короткой фразой профессионала может скрываться весьмв) длинное рассуждение, совсем не очевидное для того, кто только начинает изучать данную дисциплину.
9.6.11. Пусть Х\, Х2, .... Хп Х„,\ - это последовательность попарно независимых и одинаково распределенных случайных величин^ принимающих с вероятностью р значение 1 и вероятностью q =1 - р
шачение 0. Положим У, = 0, если Х+ Хщ=0 или 2; У, = 1, если Х+ Х,.х = 1. 11айти математическое ожидание и дисперсию суммы У, + У2 + ... + Y„.
Решение. Составим закон распределения случайной величины У,.
рХГ, = 1) = р(Х, = 0, Xi+] = 1) + p(Xi = 1, Хм = 0) = 2pq; p(Yi=0) = \-2pq.
Представим закон распределения величины У, в табл. 9.9.
|
|
|
|
|
|
|
Таблица 9.9 |
|
|
У, |
|
0 |
|
|
1 |
|
|
|
Р\ |
|
\-2pq |
|
|
2pq |
|
|
Здесь /- 1, 2, |
|
|
|
|
|
|
|
|
п. |
|
|
|
|
|
|
|
|
Определим числовые характеристики случайной величины У,. |
||||||||
M{Yi) = 2pq; |
M(Yl2) = 2pq; |
D{Y,) |
= 2pq-4p2q2 = 2pq(l - 2pq). |
|||||
Вычислим Cov(y,, Yk). |
|
Для |
этого |
составим закон распределения |
||||
произведения Y{YK где i < к. Рассмотрим два случая:
а) к > i + 1. В этом случае У, и У,., независимы, Cov(Yit Yk). = 0.
б) к = i + 1. Произведение У, У,_, принимает значение 1, когда либо одновременно X, =1, ХМ = 0, ХМ = 1, либо одновременно X, =0, Х,.х = 1, Xi-i = 0. Вероятность первого события равна произведению p2q, вероятность второго равна числу q2p. Тогда
PV&JTI = 1) = Л + Я2Р = РЧ\ |
|
=0) = \-pq. |
|
|
|||||||||
Закон распределения произведения У, У,+1 представлен в табл. 9.10. |
|||||||||||||
|
|
|
|
|
|
|
|
|
Таблица 9.10 |
|
|
||
|
|
|
ЦК* |
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
Р' |
|
1 |
-pq |
|
РЧ |
|
|
|
|
|
Значит, Л/(У,У,+ 1) - pq; |
Соу(У„ |
Yi+]) = pq4p2q2 |
= pq(\ - |
4pq). Тогда |
|||||||||
|
|
|
I |
1 |
|
|
|
|
|
|
|
|
|
+ (n-l)-2pq(\-4pq) |
= 2pq[n(l-2pq) + |
(n-\)(p-q)2], |
так |
как |
разность |
||||||||
(1 - 4pq) можно представить в виде |
|
|
|
|
|
|
|
|
|||||
1 |
-4pq = |
\-4pa-p) = |
|
\-4p |
+ |
4p2 |
=(l-2p)2 |
=(q-p)2 |
=(p-q)2. |
||||
8S
1 0 . П О Н Я Т И Е О Н Е П Р Е Р Ы В Н Ы Х С Л У Ч А Й Н Ы Х В Е Л И Ч И Н А Х
10.1. |
Определение |
непрерывной |
случайной |
величины. |
|
Функция |
распределения |
и |
функция |
плотности |
|
вероятности |
непрерывной |
|
случайной |
величины |
|
Дискретная случайная величина - это числовая функция, область определения которой есть конечное или счетное множество элементарных исходов. Множество ее значений также конечно или счетно. Но счетное множество элементарных исходов - лишь небольшой частный случай пространства Q. Даже если отвлечься от теоретических рассуждений и обратиться к практическим задачам, несчетные множества сразу заявят о себе. Вот пример из поистине безграничного числа возможных.
Фирма, выпускающая автомобильные двигатели, разработала новую модель. Фирма хотела бы установить такой гарантийный срок работы этой модели, чтобы, с одной стороны, заинтересовать клиентов, но, с другой - не разориться из-за большого числа бесплатных ремонтов. Кроме тогол фирма хотела бы оценить процент двигателей, которые выйдут из строя в пределах гарантийного срока (чтобы оценить, таким образом, возможные финансовые потери), и процент двигателей, которые проработают не менее] двух гарантийных сроков (чтобы использовать эти данные в рекламных^ целях). Здесь случайная величина Т - время работы двигателя до первой' поломки - во всяком случае не дискретна. С некоторыми отступлениями oti истины множество ее значений можно соотнести с интервалом (0, ос), «• множество точек отрезка несчетно. Ниже будут рассмотрены так называемые непрерывные случайные величины (снова только частный случай общего понятия), множества значений которых заполняют целиком один или несколько интервалов числовой оси (или распространяются на; всю числовую ось).
Пусть имеется несчетное пространство элементарных исходов Q и на' его основе задано вероятностное пространство, причем множество событий образует сг-алгебру. Зададим на множестве Q числовую функцию (случайную величину) X, которая каждому элементарному исходу со ставит
в соответствие число |
х(со) - значение случайной величины X, так |
что |
Vx е (-ос, оо)событие А |
• {Х<х} входит в алгебру событий, тем самым |
для |
события А определена вероятностьр(А). Вместе с каждым событием {АЧх}|
в сг-алгебру событий |
входит |
также |
противоположное |
событие |
||
A={XZx). |
Из |
равенства |
{хх |
<.Х <х2} = {Х <х2}\{Х <хх}, |
х2>М |
|
следует, |
что |
событие |
{хх<Х<х2} |
также |
принадлежит о--алгебре |
|
событий.
Покажем, что всякое событие вида {X = х0} тоже входит в ст- алгебру
событий. Справедливость этого утверждения следует из равенства
ЕЕ
{X |
= х0} = f]{x0 |
<X<х0 +1/п}. |
Следовательно, |
а -алгебре |
событий |
|||
принадлежат |
и |
все |
события |
вида {Х<х0}; |
{X > х0); |
{хх |
<> X <>х2}; |
|
{*, |
<Х<.х2)\{хх |
<Х<х2). |
|
|
|
|
||
|
Одновременно задается функция распределения случайной величины |
|||||||
|
F(x) = р(Х < х), |
-сс<х<ао. |
|
|
|
( ю . | ) |
||
|
Случайную |
величину X будем называть непрерывной, |
если функция |
|||||
F(x) дифференцируема (следовательно, F(x) непрерывна) и ее производная
dF |
|
|
|
|
|
|
|
|
— = / ( * ) , |
- ° о < х < о о |
|
|
|
|
(Ю.2) |
||
является^ кусочно-непрерывной |
функцией. |
Функция |
fix) |
называется |
||||
функцией плотности вероятности случайной величины X. Перечислим |
||||||||
некоторые свойства функций |
F(x) |
nj(x). |
|
|
|
|||
1. |
0 < F{x) < |
1. |
|
|
|
|
|
|
2. |
Еслих 2 >х,,то F(x2) |
= p(X <хх) + р(хх |
< X < х2)> р(Х |
< хх) = |
||||
= Fixx) => Fix) - неубывающая функция. |
|
|
|
|||||
3. |
р(хх |
<>X<x2) = Fix2)-Fixx). |
|
|
|
|||
4. F(-oo) = р(Х < -со) = 0; |
F(+co) = р(Х < +со) = 1. |
|
||||||
5. |
р(Х = х0)= |
lim pix0 |
<,Х <xQ+ Ах) = lim ( F ( * 0 |
+ Дх) - F(x0 )) = |
||||
|
|
|
Л*->0 |
|
|
Дг-+0 |
|
|
= hm^ ДхуТхо)=0, для любого х0 е (-co.ee). |
|
|
|
|||||
Таким образом, вероятность любого элементарного исхода со равна
нулю.
6. р(хх < X < х2) = р{хх <, X < х2) = р(хх < X < х2) = р(хх < X <х2) =
=F(x2)-Fixx), так как
р(хх |
£ X |
<x2) = piX = xx)+pixx |
<Х<х2) |
=piX |
= xx) + p(X = x2) + |
• |
р(хх |
<Х<х2) = р(Х = |
х2) + |
р(хх |
<X<x2)=Fix2)-F(xx),(x2>xl). |
Итак, если X - непрерывная случайная величина, то равна нулю вероятность любого события вида {"случайная величина X приняла шачениехо"}, отличными от нуля могут быть только вероятности событий
вида |
{"случайная величина X приняла значение из интервала (а, Ь), |
-х |
<а,Ь<со"}. |
7.По формуле Ньютона - Лейбница
ь |
|
pia<X<b) = Fib)-Fia)=\f{x)dx, |
- с о < а , 6 < о о . |
90
Соглашение о кусочной непрерывности функции J[x) гарантируе существование интеграла.
8. Производная неубывающей функции неотрицательна, fix) > 0. Если для некоторого числа х0 значение Дх0) = 0, то говорят, чк&
случайная величина X не принимает значения х0; если же Дх0) > 0, то говорят, что случайная величина X может принять значение х{). Ит кусочной непрерывности J{x) вытекает, что множество значений, которые может принимать непрерывная случайная величина, либо целиком заполняет числовую ось, либо состоит из одного или нескольких непересекающихся интервалов.
9. |
р{Х < оо) = р(-со < X < о о ) = | / ( x ) d x = 1, ведь событие |
{X < ос§ |
является достоверным событием. |
|
|
|
х |
|
10. |
F(x) = pi-ao <Х<х)= \ f { t ) d t . |
(10.3)| |
—СО
Этот интеграл - есть функция своего верхнего предела х, поэтом* подынторальная переменная обозначена другой буквой.
Будем говорить, что непрерывная случайная величина X задана (или задан закон распределения непрерывной случайной величины X), если определена одна из двух функций - функция распределения F(x) или функция плотности вероятности у(х). Зная одну из этих функций, можно определить другую (см. формулы (10.2), (10.3)).
Внимательный читатель не может не заметить некоторого! несоответствия в высказываниях о событиях вида {Х = х 0 } , где X- непрерывная случайная величина. Действительно, с одной стороны, вероятность события {Х=х0} равна нулю, а невозможные события не могут произойти. С другой стороны, мы утверждали, что случайная величина X может принять значение х0, если _Дх0) > 0. Подобное противоречие можно разрешить, используя, например, методц нестандартного анализа. Тогда можно приписать событию {" непрерывная случайная величина X приняла значение из интервала dx бесконечно
малой длины"} бесконечно малую, но отличную от нуля |
вероятность dp. |
Но интервал бесконечно малой длины содержит |
только одно |
действительное (стандартное) число. Событие {X = х0) перестает быть невозможным, у него появляется бесконечно малая, но все-таки отличная от нуля вероятность.
В рамках данного учебного пособия мы ограничимся следующим заявлением. В случае непрерывной случайной величины рассчитать вероятность можно только для событий, подобных событию
{*, < X < х 2 } , х 2 > х , . Вероятность события {Х = х0} неотличима от •уля, но утверждение "случайная величина X может принять значение х0, гели У(х0) > 0" корректно в том смысле, что X может принять любое значение из некоторого интервала, содержащего число х0, в том числе и само значение х0.
10.2. Примеры решения задач
10.2.1. Непрерывная случайная величина X задана функцией плотности вероятности f(x) = ! , 5 s i n 3 x B интервале (0, яг/3). Вне интервала/(х) = 0. Чайти функцию распределения F(x) случайной величины X и вероятность то, что в трех независимых испытаниях величина X ровно два раза
римет значение из интервала (0, ж/4). Решение.
X X
1. Пусть х <, 0, тогда F(x) = \ f { t ) d t = J o • dt = 0.
оо
2. |
Пусть 0 < х < 7г/3. Тогда |
|
|
|||
|
|
х |
о |
х |
|
|
|
= |
J /(0*7 |
= |
J0-dt+ |
Jl,5sin2tdt = |
0,5(1 -cos3x). |
|
|
-co |
-co |
0 |
|
|
3. |
Пусть x > ж/3. Тогда |
|
|
|||
|
|
x |
0 |
я 7 3 |
дг |
|
F(x) = |
J /(0*7 = |
|
\0-dt+ |
J l,5sin3/*7 + |
JO• dt = 1. |
|
|
|
-оо |
-oo |
0 |
zr/3 |
|
Окончательно |
|
|
|
|
||
|
|
|
|
0, если x < 0; |
|
|
|
|
F(x) = |
0,5(1 - cos Зх); если 0 < x < n 13; |
|||
1, еслих>/г/3.
Определим вероятность попадания случайной величины X в интервал
10, ж/4).
p(0<x<7t/4) = F(nl4)-F(0) = 0,5 (1 - cos —) = 0,854. 4
Вероятность того, что в трех независимых испытаниях величина X ровно два раза примет значение из интервала (0, ж/4), находим по формуле Ьернулли
р3(2) = С\ • 0,8542 • (1 - 0,854)' = 0,32.
10.2.2. Случайная величина А'имеет такую плотность вероятности:
92 |
93 |
|
ГО, если х < 1;
f(x) = \ |
2 |
[А/х |
, е с л и х > 1 . |
Требуется найти коэффициент А и F(x). Решение. Число А находим из условия
ОО |
00 |
jf(x)dx = |
\=> \Alx2dx = \, тогда |
I1
=1=> А = 1.
Когда х< 1 , t o F ( x ) = 0. Если х £ 1, то
F(x) = |
)nt)dt |
= )\dt |
= |
x |
1 |
^- |
= 1 —. Таким образом |
||||
-00 |
1 t |
* |
l |
x |
|
|
FO, если x < 1, |
|
|
|
|
F(x) = |
1 —1, если x > 1. |
|
|
||
|
x |
|
|
|
|
10.2.3. Дана некоторая функция одного аргумента О, если х < О,
0,2,если0<х<1,
F(x) = 0,1, если 1 < х < 3 ,
1,еслих > 3.
Является ли F(x) функцией распределения непрерывной случайной величины?
Решение. Функция F(x), во-первых, не является непрерывной, вовторых, не является возрастающей. Следовательно, F(x) не может быть функцией распределения непрерывной случайной величины.
10.3. |
Понятие |
о |
функции |
непрерывной |
случайной |
величины |
Пусть задана некоторая непрерывная случайная величина X и монотонная числовая функция у = <р(х) (у монотонной функции всегда есть обратная функция, тоже монотонная) такая, что ее обратная функция у = у/(х) дифференцируема. Наличие обратной функции означает, что событие {ф(Х) < х) входит в алгебру событий и, следовательно, ему приписана некоторая вероятность.
Определим случайную величину Y = <р(Х) как числовую функцию, которая каждому элементарному исходу со ставит в соответствие число,
94
равное (р(х(со)), где х(со) - значение случайной величины X на исходе со. Наша цель - определить функции распределения Fy(x) и плотности ьероятности /у{х) случайной величины Y по известным функциям распределения F(x) и плотности вероятности fix) случайной величины X.
Рассмотрим сначала два конкретных примера. Пример 1. Пусть у = х3, тогда
p(Y<х) = р(Х3 |
<х) = р(Х <Ч~х) = F(3VI); |
FY(x) = F(V7). |
||
Функция у = Vx, обратная к функции у = х3. |
|
|||
fr(x) = -^-Fy(x) = — F(Vx). По правилу дифференцирования сложной |
||||
|
dx |
dx |
|
|
функции |
|
|
|
|
dx |
dx |
d(^c) |
3 |
|
Пример 2. Рассмотрим функцию^ • -х3. Обратная функция: у = -Цх . |
||||
|
FY(х) = p\Y <Х) = р(-Х3 < х) = р(Х3 |
> -х) = р(Х>-Цх~) = |
||
|
= 1 - р(Х < -Vx) = 1 - /г(_з/^) |
|
||
|
/у (х) = ^-Fy(x) = - 4 ( 4 / 1 ) - (Я-\Гх)) = ix-2/3/(-Vx) = |
|||
|
dx |
7 |
dx |
3 |
£ ( - V I ) | / ( - ^ ) .
Исходная функция у = -х3 монотонно убывает, обратная функция (у = -х1/3) также монотонно убывает, поэтому ее производная меньше нуля.
Итак, в случае монотонно возрастающей функции у - <р(х), когда и обратная функция^ = ц/(х) тоже монотонно возрастает, а производная у'{х)
I юложител ьна^меем |
|
FY (х) = p(Y < х) = р(ф) < х)) = р(Х < И*)) = F( К*)); |
(10-4) |
d_ |
(10.5) |
/У (х) = —Fy (х) = ¥\x)f(¥(x)). |
|
dx |
|
Если же функция^ = ср{х) монотонно убывает, то монотонно убывает и |
|
ее обратная функция^ = у/(х), а производная у/'(х) < 0, поэтому |
|
Fy(x) = p{Y < х) = р(<р(Х) < х)) = р(Х > у/{х)) = 1 - F( у/(х)); |
(10.6) |
/у (*) = ^Fy (х) = \vXx)\f{y,{x)). |
(10.7) |
Формула (10.7) пригодна и для случая монотонно возрастающей функции <р(х\ ведь модуль положительного числа равен самому числу.
95

10.4. Примеры решения задач
10.4.1. Задан график функции плотности вероятности fix) случайной величины X. Построить график функции плотности вероятности fy(x) случайной величины У = X + С, где С - данное число.
Решение. ф(х) = х + С; у/(х) = х - С; у/\х) = 1. Тогда fY (х) = / ( х - С).
График функции /у(х) получается из графика функции fix) сдвигом последнего вправо на величину С (рис. 10.1).
Ах) |
Ш =fix-Q |
|
1 |
|
• |
х |
|
|||
|
Рис. 10.1 |
|
|
10.4.2. Дан график функции распределения F\x) случайной величины X. Описать график функции распределения Fy(x) случайной величины У = -X.
Решение.
FY (х) = p(Y < х) = р{-Х < х) = р(Х > -х) = 1 - F(-x).
График функции FY(x) получается, если график функции F(x) зеркально отразить относительно оси ординат и каждую ординату вычесть из единицы.
10.4.3. Случайная величина Л'задана плотностью вероятностных). Найти плотность вероятности следующих случайных величин:
• а ) У = - 2 |
Л > 3 ; б)У = ех; в ) У = | А ] . |
Решение. |
|
а) Функция У = -2Х+3 монотонно убывает с ростом значений х, значит
= V'(x) = - i , Мх) = ±.дЦ±).
б) Если (р(х) = ех, то ц/(х) = lnx, х > 0 ; у/'(х) = —, поэтому
X
[0, еслих<0,
— • /(In х), если х > 0.
в) Функция У = \Х\ не является монотонной,
flAl<xi = -(0' е с л и * * 0 ;
[Р(~х <Х<х) = F(x)- F(-x), еслих > 0. Следовательно,
Г0, еслих<0,
(Х)= [/(*) + / ( - х ) , если х > 0.
10.4.4.Случайная величина А" задана функцией плотности вероятности
|
|
|
|
— , |
|
х e l — , — ) , |
|
|
|
|
|
|
|
||
|
|
|
|
л- |
|
2 |
1 * |
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
в остальных случаях. |
|
|
|
|
|
|
|||
Описать |
|
функцию плотности вероятности /у(х) случайной |
|||||||||||||
|
|
|
|
||||||||||||
Величины У - s'm(X) и найти вероятность события {0 <у < 1}. |
|
|
|||||||||||||
Гашение. |
На |
интервале |
( - | , |
|| фушсция |
<p{x) = sm{x) |
монотонно |
|||||||||
возрастает; у/(х) = arcsinx; |
у/\х) = |
1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||
Если |
У |
- |
sm(A), то значения |
случайной |
величины |
У |
лежат в |
||||||||
интервале (-1, |
1), следовательно, |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
К |
х<=(-\; |
1), |
|
|
|
|
|
|
|
|
|
|
|
0 |
в противном случае. |
|
|
|
|
|
|||
|
|
р(0 |
< у < 1) |
= |
j-j=L=.—dx = |
iarcsi |
1 |
=1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
arcsinx |
о |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10.4.5. |
Имеется |
|
непрерывная случайная величина |
X с |
плотностью |
||||||||||
-роятности |
fix). |
Найти |
закон |
распределения |
случайной |
величины |
|||||||||
" = тт(Х, |
X2). |
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
min(x,x |
21 \х> если х < 0 ил и х > 1; |
|
|
|
|
|
|
||||||||
) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
х , |
|
е с л и 0 < х < 1 . |
|
|
|
|
|
|
|
|||
Отсюда |
(р(х) = |
\х, |
х*(0; |
1), |
|
х, |
|
х * ( 0 ; |
1), |
||||||
|
х е ( 0 ; |
1). |
К*) = Л , |
|
|
|
|||||||||
|
|
|
|
|
|
\х\ |
* е ( 0 ; |
1). |
|||||||
|
|
1> |
|
|
хе(0; |
1); |
|
л * ) , |
|
* * ( 0 ; |
I); |
|
|||
Ч/\х) |
= |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
ил |
|
|
|
|
|
4=/(Vx"), |
х е ( 0 ; 1). |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
97
10.5. Числовые характеристики
непрерывных |
случайных |
величин |
Математическим ожиданием непрерывной случайной величины X называется число, определяемое по формуле
М(Х) = \xf{x)dx. (Ю.8)
Предполагается, что несобственный интеграл сходится абсолютно; в противном случае говорят, что случайная величина X не имеет математического ожидания. Если случайная величина X принимает значения на конечном интервале (а; Ь), несобственный интервал заменяют
интегралом с конечными пределами: |
|
h |
|
M{X) = \xf{x)dx. |
(Ю.9У |
а |
|
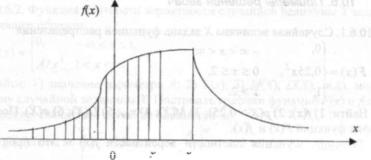
Модой непрерывной случайной величины X называется |
такое значение |
хт0, в котором достигается максимум функции плотности вероятности /(х). '< Медианой хте непрерывной случайной величины X называется такое ее
значение, для которого справедливо равенство |
|
|
||
р(Х<хте) = р(Х>Хте) = 0,5. |
|
(10.10), |
||
Пример моды и медианы показан на рис. 10.2. |
|
|||
Заштрихованная площадь равна 0,5. |
|
|
||
Дисперсия |
Щ.Х) непрерывной случайной |
величины |
X определяется |
|
формулой |
|
|
|
|
ЩХ) |
=](х- |
M(X))2f(x)dx = M[x -М(Х)]2 |
= М{Х2) |
-М2(Х) = |
= |
jx2f(x)dx-M2(X). |
|
( ю . п ; |
|
Предполагается, что несобственный интеграл сходится. По самому
определению дисперсии она не можег быть отрицательной, D(X) > 0. |
|
||
Среднее квадратическое отклонение определяется формулой |
|
||
a{X) = ax=\jD{X). |
|
(10.12); |
|
Если Y •* (р(Х), то математическое ожидание (если оно существует) |
|||
случайной величины К равно |
|
|
|
со |
со |
|
|
M(Y)= [xfY{x)dX= \ |
x\y/\x)\f (у(х))ах, где у/{х) |
- функция, обратная |
к |
- 0 0 |
- о о |
|
|
функции <р(х). Обозначим теперь ^(jc) через и, |
тогда аи = ц/\х)ах; х = |
| |
|
<р(и), а математическое ожидание величины Y выражается интегр&юм
СО |
0 0 |
|
M(Y)= J <p(u)f(u)du = |
j<p(x)f(x)dx. |
(Ю.13) |
- о о |
- О О |
|
(Ведь аргумент подынтегральной функции можно обозначить как угодно).
|
|
|
|
|
"•те Лто |
|
|
|
|
|
|
|
|
Рис. 10.2 |
|
|
|
Точно так же доказывается, что |
|
|
|
|
||||
D{Y)= |
) [x-M(Y)]2fy(x)dx= |
][<p(x)]2f(x)dx-M2(Y). |
(10.14) |
|||||
|
— 0 0 |
|
|
|
- 0 0 |
|
|
|
|
|
|
|
3 0 |
|
|
|
|
Поэтому |
М{аХ |
+ Ь)= |
J(ax + b)f(x)dx = aM(X) + b; |
|||||
|
|
|
|
-со |
|
|
|
|
|
|
ОС |
|
|
|
|
|
|
D(aX |
+b)= |
\{ах |
+ |
b)2f(x)dx |
-M2(aX + |
b) = |
a2D(X), |
|
|
|
-ОО |
|
|
|
|
|
|
i ле a, b - константы. |
|
|
|
|
|
|
||
В частности, |
М(ау а; |
Д а ) - 0; |
М{аХ) - |
аМ(Х); |
D(aX) cfDiX). |
|||
Другие свойства математического ожидания и дисперсии, доказанные для дискретных величин, также остаются справедливыми и в случае
непрерывных случайных величин. |
|
|
|||
Начальный момент |
k-го |
порядка ак |
определяется формулой |
|
|
|
+ 0 0 |
|
|
|
|
<хк =М(Хк)= \xkf(x)dx. |
|
|
(10.15) |
||
Центральный момент к-го порядка |
рк определяется формулой |
|
|||
рк |
=М(Хк) |
= |
М(Х-М(Х))к |
=*j[x-M(X))kf(x)dx. |
(10.16) |
08 |
99 |
Для моментов нечетного порядка предполагается абсолютная сходимость интегралов.
Математическое ожидание - это начальный момент первого порядка, дисперсия - центральный момент второго порядка. Центральный момент первого порядка, очевидно, равен нулю.
10.6. |
Примеры |
решения |
задач |
|
10.6.1. Случайная величина X задана функцией распределения |
||||
|
0, |
- со < х < со, |
||
F(x) = - 0,25х2, |
0 < х < 2 , |
|
||
|
1, |
х > 2. |
|
|
Найти: |
1)Дх); |
2)р(Х> 0,25); 3) М(Х)\ А)хш; 5)ЩХ); 6) о(Х). Построить |
||
график функций F(x) и fix). |
|
|||
Решение. Функция плотности вероятности fix) - это производная |
||||
функции распределения, поэтому |
|
|||
|
ГО, |
- со < X < оо, |
|
|
/(х) = • 0,5х, |
0 < х <. 2, |
|
||
|
0, |
х > 2. |
|
|
Графики функций Fix) и fix) |
приведены на рис. 10.3. |
|||
|
О |
О |
|
|
|
|
|
|
Рис. 10.3 |
|
|
|
|
Определим числовые характеристики. |
|
|
|
|
||
MiX) |
= |
\xfix)dx = \0,5x2dx =3-2 |
|
|
|
|
|
|
|
х 4 2 |
16 |
2 |
|
DiX)= |
Jx2 |
/(x)<fr-(4/3)2 = | 0 , 5 x 3 ^ - 1 6 / 9 |
= - |
- - = |
- ; |
* x |
|
о |
о |
8 о |
y |
y |
3 |
Максимум плотности вероятности достигается при х = 2, хто = 2. По определению медианы, р(Х < хте) = 0,5, тогда
0 , 2 5 x 2 e = 0 , 5 = * x m e = V 2 .
Осталось определить вероятность р(X > 0,25).
piX > 0,25) = /7(0,25 < X < 2) = F(2) - F(0,25) = 1 - 0,253 = 0,984. 10.6.2. Функция плотности вероятности случайной величины X задана
следующим образом:
/(*)« |
(0, |
- о с < * < 1 , |
А/х , |
1 < х < о о . |
Найти: 1) значение параметра А; 2) F(x); 3) MiX), Щ.Х), о\Х), моду и медиану агучайной величи!1ы X. Построить графики функций F(x) wfix).
Решение. Вычислим значение параметра Л.
\ f(x)dx |
= l=> |
JA/x4ax = |
l=>- |
А |
= А/3=>А = 3. |
|
|
|
|
|
Зх: |
|
|
|
|
|
|
|
|
X |
Найдем |
функцию распределения |
F(x)=30jf(t)dt. |
||||
Если х < 1, то Fix) = 0. |
Пусть х > 1, тогда |
|||||
0 |
х |
|
|
х |
|
|
Fix)= J0dt+\3/tAdt = |
-\/P |
= |
1-1/хг- |
|||
-00 |
I |
0. |
|
х < 1 , |
|
|
|
|
|
|
|
||
Окончательно |
F(x) = |
1 - |
|
х > 1 . |
|
|
|
|
|
|
|
||
Графики функций F(x) и fix) показаны на рис. 10.4.
Рис. 10.4
Определим числовые характеристики случайной величины X.
100 |
101 |
|
