
1282
.pdf
M{X) = |
00 |
3 |
= — |
- 3 |
00 |
|
|
|
|
|
|
\x--dx |
|
=1,5. |
|
|
|
|
|||||
|
1 |
X |
|
|
2-Х |
i |
|
|
|
|
|
|
|
|
|
|
|
|
-2,25 = 0,75; |
a(X) = Д 7 5 = 0,867. |
|||
Моды у нашей случайной величины |
нет, так как |
в условии скачано, |
|||||||||
что./(1) - 0. |
Медиану определим, зная, что р(Х < хте) = 0,5. |
|
|||||||||
p(X<xme) = 0,5^F(xme) = |
0,5=>\--{- = |
0j=> х3те = |
2, x w , = l , 2 6 . I |
||||||||
10.6.3. Случайная |
величина X имеет такую плотность вероятности: |
||||||||||
/(х) = Ле'** |
|
при |
х £ 0; |
Дх) = 0, если х < 0. |
При этом /. > 0. |
Найти \ |
|||||
математическое ожидание и дисперсию случайной величины Y «• е |
, |
||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
M(Y)= |
] |
e"f(x)ax |
|
= |
] |
е~хЯе^dx = |
|
|
|
|
|
|
|
|
|
|
|
о |
|
Л + 1 |
|
|
|
i |
|
|
|
U+u |
J |
|
U+i, (Я+2ХД + 1)2 I |
||||
10.6.4. Случайная |
величина X имеет плотность вероятности Дх). П у с т |
||||||||||
y=min(Ar, а), где о - данное число. Найти M(Y) и ДУ). |
|
|
|||||||||
Регпение. |
|
|
|
|
|
|
|
|
|
|
|
ос |
|
|
|
|
|
|
а |
оо |
о |
|
|
А/(К)= J тш (х,я)Дх )Л= Jx/(x)a!x+|a/(x)dx= Jx/Yx)<& + ^(ЛГ > a).
-ОО |
|
-ОС |
fl |
|
—oo |
D(Y)= |
] |
[min(x,a)]2f(x)dx-M2(Y)= |
|
J |
x2f(x)dx + ]a2f(x)dx-M2(Y) |
-ao |
|
|
-ж |
|
a |
—00
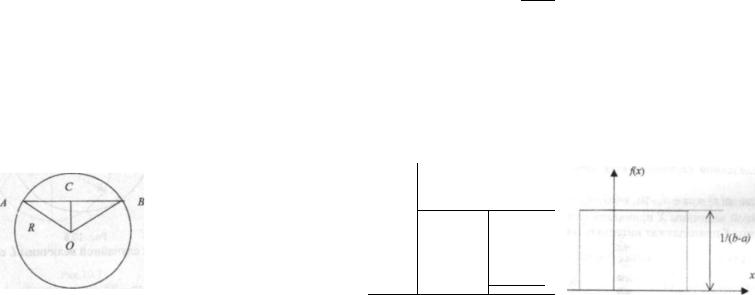
10.6.5. В книге "Воспоминания" генерала А.И. Деникина приводится такой эпизод учитель математики предложил гимназистам найти среднее арифметическое хорд круга (задача из математического журнала за 191(1 год). Юный Деникин представил решение, за которое он получил оценкя "отлично". По всей видимости, оно было таким (рис. 10.5).
Будем проводить хорды параллельно друг другу. Заменим каждун хорду отрезком, длина которого равна искомому среднему арифметическому; обозначим эту длину через х. Получится прямоугольник, высота которого равна 2R, а ширина равна х. Площади этого прямоугольника равна 2Rx - тг/с, откудах = жЯ2.
Предложенное решение трудно назвать строгим. Ведь хорды не обязательно проводить параллельно друг другу. Круг можно заполнить хордами, если проводить их иэ одной точки (рис. 10.6).
Заменяя каждую хорду отрезком длины х, получим полукругплощадью ях'/2 - KR2, откуда х = R^2 .
Это решение ничем не хуже предыдущего. Можно предположить и другие ответы. Какой же из них правильный?
х
Z 5>
Прежде всего, сам вопрос задачи сформулирован некорректно. Что такое "среднее арифметическое" всех хорд? Ведь понятие среднего арифметического определено для конечного множества слагаемых. Множество же хорд круга несчетно. Чему равно "число слагаемых" при вычислении такого "среднего арифметического"?
Подойдем к задаче с вероятностной точки зрения. В круге наудачу выбирается хорда, какова ее средняя длина? Понятие "математического ожидания", вполне строгое, сменит расплывчатое понятие "среднего арифметического" для несчетного множества слагаемых. Но и высказывание "в Kpyi-е наудачу выбирается хорда", как уже было показано, тоже неточное. 11ространство Q можно определить по крайней мере тремя разными способами, которым соответствуют три разных вероятностных пространства и, значит, три разные функции распределения случайной величины L - длины хорды. Разберем эти три случая в том же порядке, что и ранее. В каждом случае мы предполагаем возможным использовать формулу геометрических вероятностей.
1. На окружности зафиксирована точка А и наудачу выбирается точка В, другими словами, наудачу выбирается угол между диаметром АОА\ и хордой АВ (рис. 10.7).
В качестве Q возьмем множество значений угла а: 0 й а < п/2 (ранее мы рассматривали другое множество Q - множество точек окружности).
Вероятность события {а <х} равна
102 |
103 |

|
о . |
х < 0 ; |
F(x) = p(a<x) = |
— , |
0 < х < л 7 2 ; |
|
л/2 |
|
|
1, |
х^л/2. |
|
0, |
x < 0, |
/ ( x ) = - F ( x ) = |
2/л-, |
0<х<л/2, |
dx |
0, |
х>л/2. |
|
AB = 2Rcos(a)
Рис. 10.7
Случайная величина /. - длина хорды АВ - равна произведению
2/?cos(a), значит,
/г/2 |
4 ^ |
*/2 |
4 ^ |
A/(Z,) = f |
(2/^)-2/?cos(a)c/a = — sin(or) |
= —. |
|
о |
* |
о |
* |
2. Случайным образом выбирается середина хорды - одна из точек круга. Пространство элементарных исходов Q - это множество точек круга (рис. 10.8).
Если DE = х, то для того, чтобы длина хорды АВ была меньше х, нужно, чтобы ее центр С лежал вне круга радиуса OF с центром в точке О.
Вероятность этого события равна отношению площадей кольца и круга.
р(АВ < х) = |
^ |
— = — j" 0<x<2R. |
|
пЯ7 |
4R2 |
Функция распределения случайной величины L - длины хорды АВ -
такова:
0. |
х < 0 ; |
|
|
|
|
|
||
F(x) = |
0 <, х < 2R; |
|
|
|
|
|
||
4R |
|
|
|
|
|
|
|
|
|
x>2R. |
|
|
|
|
|
||
|
|
DE=x; |
|
DF2 |
= R2 - — |
|||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
F |
\ |
|
|
|
|
D / |
|
|
||||
|
|
|
|
|
|
|
||
|
|
R |
|
|
|
|
|
|
|
|
|
|
V о J |
|
|
|
|
Рис. 10.8
Плотность вероятности случайной величины L следующая:
f0, |
х < 0 ; |
FIX)' |
0<x<2R, |
2R',2 ' |
|
[0, |
х > 2R. |
Средняя длина хорды равна |
|
2R х2 |
|
|
2 R - U . |
о 2R2 |
6R' о 3 |
Число Rл/2 - медиана случайной величины L .
3. Случайно выбирается расстояние г от хорды до центра круга. Пространство элементарных исходов П - отрезок [0, R); функция распределения случайной величины X - расстояния от хорды до центра
круга - такова:
Кг<0 ;
F(r) = p(X<r) = - , |
0<_r,R; |
1, г > R.
104 |
,05 |
Соответственно функция |
плотности вероятности случайной величины X |
такова: |
|
ГО, |
г < 0 ; |
/(/•) = • 1/Л, |
0<r<R; |
1, |
r>R. |
Длина хорды АВ равна величине 2\IR2 -Г2 (рис. 10.9).
Тогда математическое ожидание случайной величины L - длины хорды А В - равно
M(L) = f2VR2 - г2 —dr. Произведем замену переменной,
оR
г т R • sin(r), |
*'} |
J |
•> |
|
лЛ |
dr = R cos(0 dt, M(L) = 2R |
cos |
2 |
{t)dt = —. |
ОС = r
|
|
|
|
|
Рис. 10.9 |
|
Все три |
полученных ответа правильны. |
|||||
10.7. |
|
|
Равномерный, |
показательный |
||
и |
|
нормальный |
законы |
распределения |
||
|
|
|
10.7.1. Равномерное распределение |
|||
Функция |
плотности |
вероятности равномерного закона такова: |
||||
|
[0, |
|
х<а; |
|
|
|
/ ( * ) = |
|
1 |
а < х < Ь; |
(10.17) |
||
Ъ-а |
||||||
|
|
|
||||
|
[0, |
|
х>Ь, |
|
||
где а и b - данные числа, a<b;avib- это параметры равномерного закона. Найдем функцию распределения F(x) равномерного закона. Если х < а, то
106
* |
|
|
|
|
|
|
|
а |
х |
« |
F ( x ) = |
/0-<# = 0 . Е с л и а < х < |
А, то F(x)= |
[0-dt+ |
\——dt = ^—^, |
||||||
|
|
|
|
а |
ft |
|
j |
х |
|
|
Когдах>6, |
F ( x ) = |
f 0 - A + f |
|
А + | Ь - а 7 = |
1.Итак, |
|
||||
|
|
|
|
|
|
аЪ~а |
Ь |
|
|
|
|
|
|
0, |
|
еслих<а; |
|
|
|
||
F(x) |
= |
\ |
х - а |
|
если а < х < Ь; |
|
(10.18) |
|||
|
|
|
Ъ-а' |
|
|
|
|
|
|
|
|
|
|
1, |
|
если х > Ь. |
|
|
|
||
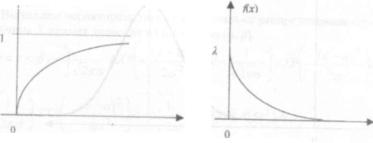
Графики функций F(x) иДх) показаны на рис. 10.10.
iI F(x)
1
•
а |
0 |
а |
О |
Рис. 10.10
Определим числовые характеристики равномерного распределения.
M{X)=\xf{x)dx=\-±-dx |
= |
|
|
а + Ь |
|
(10.19) |
||
|
|
2 |
|
|
||||
|
>аЪ-а |
|
Tib-а) |
|
|
|
||
D(X)= |
jx2 f(x)dx - |
ь |
= |
х2 |
'a + |
b}2 |
|
(10.20) |
М2(X) |
j~—dx- |
|
|
|
||||
|
|
„о — a |
2 |
, |
12 |
' |
||
b-a |
|
|
|
|
|
|
|
(10.21) |
o-r ~ 2V3 |
|
|
|
|
|
|
|
|
Очевидно, что моды нет, а медиана равна математическому ожиданию. Вероятность попадания в интервал (a, /?) равномерно распределенной
случайной величины задается следующей, легко выводимой формулой:
107
|
О, |
|
|
если Р < а или b <, а; |
|
Р-а |
|
' 1 |
|
|
Ъ- |
а |
|
|
|
|
|
||
р(а < х < ру |
fi- а |
» |
(10.22) |
|
|
|
|||
|
Ъ- |
|
|
|
|
а |
|
|
|
|
Ь- |
а |
|
|
|
|
|
|
|
|
Ъ- |
а |
|
|
|
1, |
|
|
если а<а<Ь< р. |
Равномерным распределением можно аппроксимировать ошибки измерений, когда измеренное значение округляют до ближайшего целого на шкале измерительного прибора.
Найдем закон распределения линейной функции Y равномерно
распределенной случайной величины X, Y = (сХ + d), |
|
где с, d - |
данные |
||||||
числа. |
|
|
|
|
|
|
|
|
|
Если |
<р(х) = cx+d, |
то у/(х) = (х- d)/c, |
у/(х) = \1с. |
Когда значения |
|||||
случайной |
величины X принадлежат интервалу (а, Ь), значения случайной |
||||||||
величины К принадлежат интервалу {са |
+ d; cb |
+d); следовательно, |
|
||||||
/00 = |
|
^ |
если xe(ca + d, cb + d); в |
противном |
случае |
||||
|
|
Ь-а |
|
|
|
|
|
|
|
Д х ) = 0. |
|
|
|
|
|
|
|
|
|
Вновь |
|
получено |
равномерное |
распределение |
- |
на этот |
раз н |
||
интервале (са + d, |
cb + d). (Если с < 0, то левая граница интервала - числ |
||||||||
cb +d, правая - число са + d).] |
|
|
|
|
|
||||
10.7.2. Показательное распределение
Случайная величина X имеет показательное распределение, если плотность вероятности задается формулой
\Л-е~х, если х £ 0 ;
(10.23)
[о, если х < 0.
Параметр закона Я должен быть больше нуля.
Опишем функцию распределения F(x) показательного закона. Если х < 0,
то, очевидно, |
F(x) = 0. Пусть х > 0. Тогда |
|
F(x) = |
J f(t) |
dt=\X- e~hdt = -e -At -1 - е_Ях, таким образом |
-co |
0 |
|
|
|
108 |
fo, |
если x < 0; |
|
|
F(x) = |
(10.24) |
||
|
|||
[1-е |
м, еслих> 0. |
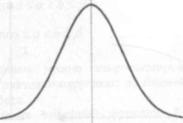
Графики функций F(x) и / t » показаны на рис. 10.11.
Рис. 10.11
Найдем числовые характеристики показательного распределения.
М(Х) = |
jxAe^dx =(-хе-* |
- - |
) |
|
(10.25) |
|
|
о |
|
Я |
|
|
|
|
|
|
|
|
||
М(Х2) |
= )х2ЯеАхах |
=(-xV" |
- ^хе'* |
~ e ~ * " T = -|- |
|
|
D{X)=M(X2)-M2(X) = |
-^; |
1 |
сг(х) = |
-. |
|
|
|
(10.26) |
|||||
|
|
|
Я |
я |
|
|
|
|
|
|
|
||
Ясно, что мода равна нулю. Найдем медиану. Из условия |
|
|||||
F(xme) = |
0,5 = 1 - е |
**~ |
следует, что |
хте = ^. |
|
|
|
|
|
|
|
(-Я) |
|
Вероятность попадания в интервал (а, /?), /? > а £ 0, равна |
|
|||||
р(а<х<Р) = F(P)-F(a) = е~Аа |
-е**. |
|
(\0.27) |
|||
Показательное распределение используется, например, в теории массового обслуживания.
10.7.3. Нормальное распределение
Случайная величина X распределена по нормальному закону (закону I аусса), если ее плотность вероятности задается формулой
1 |
(х-а)2 |
2а2 |
|
у[2лсг |
, - с о < х < оо, |
|
109
где - ос < а < ос иа> 0 - параметры закона.
График функции плотности вероятности нормального закона показан на рис. 10.12.
ЯХ)
а
Рис. 10.12
График симметричен относительно прямой х - а.
Ниже показательная функция е* будет иногда обозначаться ЕХР{х) для удобства чтения текста.
Найдем числовые характеристики нормального закона. Ясно, что моде и медиана вследствие наличия оси симметрии равны а.
Положим |
|
= |
t, тогда dx-odt, откуда |
|
|
|
|
|
|
||||
(7 |
|
|
|
|
|
|
ЩХ) = - т = = |
](оТ |
+ a)EXP(-0,5t2 |
)dt = -^= JEXP(-0,5t2 |
)dt |
- |
|
£A7>(-0,5/2 ) |
|
= a, так как |
\EXP(-Q,5t2 )dt = -Jbr - |
это |
известный^ |
|
из курса анализа интеграл Пуассона.
Математическое ожидание нормального закона равно значении^ параметра а.
ЩХ2)= ) ^ I ^ J J L Z L F \ I X = ] Ц ^ £ * Р ( - 0 , 5 , 2 > Л =
(-tEXP(-Q,5t2) |
42к 2ao EXP(-0,5t2) |
+ -£=V27 = |
4ъг |
|
<2n |
=аг+а\
Итак, ЩХ) - о2, а(Х) = а. Среднее квадратическое отклонение нормально распределенной случайной величины равно значению параметрам.
Вычислим вероятность того, что нормально распределенная случайная величина А" примет значение из интервала (а, В).
* а < х < Л - ] |
• |
S |
H |
f - ^ b - - |
I |
*<RJ |
• |
||
|
|
аы2ло |
|
. |
2а |
|
|
|
|
|
|
|
|
|
|
Р-а |
|
|
|
^ Ш ^ к ф |
|
|
j |
£ Щ - 0 , 5 г 2 ) * 7 - |
|||||
1 |
| £ |
Л7>(-0,5г)*7. |
|
|
|
|
|
||
|
|
|
|
|
|
||||
2л- о |
|
|
|
|
|
|
|
|
|
Функция |
|
|
|
|
|
|
|
|
|
|
Ф(.х) = - |
= |
|
|
|
|
|
(10.28) |
|
|
|
л/2ж о |
|
|
|
|
|
|
|
называется функцией Лапласа. Для нее составлены таблицы, по которым, зная аргумент х, можно найти величину Ф(х). Можно, конечно, решить обратную задачу: по значению функции Лапласа найти значение аргумента.
Укажем три простых свойства функции Лапласа:
|
1 |
о |
-г |
1. |
ф(0) = -±=\е |
2rfr = 0. |
|
V 2 > 4
1^4
2.Ф(оо) = -=\е 2dV = 0,5. v2x 0
На самом деле уже для значений аргумента х > 5 можно считать, что </>(*) = 0,5.
Ji
3. <P(-x) = -1= f e 2dt = -0{x). V2/r о
Таким образом, функция Лапласа нечетна.
110 |
111 |
|
Мы показали, что |
|
|
р(а<х<в) = фф^-) - |
Ф ( — ) • |
(10.29] |
о |
а |
|
Теперь легко описать функцию распределения F(x) нормального
закона с параметрами |
а и ст. В самом деле |
|
F(x) = р( X < х) = р(-оо < X < х) = Ф ( — ) - Ф(-оо) |
= Ф(—) + 0,5. |
|
|
о |
о |
F(x) = <Z>(^-^) + 0,5 |
(10.30] |
|
о |
|
|
В некоторых пособиях по теории вероятностей приводятся таблицы
функции |
|
1 |
|
Фх (х) = —Р=Г= \е |
2 dt. Нетрудно видеть, что Ф, (х) = 0,5 + Ф(х), |
так что р(а < х < /?) = ФЛ^—^) -Ф,(—-).
аа
Иногда приводится таблица значений функции
2 * -'- |
|
|
|
|
|
ф 2 (*) = -= \е |
2dt, |
Ф2(х) = 2Ф,(х), поэтому |
|
||
л/2/r о |
|
|
|
|
|
р(а<х <fi)-U |
Ф 2 ( ^ - - а ) - Ф 2 ( — ) ]. |
|
|||
|
2 |
а |
о~ |
|
|
Для интервала |ЛГ - |
а\ < д имеем |
a = a-S, p = a + S, поэтому |
|
||
р{\ X - а | < 8) = Ф{-) |
- Ф(- -) = |
2Ф(-). |
(10.31) |
||
|
о~ |
о~ |
о~ |
сХ + Щ |
|
Опишем еще закон |
распределения линейной функции У = |
||||
нормально распределенной случайной величины X, где с и d - заданные числа. Случайная величина У принимает значения на всей числовой оси.
|
1 |
|
(x-d- ас)' |
||
|
|
|
|
ЕХР |
|
|
42лсг |
|
2(с*У |
||
Получена |
функция плотности |
нормального закона с параметрам' |
|||
а] = са + d, (7| |
= |с|<7. |
|
|
||
Линейная функция нормально распределенного аргумента также нормально распределена.
Нормальное распределение довольно часто встречается при решения практических задач. В приложении приведена таблица нормального распределения (таблица функции Лапласа).
10.8. Примеры решения задач
10.8.1.Минутная стрелка электрических часов перемещается скачком
вконце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на двадцать секунд.
Решение. Случайная величина X, о которой идет речь в задаче, - это разность в секундах между истинным временем и временем, которое показывают часы. Из условия задачи можно заключить, что часы только опаздывают, а сама разность - это равномерно распределенная на отрезке 10, 60J случайная величина (ее значения образуют пространство
элементарных исходов). Требуется найти |
вероятность р(Х < 20). Таким |
образом, о=0, Ь~ 60, ЫХ<20)=р(0<Х <20) - (2°"°^ = I. |
|
|
( 6 0 - 0) 3 |
10.8.2. На отрезке длины 1 случайным |
образом выбирается точка. Ею |
отрезок делится на два «куска», вообще говоря, разной длины. Какова средняя длина меньшего куска? Чему равно среднее отношение длин кусков отрезка?
Решение. Случайная величина А' - координата точки на отрезке - имеет равномерное распределение с параметрами a = 0, b = 1. Но тогда случайная величина К-длина меньшего куска - равномерно распределена на отрезке (0; 0,5), поэтому М(У) = 0,25.
Отношение длин короткого и длинного кусков - это случайная
величина Z, равная |
|
|
|||
z= т\п(Х, |
1-Х) |
1-Х |
X < 0,5; |
||
тах(Х, |
1 - X) |
1-Х |
|
||
|
|
|
|
X |
1 > X > 0,5. |
|
|
|
|
|
|
Отсюда |
|
|
|
|
|
0,5 |
|
|
1 1 - г |
|
|
M(Z)= J |
|
|
dx+ |
J — - d t c = -21n(0,5)- 1 = 0,386. |
|
|
|
||||
0 1 ~ X |
0.5 X |
|
|||
10.8.3. Непрерывная случайная величина X распределена по показательному закону с параметром Я=3. Найти вероятность того, что в результате испытания Л'попадет в интервал (0,13; 0,7).
Решение. р(0,\3 <х< 0,7) = е~л°'13 -е~л°'7 = 0,555.
10.8.4. Вывести правило "трех сигм": вероятность того, что модуль отклонения нормально распределенной случайной величины от ее
112 |
113 |
Мы показали, что |
|
|
|
||
р{а<х<Р) = Ф{^-) - Ф{^-^). |
|
(10.29 |
|||
Теперь легко |
описать функцию |
распределения F{x) |
нормального |
||
закона с параметрами а и а. В самом деле |
|
||||
F(x) = р(Х |
< х) = /К-оо < X < х) = Ф(^-) - Ф(-ос) = |
Ф(^-) + 0,5. |
|||
/г(х) = ф ( ^ _ ^ ) + 0,5 |
|
(10.30) |
|||
|
|
||||
В некоторых пособиях по теории вероятностей приводятся таблицы |
|||||
функции |
|
|
|
|
|
Фх(х) = ~j== |
je |
2 dt. Нетрудно видеть, что Ф,(х) = 0,5 + Ф(х), |
|||
так что р(а < х |
< |
0) = |
ФА& °)-Фх(——-). |
|
|
Иногда приводится таблица значений функции |
|
||||
2 |
' |
^ |
|
|
|
Ф2 (х) = -j== je |
2dt, |
Ф2(х) = 2Фх(х), поэтому |
|
||
р(а <,</*) Л [ Ф 2 |
( ^ а ) - Ф 2 |
( ^ ) ] . |
| |
||
|
2 |
о |
а |
|
|
Для интервала \Х - а\ < д имеем |
a = a-S, ft = a + S, поэтому |
||||
/<! X - а I < S) = Ф ( - ) - Ф(--) = 2Ф{-). |
(10.31), |
||||
|
|
а |
о |
а |
|
Опишем еще закон распределения линейной функции У = сХ + л нормально распределенной случайной величины X, где с и d - заданные] числа. Случайная величина К принимает значения на всей числовой оси.
|
1 |
|
(x-d- |
ас)' |
||
|
\2па |
ЕХР |
2(са): |
|
|
|
|
|
|
|
|
||
Получена |
функция плотности |
нормального закона с параметрам*! |
||||
в) = ca + d, СТ| |
- \с\а. |
|
|
|
|
|
Линейная функция нормально распределенного аргумента так"
нормально распределена.
Нормальное распределение довольно часто встречается при решении] практических задач. В приложении приведена таблица нормального распределения (таблица функции Лапласа).
10.8. Примеры решения задач
10.8.1.Минутная стрелка электрических часов перемещается скачком
вконце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на двадцать секунд.
Решение. Случайная величина X, о которой идет речь в задаче, - это разность в секундах между истинным временем и временем, которое показывают часы. Из условия чадачи можно заключить, что часы только опаздывают, а сама разность - это равномерно распределенная на отрезке [0, 60J случайная величина (ее значения образуют пространство элементарных исходов). Требуется найти вероятность р(Х < 20). Таким
образом, о=0, Z>-60, ЫХ<20)=Ы0<Х<20)~ (20~°) = 1
^(60 - 0) 3
10.8.2.На отрезке длины 1 случайным образом выбирается точка. Ею отрезок делится на два «куска», вообще говоря, разной длины. Какова средняя длина меньшего куска? Чему равно среднее отношение длин кусков отрезка?
Решение. Случайная величина А' - координата точки на отрезке - имеет
равномерное распределение с параметрами a = 0, Ь " 1. Но тогда случайная величина У - длина меньшего куска - равномерно распределена на отрезке (0; 0,5), поэтому М(У) = 0,25.
Отношение длин короткого и длинного кусков - это случайная величина Z, равная
ГY
:,= тт(Х, |
1-Х) |
|
1-Х |
Х<0,5; |
|
|
тах(Х, |
1-Х) |
|
1-Х |
|
||
|
|
|
||||
Отсюда |
|
|
|
|
\>Х> |
0,5. |
|
|
|
|
|
|
|
|
0.5 |
|
I |
, _ |
|
|
M(Z)= |
\ |
dx+ |
J—-dx = -2 ln(0,5) -1 = 0,386. |
|||
|
0 |
1 - X |
0 5 |
X |
|
|
10.8.3. |
Непрерывная |
случайная |
величина X распределена по |
|||
показательному закону с параметром Я=3. Найти вероятность того, что в
результате испытания А'попадет в интервал (0,13; 0,7). Решение. р(0,13 < х < 0,7) = е~Л °'13 -е'я 0,7 = 0,555.
10.8.4. Вывести правило "трех сигм": вероятность того, что модуль отклонения нормально распределенной случайной величины от ее
112 |
113 |
|

Значения системы {X, У) - это упорядоченные пары чисел (х,у).
11.1. |
Функция |
плотности |
вероятности |
системы |
двух |
случайных |
величин |
|
|
Систему (X, У) назовем системой непрерывного типа, если функция распределения F(x, у) непрерывна на всей плоскости и существует такая неотрицательная интегрируемая в бесконечных пределах по каждой из координат кусочно-непрерывная функция fix, у), называемая плотностью вероятности системы {X, У), что
F(x, у)= ) )F(s, t)dsdt. |
(П-2) |
-00 -00
Непосредственно из определения следуют такие свойства функции Дх,
У)'-
1. |
fix,y)>0, -<о<х,у< + <х>. |
|
||||
|
|
д2 |
|
|
|
|
2. |
Д х , у) = |
|
Fix, у)в |
каждой |
точке непрерывности функции |
|
дхду |
||||||
|
|
|
|
|
||
|
fix, у). |
|
|
|
||
3. |
fxix) = ^F{x, |
со)= |
J/(x, |
y)dy; |
||
|
|
ах |
_х |
|
|
|
<fy
СО 0 0
4. F(oo, со)= j If(x, y)dxdy = \.
-0 0 -00
5.Вероятность того, что система {X, Y) примет значение (х, у) из|
некоторой области D, равна значению интеграла Jj/(x, y)dxdy.
(D)
Случайные величины X к У называются независимыми тогда и только! тогда, когда функция плотности вероятности системы представляется в,
виде произведения |
|
J |
|
fix, у) = /хШу(У)- |
<1L3> |
||
Эквивалентное определение независимости: случайные величины Л1 и Y |
|||
независимы тогда и только тогда, когда |
|||
Fix, |
y) = Fxix)FYiy). |
(П.4) |
|
Действительно, |
если |
/(х, у) = fx ix)fy iy), то |
|
Fix, |
у)= |
J |
)fxis)fyit)dtds=Fx{x)FYiy). |
|
-00 -00 |
|
|
Наоборот, если |
F(x, |
у) = Fx (x)FK iy), то |
|
Л * &*%дв*Ъь y)=fxi*)fyiy)-
11.2. Примеры решения задач
11.2.1. Функция распределения системы {X, У) равна F(x, у). Найти вероятность события А = {- со < X < х,, у{ < У < у2 }.
Решение.
р(А) = F(-oo, ух) + F(x,, у2) - F( - cc, у 2 ) - Fix, ,ух) = F(x,, у2) - Fix, ,У]).
11.2.2. Имеются две независимые случайные величины Хм У, каждая из которых равномерно распределена на отрезке (0; а). Написать выражения для функции плотности fix, у) и функции распределения Fix, у).
Решение. Оно не нуждается в дополнительных комментариях.
* |
|
ДО, |
х « ( 0 ; |
а). |
ГГт |
J0, |
у£(0; а). |
|
|
|
|
|
1/а2, О < х , |
у<а; |
|
||
fix, |
У) |
= /х{х)/у{у) |
|
|
|
|
|
|
|
|
|
|
|
в противном случае. |
|||
|
|
0, |
х < а ; |
|
|
|
|
|
Fx{x) |
= х/а, |
х е ( 0 , |
а); |
FK (у) = |
у la, у |
е (О, а); |
||
|
|
1, |
х > а. |
|
|
|
1, |
У>а. |
|
|
|
[0, |
|
х < 0 |
или у<0; |
|
|
|
|
|
ху/а2, |
0<х,у<а; |
|
|||
F{x,y) |
= |
Fxix)FY{y) = х/а, |
0 < х < а, |
у > а; |
|
|||
|
|
|
у la, |
0<у<а, |
xZa; |
|
||
|
|
|
1> |
|
х > а, |
у > а. |
|
|
11.2.3.Пара случайных величин X и У имеет совместную плотность
вероятности |
/ ( х , у ) = а/{\ + х2 |
+х2у2 |
+у2), |
-<я<х,у<ю. |
|
|
|||
1. Найти коэффициент а. |
|
|
|
|
|
|
|||
2. |
Установить, зависимы или нет величины А'и У. Найти fxix) |
и fyiy). |
|||||||
3. |
Найти вероятность события |
А = {-\<Х <\, |
- 1 < У < l}. |
|
|||||
Решение. Так как (1 + х2 |
+х2у2 + у2) = (1 + х2)(1 + у2), |
то случайные |
|||||||
величины X и У независимы, |
fx ( х ) |
= |
, |
fY (у) |
= |
л/^~ . |
|||
|
|
|
|
1 + х 2 |
|
1 |
+ |
у2 |
|
116
Значения системы (A", Y) - это упорядоченные пары чисел (х,д>).
11.1. |
Функция |
плотности |
вероятности |
системы |
двух |
случайных |
величин |
|
|
Систему (A, Y) назовем системой непрерывного типа, если функция распределения F(x, у) непрерывна на всей плоскости и существует такая неотрицательная интегрируемая в бесконечных пределах по каждой из координат кусочно-непрерывная функция Дх, у), называемая плотностью вероятности системы (X, Y), что
F{x, у) = ) )f(s, t)dsdt. |
(11.2)] |
—00 —00
Непосредственно из определения следуют такие свойства функции Дх,
У)-
1. / х , ^ ) > 0 , -<с<х,у< |
+ |
со. |
|
|
|
|
||||||
|
|
|
|
Q2 |
|
|
|
|
|
|
|
Щ |
2. |
Дх, |
у) = |
|
|
F(x, у) в каждой точке непрерывности |
функции , |
||||||
|
|
|||||||||||
|
|
|
|
дхду |
|
|
|
|
|
|
||
|
Ах, У). |
|
|
|
|
|
|
|
|
|
|
|
3. |
fx(x) |
= |
^-F(x, |
|
со)= |
|
] / ( х , |
y)dy\ |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
fy(y) |
= |
|
~F(*, |
|
у)= |
|
\f{x, |
y)dx. |
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
со |
ОС |
|
|
|
|
|
|
|
4. |
F(co, |
оо)= |
J If{x, |
y)dxdy = \. |
|
|
|
|||||
|
|
|
|
—00 |
—00 |
|
|
|
|
|
|
|
5. Вероятность того, что система Щ Y) примет значение |
(х, у) |
и з ] |
||||||||||
|
некоторой области D, |
равна значению интеграла |
\\fix, |
y)dxdy. |
j |
|||||||
|
|
|
|
|
|
|
|
|
(О) |
|
|
|
Случайные |
величины X w |
Y называются независимыми |
тогда |
и только |
||||||||
тогда, когда функция плотности вероятности системы представляется в
виде произведения |
j |
fix, y) = fxix)fyiy). |
(U3H |
Эквивалентное определение независимости: случайные величины А'и Т\ независимы тогда и только тогда, когда
Fix, |
y) = Fxix)Friy). |
|
( П * |
|
Действительно, |
если |
/(х, |
у) = fx ix)fy iy), то |
|
Fix, |
у)= |
J |
)fxis)fyit)dtds=Fxix)FY{y). |
|
|
—00 —00 |
|
|
|
Наоборот, если |
F(x, |
у) = |
Fx ix)FY iy), то |
|
|
|
|
|
116 |
/<*> |
|
|
y) = fxi*)fyiy)- |
|
11.2. |
Примеры |
решения |
задач |
|
11.2.1. Функция |
распределения |
системы (X, Y) равна F(x, у). Найти |
||
вероятность события |
А = {- со < X < х,, у, < Y < у2 }. |
|||
Решение.
р{А) = F(-oo,у х ) + F(x,, у2) - F(-cc,у 2 ) - F(x, , У ] ) = F(x,, у2) - Fix, ,>>,)• 11.2.2. Имеются две независимые случайные величины Хи Y, каждая из которых равномерно распределена на отрезке (0; а). Написать выражения
для функции плотностиДх,^) и функции распределения F(x,^). Решение. Оно не нуждается в дополнительных комментариях.
|
|
Ma, |
у&{0; |
a); |
[О, |
х«(0; а). |
О, |
уг{0; |
a). |
|
Г |
1/а2, 0<х, у<а; |
|
|
f(x, |
y) |
= fxi*)fyiy)A |
|
|
|
|
L 0 |
|
|
0, |
х<а; |
F*ix) |
= |
xla, |
x e ( 0 , a); |
|
|
1, |
х > а. |
впротивном случае.
Оу<а;,
FY{y) = |
у la, |
у е (О, а); |
|
||
|
1, |
У>а. |
О, |
х < 0 |
или у^О; |
xyla2, |
0<х,у<а; |
|
Fix,y) = Fxix)FY{y) = . xla, |
О < х < а, у > а; |
|
yla, |
0<у<а, |
х*а; |
1> |
х>а, |
у>а. |
11.2.3.Пара случайных величин X и Y имеет совместную плотность
вероятности /(х, у) = а /(1 + х2 + х2у 2 +у2), - со < х, у < со.
1.Найти коэффициент а.
2.Установить, зависимы или нет величины А" и Y. Найти/*{х) и fyiy).
3. Найти вероятность события А = {-\<Х <\, -г ШТйЦ.
Решение. Так как (1 + х2 + х2 >>2 + у2) = (1 + х2)(1 + у2), то случайные
величиныXи Yнезависимы, f x ( х ) = |
— |
— , |
fyiy) = |
|
1 + |
х |
1 + у |
117 |
|
|
|

|
00 |
п. |
|
|
Так как |
|
|
|
zrdx = Va • arctg(x) |
_ i l + x |
|
|||
|
2 |
|||
Далее в силу независимости величин А" и У |
||||
р(-\<Х<\, |
-\<Y<\) |
= |
|
р(-\ <Х<, 1)р(-1 < Y < 1) = |
п2
1
/—Ш—ГЛ
11.2.4. Пространство элементарных исходов Q - множество точек квадрата, заштрихованного на рис. 11.1, а. Случайные величины X к Y-4 соответственно абсцисса и ордината случайно выбранной точки. Написать
выражение совместной |
плотности |
вероятности |
fix, у) и плотностей f\(x\ |
f)iy). Зависимы или нет случайные величины X и |
У? |
||
Решение. Условие |
задачи |
предполагает |
постоянство плотности |
вероятности fix, у) всюду в квадрате ABCD (fix, у) = а,(х,у)е ABCD) и
равенство плотности вероятности нулю вне квадрата. Таким образом,
|
|
|
|
|
|
О |
х+1 |
1 |
-х+1 |
/= |
JJ |
f(x,y)dxdy= |
|
JJ |
adxdy = |
jdx J |
ady+jdx \ady - |
||
|
(ABCD) |
|
|
|
(ABCD) |
-I |
-x-1 |
0 |
x-1 |
= |
2 a ( — + |
x) |
+2a( |
|
+ x) = 2a = 1 => a = 0,5. |
|
|||
|
|
|
|
2 |
о |
|
|
|
|
|
Совместная функция плотности вероятности такова: |
||||||||
|
|
|
0,5, если Ы +1 v| < 1; |
|
|
|
|||
|
|
{0, если |
|jc| -н |у| > 1. |
|
|
|
|||
|
|
|
а) |
|
|
|
|
б) |
|
Рис.11.1
Далее (рис.11.1, б)
|
w |
_('-N)2 |
-1<хй0; |
|||
Fx(x) = p(X<x) = |
>ABCD |
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
- JacgfL _ j |
(1 - X)' |
0<x<:\; |
|||
|
'ABCD |
|
|
|||
|
|
|
|
|||
|
1, |
|
|
|
|
x>\. |
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
fo, |
|
|
|
|
|
|
144 |
|
H<i. |
|
||
Аналогично |
|
|
|
|
|
|
fr(y) = |
|
|
Щ |
|
||
|
|
W<i. |
|
|||
|
|
|
|
|
||
|
fo, |
|
|
|
ЩЫ ИЛИ \y\ > 1; |
|
lo-Hxi-W), и , \y\<\.
Так как f(x,у) * fx (x)fY(у), то случайные величины X, Yзависимы. 11.2.5. Система (X, Y) имеет плотность вероятности
U (х2+у2)2'
Требуется определить коэффициент а и найти радиус R круга с центром в начале координат, вероятность попадания в который системы (л, Y) равна 0,5.
Решение.
1 }/<*,y)dxay = l=>) |
J |
jSL^fc^'.V. |
|
|
Перейдем к полярным |
координатам: x = pcos<p, y = psinip, |
|||
х2+у2=р2; |
|
|
|
|
-oo-col + ^+y2)2 |
0 0 1 + /> |
Ol + P4 |
2 |
|
Вероятность попадания системы (ЛГ, У) в круг радиуса Л с центром в начале координат равна
о оя'(1 + р4)
118
119
