1282

событие А, но не входят в событие В. Разность событий - это разност множеств. Событие А\В происходит тогда и только тогда, ког происходит событие А, но не происходит событие В. Легко видеть, чт А = Q \ А. Сами элементарные исходы будем обозначать со.

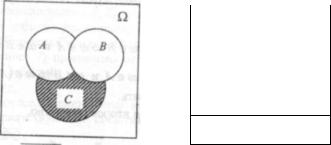
Все данные определения иллюстрируются следующим образом: множество Q изображается прямоугольником, а событие - частями этого прямоугольника (рис. 2.1); это так называемая диаграмма Венна.

Рис. 2.1

Нетрудно убедиться (например, глядя на диаграмму Венна) в

Решение.

а) Будем понимать под элементарным исходом список людей, которые шли в комиссию. Тогда число элементарных исходов равно числу

пособов выбрать двух человек из пяти данных: т.е. с\ =10Выпишем •но множество Q.

р - [(А, В), (А, Б), {А, Г), (А,Д), (Б, В), (Б, Г), (Б,Д), (В, Г), (В,Д), (Г, Д)}

Здесь записи (А, Б) или (Б, А) означают одно и то же.

б) Будем понимать под элементарным исходом число мужчин и число «и шин, вошедших в комиссию. Тогда возможны всего три случая: Q = {(2М), (2Ж), (1М, 1Ж)}, где запись (1М, 1Ж), например, означает, что в

Комиссию вошли один мужчина и одна женщина.

2.4.2. Наугад выбирается одна буква из числа образующих слово «формула». Какие из следующих множеств являются пространством Мементарных исходов для рассматриваемого эксперимента:

1){ф, о, р, м, у, л, а}; 2) {р, м, у, л, а}; 3) (гласная, ф, р, м, л);

4){согласная, у, е}; 5) (гласная, согласная)?

Решение. Если понимать под элементарным исходом выбранную букву, то первое множество можно считать пространством элементарных •сходов, а второе нельзя, так как буквы «ф» и «о», которые могут быть Выбраны, в данное множество не входят.

Пятое множество также можно считать пространством элементарных Исходов, если понимать под элементарным исходом информацию о том, •ыбрана гласная или согласная буква.

Третье множество занимает промежуточное положение между первым И пятым. Под исходом эксперимента понимается информация о том, Гласная или согласная буква выбрана, причем, если выбрана согласная буква, указывается, какая именно.

Четвертое множество не является пространством элементарных Исходов для данного эксперимента. В нем не описаны возможности выбора букв «о» и «а», зато указана букса «е», которой нет в слове формула.

2.4.3. Поезда метро следуют с интервалом в две минуты. Пассажир приходит на станцию в случайный момент времени.

Элементарный исход - время ожидания пассажиром поезда. Описать пространство элементарных исходов.

Решение. Элементарный исход - число из отрезка [О, 2J, пространство > к-ментарных исходов - множество точек отрезка [0, 2], Q = {со | 0 < со <

2.4.4. В данном круге наудачу выбирается хорда. Описать три различных пространства элементарных исходов этого эксперимента.

Решение.

а) Зададим хорду положением ее концов на окружности. Закрепи один из концов в точке А. Тогда выражение «выбрать наудачу хорд:' означает, что на окружности наудачу выбирается точка В (рис. 2.2,а

Пространство элементарных исходов Q - это множество точе^ окружности.

б) Зададим хорду положением ее середины 0\ (рис. 2.2,6). Тогда Q

это множество внутренних точек данного круга.

в) Хорду можно задать расстоянием d от нее до центра круга (0 <d<r .

где г - радиус круга. Тогда Q - множество точек отрезка fO, г], Q = {d \ О ±d<r).

a) Q = {(•) В | ()В е окружности} б) Q = {(•) О, | (•) О, € кругу} Рис. 2.2

2.4.5. А, В, С - три произвольных события. Найти выражения событий, состоящих в том, что из А, В, С:

1)произошло только А; 2) произошли А и В, событие С не произошл

3)все три события произошли; 4) произошло по крайней мере одно ~ событий; 5) произошло одно и только одно событие; 6) ни одно из событ не произошло; 7) произошло не более двух событий; 8) произошло менее двух событий.

Решение.

1. Произошел элементарный исход, благоприятствующий событию А не благоприятствующий событиям В и С. Следовательно, произошл событие ABC.

2.Произошел элементарный исход, благоприятствующий событиям

иВ и не благоприятствующий событию С. Следовательно, произошл событие ABC.

3.Произошло событие А ВС.

4.Произошел элементарный исход, благоприятствующий, по крайне мере, одному из событий: А, В или С, т.е. произошло событие (А + В + С).

5.Произошел элементарный исход, благоприятствующий ровн

одному из трех событий, т.е. произошло событие ABC + АВС+ ABC-

6.Произошло событие ABC = А + В + С-

7.Противоположное событие заключается в том, что произошли все

событий не произошло.

8. Произошел элементарный исход, благоприятствующий по крайней мере двум из трех событий; значит, можно записать, что произошло событие (АВ + ВС +AQ.

2.4.6.Событие А = {хотя бы одно из имеющихся четырех изделий бракованное}, событие В = {бракованных изделий среди них не менее двух}. Что означают события А\В, А, В? Можно ли сказать, что В с А?

Решение. Построим пространство элементарных исходов. Из условия задачи следует, что элементарным исходом в данном случае является количество бракованных изделий среди четырех данных. Тогда возможны 5 исходов. Обозначим их числами от 0 до 4; Q = {0, 1, 2, 3, 4}; А = {1, 2, 3, 4}; В = {2, 3, 4}; А\В = {1}; А = {0}; В = {0, 1}; А\В - {среди четырех изделий ровно одно бракованное}; А = {все изделия годные}; В= {среди чегырех изделий менее двух бракованных}. Событие В а А.

2.4.7.Доказать равенства: А + В = А В ; АВ = А + В.

Решение. Мы должны показать, что события А + В и А В состоят из

одних и тех же элементарных исходов. Пусть элементарный исход О) принадлежит событию А + В.

например, равенство f] А,, = £ А\

П

Пусть элементарный исход со принадлежит событию f] А,. Тогдг

Ы\

п

=> й) € О А\ . i=l

2.4.9. Доказать ложность утверждения: [А + BJC =• А + ВС (Л а ВС)-

Я с

= АСВ + ABC + ABC

Рис. 2.3 Если (Л + 0 ) С = А С + Я С , то ЛСЯ = ЛЯС = 0. Далее /1С = =

- АС(В + В) = АСВ+_АСВ, ВС = ВСП = ВС(А + А) = ВСА + ВСА. Из соотношения ЛСЯ = А ВС = 0 следует соотношение АС = ВС = ABC

22

К Л А С С И Ч Е С К О Е О П Р Е Д Е Л Е Н И Е В Е Р О Я Т Н О С Т И

3.1. Определение и простейшие свойства

Пусть пространство элементарных исходов Q состоит из п невозможных исходов. Назовем вероятностью элементарного исхода число р(со) = \1п. Итак, если у нас есть основания полагать, что (меитарные исходы эксперимента равновозможны (ни у одного из них эеимуществ перед другими в смысле возможности произойти или не 'изойти), то каждому из них мы ставим в соответствие одну и ту же >ятность - Мп. По-другому говорят так: у каждого элементарного

©да есть один шанс из п произойти.

Рассмотрим произвольное событие А. Если тА - число исходов, гоприятствующих событию А, то вероятностью события А означается р{А)) называется число

т

Очевидные свойства вероятности: р (Q) = 1 ; р(0) = 0; 0 < р(А) <, 1;

А) = 1 -р(А); если Aw В несовместны, АВ = 0, то р(А+В) =р{А) + р(В).

3 2 Теорема сложения вероятностей

Если события А и В совместны, АВ Ф 0, вероятность суммы А + В

Докажем эту формулу.

Пространство Q состоит из п элементарных исходов, событие А

и 11одсчитаем число исходов, благоприятствующих сумме А+В. Событие А+В можно представить как сумму трех несовместных собы-

• А + В = (А\АВ) + А В + (В\АВ) (рис. 3.1). В событие А\АВ входят тА-

Рис. 3.1

3.3.Задача о выборке

Пусть имеется п предметов, т из которых назовем «белыми», а остальные п - т - «черными». Из этих я предметов наудачу выбирают к штук. Найти вероятность того, что / из этих к выбранных предметов «белые» и, следовательно, к - I - «черные». Перенумеруем предметы. «Белым» припишем номера с 1 по т, а «черным» - номера с т + 1 по w. Тогда элементарный исход - это неупорядоченный набор (сочетание) из к номеров, выбранных из п имеющихся. Из условия задачи следует равновозможность всех элементарных исходов; всего же элементарных исходов С*-

Событию А = {в выборке из к предметов / штук «белых»} благоприятствуют все те элементарные исходы, которые содержат / номеров в диапазоне от 1 до т ик-l номеров в диапазоне от т - 1 до п.

По принципу умножения число таких элементарных исходов равно

тА =С'тСп-'т-

Вероятность события А равна

С' Ск~'

3.4. Примеры решения задач

3.4.1. Брошены две игральные кости. Найти вероятности следующих событий: А = {сумма выпавших очков равна 8, а модуль разности равен 4}; В = {сумма выпавших очков равна 8, если модуль разности равен 4}.

Решение. Под элементарным исходом будем понимать число очков, выпавших на каждой из костей. Из соображений симметрии следует, что

24

1кие исходы равновозможны, ни одному из них нельзя отдать |>едпочтение перед другими. Всего исходов 36 (на каждой из костей Южет выпасть любое число очков от 1 до 6, а костей две).

П = {(1, 1), (1,2),..., (1, 6),..., (6,1), (6,2),..., (6, 6)}.

Запись (/, к) означает, что на первой кости выпало / очков, а на второй к очков. Исходы, благоприятствующие событию А: А = {(2,6), (6,2)}.

(Таким образом, п = 36, т = 2,р(А) = 1/18.

Если известно, что модуль разности чисел выпавших очков равен 4, то |ространство элементарных исходов содержит уже не 36, а только 4

*хода. Q = {(1, 5), (2, 6), (5, 1), (6, 2)}.

Событию В благоприятствует два исхода: п = 4, т = 2, р(В) = 1/2.

3.4.2. В магазине имеется 180 бутылок молока, 60 из которых Гированы предыдущим числом, остальные бутылки содержат свежее локо. Покупатель выбирает наугад 6 бутылок молока. Чему равна роятность события А' = {по крайней мере две бутылки окажутся тированы предыдущим числом}?

Решение. Перед нами задача о выборке. Назовем «белыми» бутылки со ;жим молоком, «черными» - бутылки, датированные предыдущим

слом.

Найдем вероятность события А = {среди выбранных шести бутылок не лее одной «черной»}; А = А\ + Аь где А\ = {среди выбранных шести

утылок одна «черная»}, Аг = {все 6 выбранных бутылок - «белые»}.

р\А) = 1 -р(А)= 1 - С « С '» + С'620 ;о>65з,

3.4.3. В лифт семиэтажного дома вошли на первом этаже 3 человека, дый из них с одинаковой вероятностью выходит на любом из этажей,

чпная со второго. Найти вероятности следующих событий:

А = {все пассажиры выйдут на четвертом этаже}; В = {все пассажиры Идут на одном этаже}; С= {все пассажиры выйдут на разных этажах}.

Решение. Элементарный исход для этого эксперимента - номер этажа, котором выйдет каждый пассажир. Будем обозначать исходы тройкой ним: например, запись (3, 6, 4) означает, что первый пассажир вышел на

Событию А соответствует один элементарный исход: А = {(4, 4, поэтому р(А) ° 1/216.

Событию В благоприятствуют 6 элементарных исходов: В = {(2, (3, 3, 3 ) , ( 7 , 7, 7)}. Отсюда р(В) = 6/216 = 1/36.

По принципу умножения событию С благоприятствуют 6x5x4 = элементарных исходов. Поэтому р(С) = 120/216 = 5/9.

3.4.4. Имеется к шариков, которые случайным образом разбрасывав

<>|

по т лункам. Найти вероятность того, что в первую лунку упадет ровне шариков, во вторую - кг шариков и т.д., в т-ю лунку - кт шариков, если

+ к2 + ...+ кп = к.

Решение. Элементарный исход дзя этого эксперимента может бы записан как последовательность из к чисел а\, а 2 , а 1 г а * , где число 4 это номер лунки, в которую попал /-й шарик, 1 < I < к, 1 <a,<i т.

те и только те элементарные исходы, которые образуют перестаное

Вероятность события А равна

кх\к2\...кя\т'

3.4.5. Из полной колоды карт (52 листа) извлекают наудачу несколы карт. Сколько карт нужно извлечь для того, чтобы с вероятность* большей 0,5, утверждать, что среди них найдутся карты одной и той масти?

Решение. Обозначим искомое число через к. Прежде всего замети что если к > 4 , то среди выбранных карт наверняка найдутся карты О: и той же масти. Значит, нужно рассмотреть случаи, когда к = 2, 3,4.

1. * = 2, число элементарных исходов равно с|2 =1326Событие А = {две карты одной масти} есть сумма четыре

несовместных событий: А = А\ + А2 + А$ + А*, где событию А, (/ = 1, 2, 3, 4 соответствует фиксированная масть. Так как тА = С23 (выбираютс

любые две карты из 13 карт данной масти), то тА = 4 • С,23 =312Тогда/>(Л) = 312/1326 = 0,235 < 0,5.

2 к = з, п = с\2 = 22100. Найдем число исходов, входящих в событие

Чтобы выбрать три карты разных мастей, нужно сначала выбрать три рпределенные масти из четырех. А затем выбрать по одной карте из Тринадцати карт каждой из выбранных мастей.

Значит, тл = С\С\ъСхпС\ъ =8788Тогда тл = 22100 - 8788 = 13312, а вероятность события А " {есть карты одной масти} равна

Итак, нужно выбрать не меньше трех карт.

3.4.6. На выборах, в которых участвовали два кандидата, А и В, за них •оступило п и т (п < т) бюллетеней соответственно. Бюллетени извлекают ШЯ урны последовательно, один за другим. Какова вероятность того, что Хотя бы один раз число вынутых бюллетеней, поданных за А и за В, было одинаково?

Решение. Обозначим элементарный исход последовательностью из п + ш букв А и В (в ней п букв А и т букв В). Буква А на /-м месте означает, что

Например, для л = 3 и т = 2 получаем 10 последовательностей: ИВА А А. ВАВАА. ВААВА, BAAAB, ABBAA, ABABA, АВААВ, ААВВА, ААВАВ, АААВВ.

Так как п > т, ясно, что если первой буквой в последовательности

и I in.,. /•-.' и наоборот, до icx пор, пока первый МП не поменяем рапное Вркло букв А и В, Например, последовательность АВААВ превратится в щАААВ, а последовательность АВВА А перейдет в ВАВАА.

Итак, каждой последовательности, начинающейся с буквы А, в которой

достигается равенство букв А и В, соответствует последовательно начинающаяся с буквы В.

Подобным же образом любую последовательность, начинающую буквы В, можно перевести в последовательность, у которой первая бую

ив которой достигается равенство чисел букв А и В. Напри,

последовательность ВАВАА переходит в АВВАА, последовательно ВВААА переходит в А ABB А и т.д.

Установлено взаимно-однозначное соответствие между все последовательностями, начинающимися на букву В, и все! последовательностями, начинающимися на букву А, в которых достига равенство чисел букв А и В.

Пусть заданы пространство элементарных исходов Q , содержаще равновозможных элементарных исходов, событие А, содержащее исходов, событие В, содержащее тв исходов, и произведение АВ, котороТ благоприятствуют тЛВ исходов. Тогда

р(А) = mjn; р(В) - тв/п; р(АВ) = / н е ­

известно, что в результате эксперимента произошло событие А; в э* условиях нужно найти новую вероятность события В. Такая вероятно обозначается символом р(В/А) и называется условной вероятное- события В при условии, что произошло событие А.

Если произошло событие А, то произошел один из тА элементарн исходов, благоприятствующих этому событию. Следовательг пространство элементарных исходов П сузилось до события А и содерж. теперь не я, а только тА исходов. Во множестве А событию благоприятствуют исходы, входящие в произведение АВ, их количест равно тАВ, поэтому

В примере 3.4.1 определялась именно условная вероятность события Формулу (3.4) можно записать по-другому:

формула (3.5) выражает собой так называемую теорему умножения

Щлтностей.

События А и В называются независимыми тогда и только тогда, когда

В случае независимых событий А и В теорема умножения вероятностей 1И< инастся совсем просто:

]^вссмотрим такой пример. Эксперимент заключается в бросании двух н.ных костей, П = {(1,1), (1, 2), ... , (6,6)} , я = 36. События А = {на •и кости выпало четное число очков} н В = {на второй кости выпало > очков, делящееся на 3} независимы, так как тл = 18, тв = 12, тАВ = 6,

?А/2,р(В)=\/3,р{АВ)=\/6,р(АВ)=р(А)р(В)-

\ ЮГ результат соответствует интуитивным представлениям о ii нмости исхода бросания одной кости от исхода бросания другой. Г^Ьтия, которые не являются независимыми, называются

4 . А К С И О М Ы Т Е О Р И И В Е Р О Я Т Н О С Т Е Й

Рассмотрим произвольное пространство элементарных исходов £ Выделим в нем систему S подмножеств (событий) так, чтобы выполнялис следующие три условия:

о-алгеброй, когда постулируется, что сумма бесконечного числа событи принадлежит $, если каждое из слагаемых принадлежит S.

применяется п - 1 раз).

В случае о-алгебры произведение бесконечного числа событ принадлежит S, если каждый из сомножителей принадлежит S. Это следу из условий 2, 3, определения гт-алгебры и результатов задачи 2.4.8

Поставим в соответствие каждому событию A e S число р(АЦ

.2. /Ч^) =Р(А+ А) =р(А)+р(А) = 1 => р(А) = 1 -р(А) для всякого Ьггия AeS.

3. Из аксиомы 1 и следствия 2 вытекает, что вероятность любого китмя А не превосходит единицы,

0<р(А)< 1.

Н . Если Л с В , то/?(Л) < / ? ( 5 ) .

[Действительно, если А с 5, то событие 5 можно представить в виде шы двух несовместных событий: В = А+ (В\А).

Тогда согласно аксиоме 3

р(В) =р(А + В\А) = р{А) + р(В\А) > р(А), так как согласно аксиоме 1

5. Пусть события А и 5 совместны. Как и в случае классической схемы,

ество Q из п равновозможных исходов; множество всех подмножеств

то 2" событий); множество вероятностей событий, определяемых кулой р(А) = тА /п, где тА - число исходов, входящих в событие А. :сические вероятности удовлетворяют трем перечисленным аксиомам.

4.2.1. Конечное число неравновозможных исходов

Множество Q содержит п неравновозможных элементарных исходов. Х>н i мости picOj) , 1 <, i < п задаются тем или иным образом так, чтобы не |>ша 11, аксиомы 1 - 3 . Таким образомр(со,) > 0; кроме того,

£рМ=р(П)=\.

/=1

Алгебра событий S содержит все подмножества Q, всего 2" событий; оятность любого события А равна (по аксиоме 3) сумме вероятностей ментарных исходов, благоприятствующих событию А.

со,еА

4.2.2. Счетное множество неравновозможных исходов

Множество Q счетное, элементарные исходы ш, (i = 1, 2, 3,...) неравн возможны. Вероятности р{ш,) должны удовлетворять аксиомам 1 -

ос

Следовательно, р(а),) > О, р(С1) = £ Р(о>,) = 1 •

/=1

оалгебра событий S содержит все подмножества пространства вероятность любого события А равна сумме (быть может, бесконечно вероятностей элементарных исходов, входящих в А.

р(А)= ЕЩщ) ai,cA

Сходимость бесконечного ряда вытекает из сходимости ряда

И

4.2.3.Геометрические вероятности

Вкачестве пространства элементарных исходов Q возьмем множеств точек прямой, плоскости или пространства, имеющее конечную длина площадь, объем соответственно. Событиями назовем любые подмножеств О, также имеющие конечную длину, площадь, объем (возможно, равны; нулю).

Вероятность события А определим формулой

Так определенное правило вычисления вероятности события означас^ что вероятность некоторого события зависит только от значения его длин (площади, объема) и не зависит от других факторов. Таких, например, к форма события, его положение внутри О, связность и т.п. Элементарны исходы - это точки прямой (плоскости, пространства). Так как щш (площадь, объем) точки равны нулю, вероятность каждого элементарног исхода равна нулю. Пользоваться формулой геометрической вероятное! при решении некоторой задачи можно, если условие задачи позволя допустить, что события, имеющие равные длины (площади, объемы равновероятны.

32

»тры? Регулярно ли вы смотрите телевизионные передачи? жзалось, что 40 % опрошенных регулярно посещают кинотеатры и

•{респондент смотрит телевизор}. Событию А благоприятствуют два Нкода: А = {КТ, КТ} . Событию В тоже благоприятствуют два исхода: В = Щ§С1, К Т) . Вероятность события А равна сумме вероятностей входящих НРЕГО элементарных исходов: р(А) = 0,4 + 0,2 = 0,6. Тогда р{ А) = 1 - 0,6 =

• М . Аналогично р(В) - 0,4 + 0,3 = 0,7; />( В) = \ - 0,7 = 0,3.

| Нужно найти вероятность события А + В. Это можно сделать «в лоб» - ^ В ы т и е А + В - это множество {КТ, К Т, КТ } , поэтому р(А + В) = 0,4 + •0,3 +• 0,2 = 0,9. Можно воспользоваться формулой р(А+В) = р(А) +р(В) - I /ААВ). Произведение АВ содержит один элементарный исход {КТ},

Ьэтому р(АВ) = 0,4, тогда р(А +В) = 0,6 + 0,7 - 0,4 = 0,9.

Можно перейти к вероятности противоположного события:

I Вероятность того, что пассажиру придется ждать поезда не более чем 30 с,

33

если поезд стоит 30 с?

Решение. В данном случае множество ft состоит из точек отрезка (время выражено в минутах). Предполагается, что можно воспользова схемой геометрических вероятностей. Событие А = {время ожид~ поезда не превосходит тридцати секунд} состоит из точек отрезка [0; 0 11,5; 2].

Вероятность события А равна р(А) = 1 / 2.

4.3.3.В круге наудачу выбирается хорда. Найти вероятность того,

еедлина не превзойдет длины радиуса круга.

Решение. Как уже было замечено (пример 2.4.4), можно построит крайней мере три различных пространства элементарных исходов этого эксперимента. В каждом из этих случаев предполага применимость формулы геометрических вероятностей.

1. Хорда определяется случайным выбором точки В на окружи

ОС = ylR2-R2/4 = RJ0J5.

Длина хорды не более R, когда середина хорды удалена от центра расстояние ОС > Л-^0,75. Таким образом, событие А =• {центр хор удален от центра круга на расстояние, не меньшее R*jQ,75 }, содержит точки кольца, ограниченного окружностями радиусов R и R Площадь этого кольца равна

л/?2 - 0,75лЛ2 = 0,25л/?2, р(А) = 0,25лЛ2/л/?2 = 0,25.

3. Расстояние от центра круга до хорды - наудачу выбранное число отрезка [0, R]. Множество ft - это множество точек отрезка [0; Событию А = {центр круга удален от центра хорды на расстояние,

и разных ответа - 0,33, 0,25, 0,134 все верны, потому что эти ответы тся к разным задачам. При решении любой задачи (не только по и вероятностей) нужно стараться ясно и недвусмысленно описать, Именно дано и что требуется определить. Только в этом случае можно

п, о правильности решения или об ошибке в рассуждениях.

= p(AIC)p(BIAC)*p(A/C)p(B/C), ведь множества ВIС и В/А

общем случае состоят из разных элементарных исходов и, следовател имеют разные вероятности.

В качестве примера рассмотрим эксперимент с бросанием кубиков. Пусть событие А = {на первом кубике выпало четное чя| очков}; событие В = {на втором кубике выпало нечетное число очк, событие С = {сумма выпавших очков равна числу 6}. Тогда события А независимы. При этом

р(А/С) = 2/5; р(В/С) = 3/5; р(В/АС) = 0 * 6 / 2 5 .

5.2. Примеры решения задач

5.2.1. Известно, что вероятность рождения мальчика равна вероятн рождения девочки и равна 0,5. В семье двое детей, из них один ребен мальчик. Какова вероятность того, что и другой ребенок тоже маль, если дети рождаются независимо друг от друга?

Предлагаются два ответа:

1.Искомая вероятность равна 0,5.

2.Если известно, что один из детей - мальчик, то получаются равновозможных исхода: {ММ, МД, ДМ}, где исход ДМ, напри означает, что первый ребенок - девочка, а второй - мальчик. Та искомая вероятность равна 1/3.

Какой из ответов правильный?

Решение. Правильны оба ответа, потому что они относятся к разн экспериментам. Первый эксперимент - случайный выбор ребенка! множества детей, принадлежащих семьям с двумя детьми. Отмечае брал или сестра у выбранного ребенка. Тогда пространство элементар" исходов состоит из четырех равновозможных исходов:

П={М(б),М(с),Д(б),Д(с)}.

Исход М(б) означает, что выбран мальчик и у него есть брат. Ис" Д(с) означает, что выбрана девочка и у нее есть сестра. По условию зад вероятность события В ={выбран мальчик} = {М(б), М(с)} равна чи 0,5. Вероятность события С = {у выбранного ребенка брат} = {М(б), Д£

Второй эксперимент - случайный выбор семьи из множества семе двумя детьми. Элементарный исход - пол каждого из детей. Здесь си четыре равновозможных элементарных исхода {ММ, МД, ДМ,

ность события В ={в выбранной семье есть по крайней мере один ,ик} равна 3 / 4.

усть событие С = {в семье два мальчика}. Тогда ВС = С и р(ВС) =

• 0,25. Далее

доживший до 20 лет, доживет до 60?

Вцение. Построим пространство элементарных исходов. Эксперимент •Дается в выборе случайного человека и фиксировании длительности »н щи. Имеем всего три исхода: Q = ^0, 2060 ,6о|. Обозначение " 2 0 " JiBci. что человек не дожил до 20 лет, обозначение "2060" - что он Шло 20 лет, но не дожил до 60, обозначение "60" означает, что дожил до 60 лет. Событие А = {человек дожил до 60 лет} влечет {человек дожил до 20 лет}. По условию р(А) = р2,р(В) = р\.

В) = р2/р].

Анна и Бригитта - две маленькие девочки-близнецы. Они похожи руга как две капли воды. В школе они сидят на одной парте, одна дится слева, а другая - справа. Каждая из них утверждает, что она

. Учительница из опыта знает, что, вообще говоря, девочка справа н раз из четырех, а девочка слева - один раз из пяти. Учительницу ет, чему равна вероятность того, что Анна сидит слева. Помогите

цие. Элементарный исход здесь - информация о том, лжет или правду девочка, сидящая слева, и девочка, сидящая справа. Тогда гтыре исхода: {ЛЛ, ЛП, ПЛ, ПП}. Буква П означает, что гвующая девочка говорит правду, а буква Л означает ложь,

в другая лжет. Нужно найти вероятность того, что девочка слева иачит, девочка справа говорит правду, т.е. условную вероятность