862

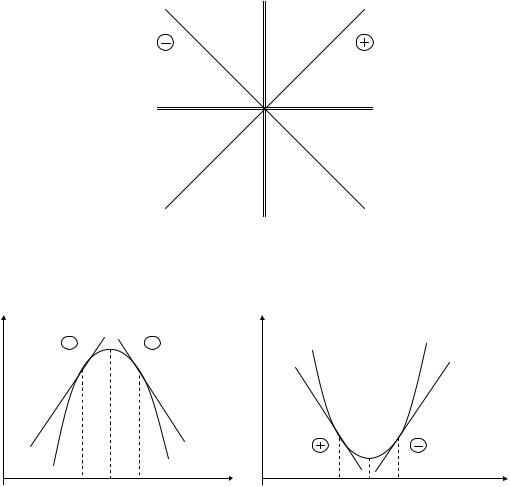
следует заметить, что если касательная проходит через первый и третий квадранты, то она положительная, а если через II и IV – отрицательная, как показано на рис. 11.

Рис. 11. Геометрическая интерпретация определения знака первой производной от рассматриваемой функции

Рис.12. Второе достаточное условие существования экстремума одномерных функций

Для определения типа экстремума используют следующее правило: если при переходе через “подозрительную” на экстремум точку первая производная меняет свой знак с плюса на минус, то в рассматриваемой точке x=x0 существует локальный максимум, как показано на рис. 12, а, и

50

имеет минимум, если наблюдается обратное чередование знаков первой производной при переходе “стационарной” точки (рис. 12, б). Если проще вычислить более высокие частные производные то применяют третье достаточное условие.

3. Если вторая производная в “подозрительной” на экстремум точке x=x0 имеет знак плюс, то в рассматриваемой точке x=x0 существует локальный минимум (рис. 13, а), а если эта величина отрицательная, т.е. имеет знак минус, то – локальный максимум (рис.13, б). В обобщенном виде это правило формулируется следующим образом: если первая отличающаяся от нуля производная нечетная, т.е. первая, третья, пятая и т.д., то в рассматриваемой точке экстремума нет, а если эта производная четная, то в рассматриваемой точке максимум, если она отрицательная, и минимум при её положительном значении.

Рис. 13. Третье достаточное условие существования экстремума одномерной функции

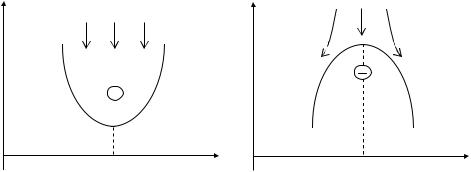
Для более прочного запоминания этого правила целесообразно привести следующий механический аналог: если на пути вертикального потока дождя встречается вогнутая поверхность, то в ней вода накапливается и её присутствие в емкости можно обозначить знаком плюс, а если при прочих равных условиях капли дождя попадают на выпуклую поверхность, то они с неё скатываются, не задерживаясь на поверхности.

Этот факт – отсутствие воды на поверхности емкости, ориентированной выпуклостью вверх, – можно условно обозначить знаком минус. На основе этой аналогии третье достаточное условие

51

экстремальности одномерных функций получило название “правило дождя”.

4.3. Необходимые и достаточные условия существования экстремумов многомерных функций

Необходимым условием существования экстремума многомерных функций является равенство нулю её частных производных, т.е.

Для того чтобы определить, существуют ли в стационарных точках экстремумы, используют матрицу Гесса – матрицу, составленную из вторых смешанных частных производных рассматриваемой функции, которая в общем виде записывается следующим образом:

Определяющими здесь служат главные миноры матрицы Гесса. Главным минором матрицы называется определитель, составленный из К первых строк. Допустим, матрица

Если главные миноры матрицы Гесса имеют чередующиеся знаки с минуса на плюс, то в рассматриваемой точке – локальный максимум, если главные миноры положительны, то в

52

рассматриваемой точке – минимум.

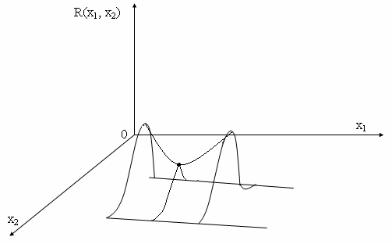
Если знаки главных миноров чередуются с плюса на минус, то в рассматриваемой точке располагается седло, как показано на рис. 14. Причем, по оси Х1 имеем минимум, а по оси Х2 – максимум. Если же чередование знаков главных миноров матрицы Гесса отличается от указанных, то в рассматриваемой точке нет экстремума.

Рис. 14. Геометрическая интерпретация седловой точки

4.4. Метод неопределенных множителей Лагранжа

Пусть задана функция цели

Необходимо определить экстремум функции цели (46) в рамках следующих ограничений:

Необходимо определить значения неизвестных xi, при которых целевая функция достигает экстремума. Подобная задача встречается в инженерной практике при распределении исходных ресурсов по производствам. Задача определения экстремума функции (46) при условии выполнения системы ограничений (47), заданных в виде равенств, называется задачей на условный экстремум.

Если через n обозначить число неизвестных системы (46) – (47), а через m – количество ограничений (47), то их разность n-т дает так называемую степень свободы решаемой задачи. Обычно в подобных случаях n > m и решение осуществляют в такой последовательности.

Первые m неизвестных выражают через n-т остальных неизвестных, иначе

xm 1,xm 2,...,xn.

После чего оптимальное значение этих неизвестных подставляют в соотношение (47) и определяют остальные m неизвестных. Таким образом, задача решена.

В действительности на практике часто бывает невозможно выразить m первых неизвестных через остальные, т.е. получить соотношение (48). Потому задача на условный экстремум решается с использованием метода множителей Лагранжа, сущность которого сводится к следующему.

Пусть будет задана целевая функция

Здесь используют следующий прием: задача на условный экстремум сводится к классической за счет суммирования всех ограничений, умноженных на соответствующие коэффициенты, с функцией цели, т.е.

L(x) R(x1x2,...,xi ,....,xn ) j bj qj (x1x2 ,...xn ) max(min).(51)

j

Как видно из соотношения (51), функция цели от этой операции не изменяется, поскольку с ней суммируются нулевые члены, умноженные на соответствующие коэффициенты. Вновь вводимые коэффициенты называются множителями Лагранжа. Функция, приведенная в формуле (51), называется функцией Лагранжа.

54

Далее задача решается классическим методом, т.е. определяем первую производную от рассматриваемой функции по всем неизвестным и по всем множителям Лагранжа:

В результате решения системы уравнений (52) находим “подозрительные” на экстремум или “стационарные” точки. Число уравнений в системе (52) будет m+n неизвестных, из которых определяют неизвестные хi и не определяют множители Лагранжа, если в этом нет необходимости.

Вид экстремума определяется на основе достаточных условий. Множители Лагранжа показывают чувствительность функции цели к константам ограничений, т.е. j имеет выражение

Вэтом соотношении выражается интерпретация множителя Лагранжа. Исходя из этого, если j =0, это значит, что bj не оказывает существенного влияния на функцию цели. Чем больше j, тем больше j-я константа влияет на целевую функцию.

Впрактике решения задач методом неопределенных множителей Лагранжа принята такая последовательность:

1. Ограничения (50) приводятся к виду, имеющему 0 справа.

2. Составляется функция Лагранжа. При этом на каждое ограничение вводится по множителю Лагранжа.

3. Берут частные производные по всем неизвестным и всем множителям от функции Лагранжа, в результате чего получают m+n уравнений. Решая совместно m+n уравнений, определяют оптимальные величины неизвестных, после чего задача считается решенной.

Чаще всего этим методом решаются производственные задачи в рамках ограничений в виде равенств, также его используют при определении оптимальных геометрических размеров фигур.

55

4.5. Типовой расчет «Аналитические методы поиска экстремума»

4.5.1. Задание

Используя исходные данные для заданного варианта, помещенные в прил. 3, необходимо:

1. Определить экстремум следующей одномерной функции:

(величины констант a1 a8 указаны в прил. 3, столбцы 2–9). Всего приведен 31 вариант заданий.

2. Определить экстремум следующей многомерной функции

3. Из квадратного листа жести размером b5 (в метрах) изготовить емкость максимального объема в виде бака прямоугольной формы без крышки. При этом b5=30 +N+6, где N – порядковый номер студента в списке группы; – последняя цифра номера группы.

4.5.2. Образец выполнения работы

Текст задания записать в соответствии с подразд. 4.5.1 в отчет. Числовые значения по заданному варианту (см. прил. 3) свести в табл. 7. Рассмотрим выполнение настоящей работы по варианту 31 со следующими исходными данными.

По образцу функции (В) составляем одномерную функцию. Согласно заданию имеем

R(x) 2x3 48x2 .

Таблица 7

Исходные данные

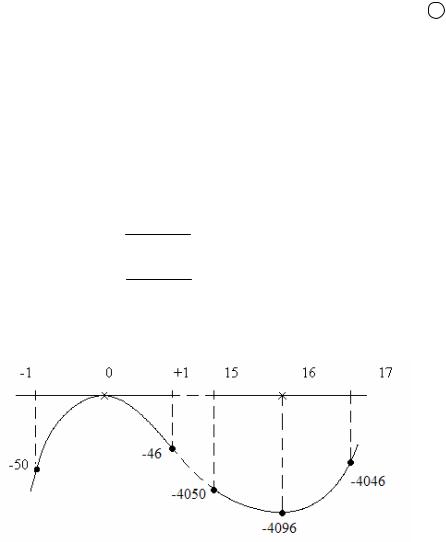
Определяем R'(x) 6x2 96x 0, отсюда x(6x–96)=0, тогда x1=0 первая точка, "подозрительная" на экстремум. Исследуем - окрестность точки x1=0. Определяем характер экстремума по первому достаточному условию существования экстремума одномерных функций. Для этого окружаем точку x1 0 -окрестностью, равной 1. Подставляем значения x1=0; x1=+1 и x1=–1 в целевую функцию (В), имеем

локальный максимум. Проверяем характер экстремума в точке x1=0 по второму достаточному условию экстремальности одномерных функций. Берем = 1 и

R'(x1 ) R'( 1); R'(x1 ) R'( 1).

Производим вычисления

R'( 1) 6( 1)2 96( 1) 102; R'( 1) 6( 1)2 96( 1) 90.

Поскольку при переходе через "подозрительную" точку x1=0 первая производная изменяет знак с плюса на минус, то в рассматриваемой точке имеем максимум.

Проверим по "правилу дождя". Это третье достаточное условие существования экстремума одномерных функций. Для этого возьмем вторую производную от заданной функции R"(x) 12x 96. При x1=0 имеем R"(x1) 96. Поскольку производная четная и отрицательная, то в рассматриваемой точке существует локальный максимум, т.е. выводы всех трех проверок совпадают. Таким образом, в первой точке x1=0 существует максимум.

Определяем вторую точку, "подозрительную" на экстремум: 6x=96. Отсюда x2=16.

Исследуем по вышеизложенной методике теперь уже без дополнительных пояснений эту точку:

I. Выбираем единичную -окрестность.

R(16–1)= 4050; R(16)= 4096; R(16+1)= 4046.

Поскольку в точке, "подозрительной" на экстремум (x2=16),

57

величина целевой функции (B) меньше, чем в (x2 )=(16 1), то в точке x2=16 существует локальный минимум.

II. R'(15)= 90; R'(17)=+102.

Поскольку при переходе через точку x2=16 первая производная меняет знак с 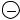на 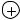, то в точке x2=16 существует локальный минимум.

III. R''(x)=12x; R''(x2=16)=192.

Поскольку вторая производная в рассматриваемой точке имеет знак, то в точке x2=16 существует локальный минимум.

Проверки по всем трем достаточным условиям для точки x2=16 совпали. Отчет о работе необходимо сопроводить примерным графиком рассматриваемой функции, как показано на рис. 15.

Составляем многомерную функцию на основе задания:

Определяем первые частные производные по переменным x1 и x2 и приравниваем их к нулю:

R(x1,x2) 2x2 4 6x1 0;

x1

R(x1,x2) 2x1 8 8x2 0.

x2

Рис. 15. Геометрическая интерпретация экстремумов рассматриваемой функции в точках x1=0 и x2=16

Решаем систему.

Вычитаем из первого уравнения второе

58

Точка с координатами х1=4/11 и х2=10/11 “подозрительная” на экстремум. Для уточнения вида экстремума воспользуемся достаточным условием существования экстремума многомерных функций.

С этой целью вычисляем вторые смешанные частные производные:

На этой основе составляем матрицу Гесса по аналогии с матрицей (43)

Вычисляем главные миноры матрица Гесса по формуле (45): M1 6; M2 44. Поскольку главные миноры матрицы Гесса

меняют знак с минуса на плюс, то в рассматриваемых точках x1 4 и 11

x2 10 имеем локальный максимум.

11

Определение оптимальных размеров бака. Решение задачи начинаем с раскроя предложенного листа жести размером 4 4 м. (см. табл. 7, столбец b5 ) на предмет получения заготовки будущего бака прямоугольной формы без крышки, как показано на рис. 16. Целью решения задачи является получение максимального объема будущего бака.

59