862

Отсюда

х22 = 1,9 – 0,02 9,6 = 1,708.

7.Вычисляем величину целевой функции на 2-м шаге при х12=2

их22=1,708.

R(xi) 22 2 (1,708)2 2 1,708 13,25.

8. Сопоставляя величины целевой функции в точке, откуда шагали (15,02), с точкой, куда шагали (13,25), делаем вывод о том, что шаг оказался удачным.

Теперь по рассмотренному алгоритму продолжаем движение до тех пор, пока функция будет уменьшаться (т.е. изменяться желательным образом), а результаты этих расчетов для краткости изложения материала заносим в табл. 5.

Таким образом, удваивая фактор шага, дошли до 7-го шага, когда целевая функция возросла (3,579). Шаг оказался неудачным. Условимся неудачные шаги обозначать со штрихом (этот шаг будет 7'), чтобы отличить их от шагов удачных. Последним удачным был 6- й шаг (х16 = 2; х26 = –0,627). Уменьшаем фактор шага в два раза (вместо 0,64 берем 0,32) и осуществляем очередной шаг из 6-й точки.

Имеем х17 = 2; х27 = –0,464; R(xi) = 3,502. На 6-м шаге R(x) = 3,532. Это значит, что шаг оказался удачным. Обозначаем его как шаг 7 и продолжаем движение. Уменьшаем фактор шага еще в два раза (0,16) и осуществляем очередную попытку движения из 7-й точки (х18=2; х28=–0,484). При этом целевая функция равна 3,5, а в 7-й точке R(xi)=3,502. Значит, шаг удачный. Уменьшаем еще в два раза фактор шага (0,08) и осуществляем движение из последней (8-й) удачной точки. Девятая точка будет иметь координаты х19 = 2; х29 = –0,489

R(2; –0,489) = 3,5, R(2; –0,489) = 3,5. Целевая функция не ухудшилась. Как видно из результатов расчетов (см. табл. 5), последующее уменьшение фактора шага в два раза (0,04) не дало желаемого результата – функция по сравнению с точкой 9 (3,5) не уменьшилась (3,5). Поэтому определяем частные производные по осям, чтобы выбрать новое направление движения в последней удачной точке – точке 10 (2; –0,49).

40

Окончание таблицы 5

Наибольшая производная — по оси х1 (3,51), поэтому выбираем новое направление движения по координате х1, а х2 фиксируем на уровне –0,49 и продолжаем вычисления.

R(1,965; -0,49) = 3,379.

Поскольку на 10-м шаге R(x1)=3,5, то шаг оказался удачным. Удваивая фактор шага, мы доходим до шага 18, при котором исследуемая функция увеличилась по сравнению с предыдущим (17- м) шагом (0,439>0,427). Обозначаем неудачный шаг номером 18', уменьшаем фактор шага вдвое (вместо 1,28 берем 0,64) и продолжаем движение из последней удачной точки (т. 17). Шаг оказался удачным (0,427>0,422). Из точки 18 осуществляем 19 и 20-й шаги с фактором шага 0,02 и 0,01 соответственно. Поскольку шаги 19 и 20 дали одинаковые отклики (0,421), а фактор шага 20 был равен заданной точности поиска (0,01), то в точке 20 вновь определяем частные производные по осям координат:

R(xi ) 2 x1 x2 2 0,206 ( 0,49) 0,078;

x1

R(xi) 4 x2 x1 4 ( 0,49) 0,206 1,754.

x2

На этом основании фиксируем координату х1=0,206 и продолжаем движение из точки 20 с фактором шага h= =0,01, который удваиваем на каждом шаге. Доходим до 26-го шага, затем уменьшаем фактор шага, начиная с 27-го шага до 30-го. Точки 27, 28, 29 и 30 имеют одинаковые отклики (0,037) при факторе шага в точке

30h= =0,01.

Вточке 30 вновь определяем частные производные по осям:

42

R(xi ) 2 x1 x2 2 0,206 ( 0,043) 0,369;

x1

R(xi ) 4 x2 x1 4 ( 0,043) 0,206 0,034.

x2

Считаем точку реверса (т. 30) как неудачную, присваиваем ей номер 30' и движемся далее, вначале увеличивая, а с 35-го шага уменьшая фактор шага. Последний удачный шаг 36, R(xi)=0,0012. Изменение фактора шага и направления движения (шаги 37', 37'', 38') не дает желаемого результата, поэтому в качестве решения принимается последняя удачная точка (точка 36).

Ответ: R(0,028 0,01; -0,024 0,01)=0,0012.

Метод крутого восхождения.

Сущность этого метода сводится к следующему.

1. Вычисляем величины первой производной по осям в исходной точке, т.е. при х10 = х20 = 2 (см. табл. 6).

2. Вычисляем соотношение первых производных по осям

приближения к оптимуму величины производных будут уменьшаться, а поэтому будем уменьшать шаги поиска), тогда х1 = 0,5 0,6 0,3.

4. Осуществляем первый шаг, т.е. вычисляем координаты

x11 и x12 ;

43

Таблица 6

Результаты расчетов методом наискорейшего спуска (подъема)

На этой основе приращения по осям принимаем равными, т.е. х1=Δх2=0,05, и продолжаем движение из точки [х18, х28], занося результаты вычислений в табл. 6. Согласно табл. 6 очевидно, что следующий неудачный шаг – шаг 13.

Вычисляем первые производные в последней удачной точке (точке 12)

тогда х1=0,01 и продолжаем движение (см. табл. 6.) На шаге 15 функция возросла (0,0296>0,0044). Определяем вновь частные производные в точке 14 по осям координат.

R(xi ) 2 x1 x2 2 0,07 0,01 0,13;

x1

R(xi ) 2 x2 x1 4 ( 0,01) 0,07 0,03.

x2

Соотношение производных 13:3. Принимаем х1=0,01, тогда Δx2 0,01 313 0,002. Поскольку обе производные положительные, то

х1 и х2 будут вычитаться из соответствующих координат. Поскольку наибольший шаг поиска равен заданной точности поиска, т.е. х2=0,01= , продолжаем движение до локального минимума, т.е. до возрастания целевой функции, и предыдущую удачную точку считаем решением задачи.

На шаге 20 наблюдается увеличение функции при поиске минимума. Поэтому оптимальным решением считаем точку

x119min 0,02; x192min 0,02; Rmin (x119;x192 ) 0,0008.

Используя формулу (37), запишем ответ.

Ответ: R(0,02 0,01;-0,02 0,01) = 0,0008.

Вопросы для самоконтроля

1.Дайте понятие градиента.

2.Сформулируйте метод градиента.

3.Что такое метод релаксаций?

4.Сформулируйте метод крутого восхождения.

46

Глава 4. АНАЛИТИЧЕСКИЕ МЕТОДЫ ПОИСКА ЭКСТРЕМУМА

4.1. Состав аналитических методов

Основным условием использования аналитических методов оптимизации является задание функции в аналитическом виде и её дифференцируемость. Существуют несколько методов отыскания экстремумов аналитических функций, в частности:

1.Методы, основанные на классическом математическом

анализе.

2.Метод множителей Лагранжа.

3.Вариационные методы.

4.Принцип максимума Понтрягина.

У каждого из этих методов есть свои условия применения. Скажем, методы, основанные на классическом математическом анализе, предполагают наличие дифференцируемости функции. Если ограничения задачи заданы в виде равенств, то используется метод неопределенных множителей Лагранжа. Вариационные методы применяются в тех случаях, когда функция цели задана в виде функционала, в частности, при решении уравнений Эйлера. Принцип максимума Понтрягина разработан сравнительно недавно группой российских ученых во главе с академиком Понтрягиным (1958 г.), но уже нашел широкое применение как у нас в стране, так и за рубежом, особенно при решении задач управления. Здесь особо следует отметить то обстоятельство, что аналитические методы связаны с большим объемом вычислений. Поэтому на пути их применения стоит барьер многомерности. Кроме того, значительное увеличение объема вычислений связано с использованием ограничений. Практически эти методы применяются для двух-трех переменных при небольшом числе ограничений.

4.2. Необходимые и достаточные условия существования экстремумов одномерных функций

В основе этих методов лежит классическое учение математического анализа об экстремумах функций. Принято понимать, что функция R(х), определенная на участке [a,b], имеет в

47

точке х=х0 максимум или минимум, а в самом общем случае – экстремумпредельное значение, если её можно окружить-окрестностью, заключенной в рассматриваемый отрезок [a,b] таким образом, что

для всех случаев, где х x0.

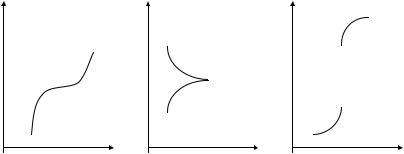
В таком случае (38) определяет минимум функции (m), а (39) - максимум (М). Существуют условия определения экстремума одномерных функций. Необходимым условием существования экстремума функции одной переменной является равенство нулю либо отсутствие её первой производной. Это условие действительно является необходимым, но не достаточным. Возможны случаи, когда это условие выполняется, а тем не менее функция не имеет ни максимума, ни минимума. В подтверждение этого на рис. 9 приведены случаи, когда необходимые условия выполняются, однако экстремум отсутствует.

Рис. 9. Геометрическая интерпретация частных случаев выполнения необходимых условий существования экстремума одномерной функции и его фактическое отсутствие

На рис. 9, а,б производные функции в точках х=x0 равны нулю, а экстремума однако в этих точках не существует, поскольку это точки перегиба кривых, изображающих рассматриваемые функции. В точке

48

х=x0 на рис. 9, в производная функции не существует, но экстремума здесь тоже нет.

Таким образом, необходимые условия существования экстремума функции используются для определения так называемых “подозрительных” или стационарных точек. Для того чтобы определить, существует ли в “подозрительной” точке экстремум и какой именно, т.е. максимум или минимум, необходимо воспользоваться одним из трех достаточных условий существования экстремума.

Достаточные условия существования экстремума функции для одной переменной следующие:

1. Если рассматриваемую точку окружить -окрестностью, такой,

что

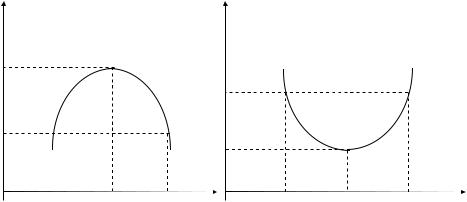
то в данной точке существует локальный максимум, как показано на рис. 10, а, а если

Рис. 10. Первое достаточное условие существования экстремума одномерных функций

Когда проще вычислить первую производную, чем функцию, то применяют второе достаточное условие существования экстремума.

2. Если при переходе стационарной точки первая производная изменяет свой знак, то в данной точке существует экстремум. Здесь

49