862

2.1.4. Метод с использованием чисел Фибоначчи

Последовательность чисел, подчиняющаяся рекуррентному

называется последовательностью чисел Фибоначчи. Другими словами, каждое последующее число Фибоначчи равно сумме двух предыдущих чисел. При этом нулевое число Фибоначчи равно единице, т.е.

рассматриваемой функции методом с использованием чисел Фибоначчи, заключающаяся в выполнении таких операций (методика расчета).

Таблица 1

Последовательность чисел Фибоначчи

1. Определяется вспомогательное число N по заданной точности поиска и диапазону исследования (Xmax Xmin ), которое рассчитывается по формуле

2. Из последовательности чисел Фибоначчи (см. табл. 1) находят такое, чтобы

4. Определяется первая искомая координата

X1 Xmin hmin FS 2 . (25)

Вычисляется значение целевой функции для точек Хmin и Х1. Пошаговая процедура в этом методе сводится к следующему:

20

определяем координату новой точки, затем вычисляем величины целевой функции в точке, откуда шагаем, и в точке, куда шагаем, которые сравниваем между собой. Если функция улучшилась, т.е. увеличилась при поиске максимума либо уменьшилась при определении минимума, то следующий шаг осуществляют из последней удачной точки в том же направлении, иначе говоря, в направлении последнего шага, уменьшая число Фибоначчи на единицу. Допустим, если на предыдущем шаге использовали F7=21, то на текущем шаге будет F6=13. Если же предыдущий шаг оказался неудачным, т.е. целевая функция в новой точке не улучшилась, то следующий шаг осуществляется из последней удачной точки (т.е. из той точки, из которой осуществляли шаг), но в сторону, обратную предыдущему шагу. Исключение здесь составляет лишь тот случай, когда мы шагаем из точки Хmin (т.е. из крайней левой точки) и шаг оказался неудачным. По изложенному правилу мы должны бы на следующем шаге переместиться влево от точки Хmin, т.е. за пределы рассматриваемого отрезка Хmin–Хmax. Поэтому в этом случае движение осуществляется из точки Хmin в направлении предыдущего шага (т.е. вправо от точки Хmin).

Возвращаясь к рассматриваемому примеру, получим (рис. 8) R(Xmin)<R(X1). Поскольку здесь определяется минимум целевой функции, то шаг оказался неудачным. Но в этом случае следующий шаг мы будем делать также вправо из точки Хmin, уменьшив номер числа Фибоначчи на единицу.

5. Производится вычисление второй координаты:

X2 Xmin h FS 3. (26)

Вычисляется значение целевой функции R(Х2).

Шаг выбран удачно, т.к. R(Х2)<R(Хmin) при поиске min, поэтому осуществляют третий шаг, рассчитывая соответствующую координату по формуле

Если бы предыдущий шаг оказался неудачным, т.е. R(Х2)>R(Х1) при поиске min, то третий шаг осуществлялся бы из исходного положения в обратную сторону, т.е.

x3 x2 hmin FS 5 . (28)

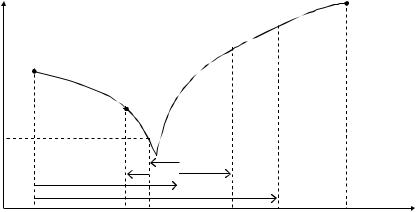
Шаговая процедура продолжается до тех пор, пока не будут исчерпаны в убывающей последовательности все числа Фибоначчи. Геометрическая интерпретация этого метода приведена на рис. 8.

Данный метод обеспечивает следующую точность поиска:

21

где FS – выбранное число Фибоначчи.

Для того чтобы можно было сравнить рассматриваемые методы по точности поиска, принимаем S=21. Тогда точность поиска составит

R(x)

R(x1)

R(x3)

R(xmin)

R(x2)

R(x4)

Рис. 8. Геометрическая интерпретация метода с использованием чисел Фибоначчи

Из этого следует, что метод с использованием чисел Фибоначчи обеспечивает наибольшую среди рассматриваемых методов точность поиска.

2.2 Безградиентные методы поиска экстремума многомерных функций

Безградиентные методы поиска экстремума многомерных функций подразделяются на методы детерминированного и случайного поиска. Детерминированные методы поиска экстремумов многомерных функций базируются на том, что всю интересующую нас область покрывают сеткой, допустим, разбивают по методу

22

сканирования с шагом (заданная точность поиска), а затем в узловых точках сетки определяют величины откликов и из них выбирают наилучший по заданному критерию.

При использовании случайных методов поиска экстремумов многомерных функций в исходной точке поиска направления пробных движений выбирают случайно; если шаг оказался удачным, то из последней удачной точки вновь выбирают случайное направление и продолжают движение. Несколько более успешным является метод случайных направлений с обратным шагом. Здесь, если случайным образом выбранное направление движения в исходной точке оказалось неудачным, следующий шаг осуществляется из последней удачной точки, но в сторону, обратную предыдущему неудачному шагу, который должен указать удачное направление поиска.

Расчеты с использованием любого из этих методов заканчиваются, если шаг поиска будет равен заданной точности поиска по осям и очередные пробные движения по всем осям не приводят к успеху. Тогда последняя удачная точка является решением задачи.

2.3. Типовой расчет "Безградиентные методы поиска экстремума одномерных функций"

2.3.1. Задание

Допустим, в результате исследования объекта получена следующая функция в общем виде

Используя исходные данные (прил. 1), где заданы коэффициенты a, b, с, d (столбцы 2–5) для 31 различного варианта, необходимо:

1.Определить экстремум функции (30) методом с использования чисел Фибоначчи для указанного варианта с заданной точностью поиска в заданном диапазоне xmin xmax (см. столбцы 6 – 7).

2.Определить экстремум функции (30) (см. столбцы 2 – 5) методами сканирования, локализации экстремума и золотого сечения (см. столбец 9) в указанном диапазоне xmin ,xmax (см. столбцы 6 – 7) с предложенной точностью поиска (см. столбец 8).

23

2.3.2. Образец выполнения работы

Текст задания записать в соответствии с подразд. 2.3.1 в отчет. Числовые значения по заданному варианту свести в табл. 2. Для примера рассмотрим выполнение настоящей работы по варианту 31 со следующими исходными данными (см. табл. 2).

На основе исходных данных (см. табл. 2) и формулы (30) имеем исходную функцию

R(x) 10x4 8x3 19x min, 4 x

которую необходимо согласно заданию исследовать на минимум четырьмя методами.

1. Метод с использованием чисел Фибоначчи.

Решение задачи методом с использованием чисел Фибоначчи осуществляем в такой последовательности:

1.1.Вычисляем вспомогательное число N согласно (22):

N xmax xmin 2,0 20.

0,1

1.2.Из последовательности чисел Фибоначчи, которую создайте сами, определяем число S, соответствующее величине N по соотношению (23). Имеем S 7; F7 21.

1.3.Определяем минимальный шаг поиска согласно (24):

h xmax xmin 2,0 0,1.

FS 21

1.4.Определяем первую искомую координату согласно (25): x1 xmin h FS 2 0 0,1 8 0,8.

Вычисляем R(0,8) 10(0,8)4 8 (0,8)3 19 0,8 12,38. Поскольку 4 0,8

R(xmin ) R(0) 0, то шаг сделан удачным, так как величина функции уменьшилась при перемещении из точки xmin в точку x1, т.е.

0> –12,38.

24

1.5.Определяем вторую координату по формуле (26), двигаясь в том же направлении:

x2 x1 h FS 3 0,8 0,1 5 1,3; R(1,3) 2,65.

Шаг сделан неудачно, поскольку R(x2) R(x1), т.е. –2,65 > – 12,38, следовательно, третий шаг будет осуществлен из последней удачной точки x1 в направлении, обратном ко второму шагу, т.е. справа налево.

1.6.Третью координату определяем по формуле x3 x1 h FS 4 0,8 0,1 3 0,5;

R(0,5) 9,16; R(0,5) R(0,8), т.е. –9,16 > –12,38 (шаг неудачный).

1.7. Находим x4 x1 h FS 5 0,8 0,2 1,0;

R(1)= – 11,67; R(1) > R(0,8), т.е. – 11,67 > –12,38 (шаг неудачный)

1.8.Находим x5 x1 h FS 6 0,8 0,1 1 0,7;

R(0,7)= – 11,73; R(0,7) > R(0,8), т.е. – 11,73 > –12,38 (шаг

На основе анализа имеем минимальное значение функции R(1,0)

25

= =– 11,67. Тогда рассматриваемый диапазон сужается до [0,5…1,5], т.е. берутся два прилегающих подынтервала к точке x2 , имеющей минимум целевой функции. Далее осуществляем второй шаг: в связи

сэтим делим прилегающие подынтервалы пополам.

II шаг.

Поскольку на третьем шаге подынтервал разбиения еще не достиг заданной точности поиска, т.е. 0,125 > 0,1 (см. табл. 2), то осуществляем следующий шаг, выбирая в качестве наилучшей точки точку x3, при которой R(x3)=R(0,875) = 12,48. Тогда рассматриваемый интервал сузится до величины [0,75 – 1,0], а [0,5 – 0,75) отбрасываем.

1V шаг.

Поскольку на четвертом шаге подынтервал разбиения оказался меньше заданной точности поиска (см. табл. 2), т.е. 0,0625 < 0,1, то расчеты заканчиваются. В качестве решения задачи принимаем наименьшую величину целевой функции на последнем шаге поиска.

Ответ: Rmin R(0,875 0,1) 12,48.

26

3. Метод золотого сечения.

На первом шаге весь диапазон изменения неизвестной от xmin =0 до xmax =2 разбиваем на три подынтервала следующим образом:

a=xmax –xmin =2 – 0=2;

Наименьшая величина отклика в точке x1 = 0,76, а R(0,76) = – 12,19. Окружаем эту точку прилегающими подынтервалами (0 – 0,76) и (0,76 – 1,24), а остальное (1,24 – 2) из рассмотрения исключаем. Тогда рассматриваемый интервал будет от 0 до 1,24, т.е. a = 1,24. В этом случае получаем новые точки разбиения.

x3 xmin z2 a=0 + 0,38 1,24 = 0,471; x4 xmin z a=0 + 0,62 1,24 = 0,76.

Наименьшая величина отклика в точке разбиения x4=0,76, а

R(0,76)=-12,19.

Согласно вышеизложенной методике рассматриваемый интервал сужается до x3–x2. Тогда имеем a = x3–x2= 1,24 – 0,471 = 0,769.

Отсюда

x5 x3 z2 a=0,471 + 0,38 0,769 = 0,471 + 0,292 = 0,76; x6 x3 z a=0,471 + 0,62 0,769 =0,471 + 0,476 = 0,948.

На новом шаге получим

27

Наилучшая точка здесь x5 = 0,76, а R(0,76) = –12,19. Тогда a = =0,948 – 0,471 = 0,477.

Отсюда

x7=0,471 + 0,38 0,477 = 0,471 + 0,181 = 0,65; x8=0,471 + 0,62 0,477 =0,76 .

Имеем новое разбиение:

Наилучшая точка x8 = 0,76, а R(0,76) = –12,19. Тогда a = 0,948 –

– 0,65 = 0,298.

Отсюда

x9 =0,65 + 0,38 0,298 =0,76; x10 =0,65 + 0,62 0,298 =0,835.

Имеем новое разбиение:

Наилучшая точка x10 = 0,835, а R(0,835) = –12,48. Тогда a = 0,948

– – 0,76 = 0,188.

Отсюда

x11=0,76 + 0,38 0,188 =0,835; x12 =0,76 + 0,62 0,188 =0,876;

Имеем новое разбиение:

28