862

Л. А. Усольцев

ПРИКЛАДНАЯ МАТЕМАТИКА

Учебное пособие

Омск●2008

Федеральное агентство по образованию Сибирская государственная автомобильно-дорожная академия

( СибАДИ )

Л.А. Усольцев

ПРИКЛАДНАЯ МАТЕМАТИКА

Учебное пособие

Омск Издательство СибАДИ

2008

1

УДК 519. 853 ББК 22.182.4 У 76

Рецензенты:

д-р техн.наук, проф. В.А Алексашенко (Центральный Научноисследовательский радиотехнический институт);

доц. Т. В. Гаранина (Зав. Кафедрой математики Омского танкового института)

Работа одобрена редакционно-издательским советом академии в качестве учебного пособия по дисциплине “Прикладная математика” для очной формы обучения студентов

Усольцев Л.А.

У 76 Прикладная математика: Учебное пособие. –Омск: Изд-

во СибАДИ, 2008. – 68с.

ISBN 978-5-93204-402-5

Рассмотрены вопросы общей постановки задачи математического программирования, её геометрической интерпретации, состава задач данного класса, а также математическая постановка задачи нелинейного программирования и методы её решения. В частности, в работе уделено внимание безградиентным и градиентным методам поиска экстремума одномерных и многомерных функций. Кроме того, отдельная глава посвящена составу и области применения аналитических методов поиска экстремумов, а более подробно рассмотрены методы, основанные на классическом математическом анализе и метод неопределённых множителей Лагранжа. Изложение материала ведётся на конкретных примерах решения прикладных инженерных задач.

Табл. 7. Ил.16 . Библиогр.: 6 назв.

2

ВВЕДЕНИЕ

В эпоху глобализации мировой экономики и усиления без того жесткой конкурентной борьбы на мировом экономическом пространстве становятся актуальными вопросы резкого повышения экономичности и эффективности планирования и управления в различных сферах хозяйственной деятельности нашей страны. Эти вопросы становятся первостепенными и особенно насущными накануне вступления России во Всемирную торговую организацию (ВТО), которая потребует на основе объективно сложившейся мировой практики конкурентноспособных товаров и услуг, если мы хотим оставаться активным игроком мирового рынка.

Эффективное решение этих неотложных, насущных вопросов тесно связано сегодня с масштабным техническим переоснащением различных отраслей промышленности и с широкой математизацией знаний как подготовительного этапа к повсеместному использованию информационно-компьютерных технологий для целей оптимизации, в первую очередь работы соответствующих систем.

Настоящее учебное пособие посвящено вопросам математического программирования, в частности нелинейному программированию, а также рассматриваются методы, основанные на классическом математическом анализе, и метод неопределённых множителей Лагранжа в рамках аналитических методов поиска экстремумов.

В первой главе уделено внимание математической постановке, геометрической интерпретации и составу задач математического программирования, дана краткая характеристика линейного и нелинейного программирования и выпуклости функций и множеств. В частности, при рассмотрении задач линейного программирования изложены аспекты целочисленного и частично-целочисленного линейного программирования, типы инженерных задач этого класса и методы их решения. Кроме того, приведен состав задач нелинейного программирования и методы их решения, в частности безградиентные и градиентные методы, а также кратко изложено динамическое программирование и принцип оптимальности Беллмана.

Во второй главе рассматриваются безградиентные методы решения задач нелинейного программирования для одномерных и многомерных функций, излагаются методы сканирования, локализации экстремума, золотого сечения и метод с использованием чисел Фибоначчи для одномерных функций, а также

3

детерминированные методы и методы случайного поиска, предназначенные для многомерных функций. При этом дана сравнительная точность поиска указанными методами.

Третья глава посвящена градиентным методам, в частности методам градиента, релаксаций и крутого восхождения (спуска). Приведены методики и алгоритмы решения задач нелинейного программирования рассматриваемыми методами, обращено внимание на детализацию и основные отличительные особенности.

В главе четвёртой рассматриваются аналитические методы поиска экстремумов одномерных и многомерных функций. Здесь приведен состав указанных методов и более подробно изложены методы, основанные на классическом математическом анализе, уделено внимание необходимым и достаточным условиям

решение конкретных инженерных проблем, которые в работе предлагаются в качестве типовых расчётов. В конце каждой главы приведен перечень вопросов для самоконтроля знаний студентов при закреплении изучаемого материала и подготовке к аттестации. Весь вспомогательный материал для удобства использования вынесен в приложения.

Автор благодарен своим коллегам по кафедре “Информационные технологии” Сибирской государственной автомобильно-дорожной академии за замечания и подготовку рукописи к изданию.

4

Представим рассматриваемую задачу графически (рис. 1). При построении графиков необходимы следующие пояснения. Рассматриваемая задача представляется на плоскости x1 х2. Градация по осям выбирается из расчета, чтобы при построении всех графиков независимые переменные не вышли за пределы выбранных величин. Анализируя соотношения (3)–(7), можно утверждать, что величины х1 и х2 не будут более 1,5.

Приняв, исходя из этого, градуировку по осям х1 и х2 от 0 до 1,5, строим графики: из соотношения (4) имеем х1<0,8. Чтобы определить, в какой полуплоскости от прямой линии х1=0,8 лежит область допустимых решений, выбираем произвольно точку по одну сторону линии х1=0,8. Если эта точка удовлетворяет требованию соотношения (4), то область, в которой лежит выбранная точка, относится к области допустимых решений, в противном случае область допустимых решений расположена на противоположной полуплоскости. Это общее правило определения области допустимых решений. Берем точку х1=0, подставляем ее значение в соотношение

(4) и получаем 0<0,8.

Поскольку соотношение (4) выполняется, а точка х1=0 лежит слева от прямой х1=0,8, то и область допустимых решений лежит слева от этой прямой, т.е. на левой полуплоскости.

Аналогичным образом строим прямую х2=0,8 (5) и определяем изложенным способом, что область допустимых решений лежит ниже прямой х2=0,8. Соотношение (6) – это окружность с единичным радиусом и с центром в начале координат. Причем область допустимых решений может лежать только на окружности, которая построена по соотношению (6).

Особо следует остановиться на целевой функции (3). Кривая, которой может быть представлено соотношение (3), – это гипербола Fi, а вернее, семейство гипербол F1, F2 и т.д. в зависимости от оптимальных значений х1 и х2, симметричных относительно биссектрисы прямого угла с вершиной в начале координат. Иначе говоря, это совокупность гипербол, нанизанных, как на шампур, в виде биссектрисы прямого угла I квадранта декартовой системы координат.

Ограничения (7) (х1=0; х2=0) проходят по осям координат. Все изложенные обозначения и основные точки нанесены на график

6

(см. рис. 1).

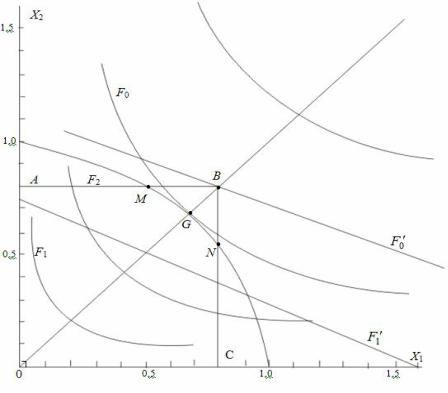
Рис. 1. Геометрическая интерпретация задачи математического программирования

1.2.Состав задач математического программирования

Взависимости от вида целевых функций (3), (3а) и ограничений

(4)– (7) в математическом программировании различают следующие задачи.

I.Задача линейного программирования возникает тогда, когда целевая функция и ограничения – линейные соотношения в виде равенств либо неравенств. Для того чтобы на рассматриваемом примере продемонстрировать задачу линейного программирования, предположим, что целевая функция имеет вид (3а).

Построим прямую линию, соответствующую целевой функции (3а). Для этого (3а) приравняем к цифре 3, иначе 2x1 4x2 3. Эта

величина здесь выбрана исходя из того, что при построении рассматриваемой прямой мы не должны выйти за пределы градаций по осям координат. Построение осуществляем по двум точкам,

7

которые затем соединяем прямой линией.

Если x1=0, то x2=0,75 , а при x2=0 x1=1,5.

Точки (x1=1,5; x2=0) и (x1=0; x2=0,75) наносим на график и соединяем прямой линией F1', как показано на рис.1. Совокупность целевой функции (3а) и соотношений (4), (5) и (7) составляют типичную задачу линейного программирования. Причем, как это видно на рис.1, область допустимых решений ограничена в этом случае квадратом АВСО.

При поиске максимума на графике для определения решения рассматриваемой задачи линию F1', соответствующую целевой функции (3а), необходимо максимально удалить от начала координат, не меняя ее углов наклона в пространстве (прямая F0' ). Если следовать этому правилу, то решением задач (3а), (4), (5) и (7) будет точка В, координаты которой х1=х2=0,8, величина целевой функции,

согласно (3а), будет R(х)=2 0,8+4 0,8=4,8.

II.Задача нелинейного программирования возникает в том случае, когда целевая функция, либо одно или несколько ограничений, либо все одновременно представляют собой нелинейные соотношения.

Если в рассматриваемом примере целевая функция будет задана в виде соотношения (3), а ограничения выражены соотношениями (4) – (7), то это будет типичная задача нелинейного программирования. Графическое решение этой задачи будет располагаться в точке G . Эта точка образована пересечением окружности (6) на ее участке MN, который лежит в области допустимых решений АВСО с целевой функцией (3), соответствующей гиперболе F'0 (см. рис. 1). Иначе говоря, на гиперболе, максимально удаленной от начала координат и имеющей одну-единственную общую точку с областью допустимых решений (точка G). В рассматриваемой задаче область допустимых решений лежит на дуге MN окружности (6), ограниченной квадратом АВСО. Математически координаты точки G можно определить из соотношения (6): х12+х22=1, тогда х12=х22=1, отсюда 2х12 =1, х12 =0,5 и,

наконец, х10 =х02=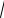0,5=0,7.

Оптимальное значение целевой функции (3) имеем

R(x)=x10 x02 =0,7 0,7=0,49 0,5.

8

1.3. Выпуклые и невыпуклые множества и выпуклые функции

В математическом программировании значительное место уделяется понятию выпуклости функции. Функция называется выпуклой, если она располагается по одну сторону от линии, соединяющей две произвольно выбранные на ней точки.

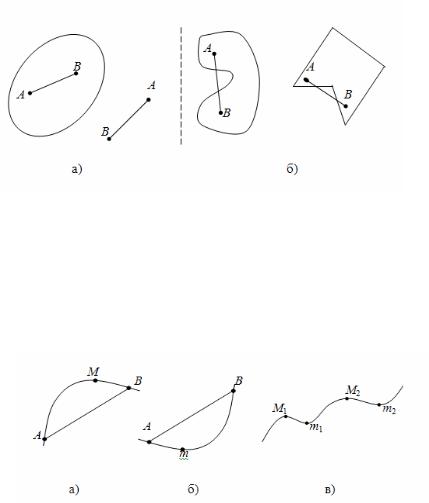
Важным понятием математического программирования является понятие выпуклости множества. Множество называется выпуклым, если две произвольно взятые на нем точки, соединенные между собой прямой линией, принадлежат рассматриваемому множеству. На рис. 2 в качестве примеров приведены выпуклые (а) и невыпуклые (б) множества.

Рис. 2. Примеры выпуклых (а) и невыпуклых (б) множеств

На рис. 3,а изображен пример функции, выпуклой вверх, поскольку ее график расположен выше линии, соединяющей две ее произвольно выбранные точки. На рис. 3, б изображена функция, выпуклая вниз, определение которой аналогично функции, выпуклой вверх, но отличается тем, что функция располагается ниже линии, соединяющей две ее произвольно выбранные точки.

Рис. 3. Выпуклые и невыпуклые функции

9