3.Теоретическая (расчетная) часть

Пусть необходимо смоделировать линейно возрастающий график функции плотности распределения f(x)=mxс заданным математическим ожиданием М(х)=p_s. Подp_sбудем понимать среднее время между событиями вs-ом потоке. Значениеmи значение правой границыа функции распределения пока неизвестны. В основе расчета лежит свойство нормировки функции плотности распределения.

f(x)

x

f(x)=mx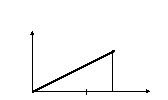

0 M(x)=p_s

1)Рассчитаем угловой коэффициент mчерезаиз условия, что случайная величина х находится в некотором диапазоне (0,а). Вероятность этого события можно выразить через интегральную функцию распределения вероятностейF(x), которая при х =апримет значение 1 (условие нормировки любой функции плотности распределения).

Откуда m=2/a²и можно заданную функцию плотности распределения выразить череза:f(x)=2x/a².

2)Теперь можно рассчитать величину а по заданному значению М(х)=p_s, используя известную формулу для математического ожидания функции случайной величины х:

Откуда находим значения искомых параметров m и а через заданное ps:

3)Определим величину дисперсии:

Таким образом, все неизвестные параметры распределения выражены через p_s.

Интересно сравнить полученную расчетную величину D(x) с дисперсией широко применяемого в СМО экспоненциального закона распределения плотности вероятностей, определяемого формулой:

Для этого закона М(х)=1/, а дисперсияD(x)=1/². Здесь подподразумевается плотность потока событий, связанная со средним интервалом времени между событиям обратной зависимостью 1/=p_s. ОтсюдаD(x) = 1/²=p²_s. Таким образом, дисперсия для линейного закона на конечном диапазоне распределения уменьшается в 8 раз по сравнению с асимптотическим экспоненциальным при одинаковом М(х), что должно приводить к уменьшению очереди и времени ожидания.

4)Определим интегральную функцию распределения F(x) по формуле, аналогичной использованной в п.1, но с переменным верхним пределом, что нужно для выполнения п5:

5)Найдем общуюформулу для расчета теоретических частот_i^т, т.е. ожидаемого числа попаданий моделируемой случайной величины в заданныйi-й интервал внутри диапазона (0,а). Разобьем весь диапазон наkинтерваловравной длины. Координаты границ обозначим кака_i. Тогдаа₀= 0,а₁=а/k,а₂= 2а/k, ……а_k-1= (k-1)a/k,а_k=a. Напомним, что значениеа в данном примере равно 3p_s/ 2. Известно, что теоретическое число попаданий СВ в заданный интервал равно произведению числа разыгранных значенийnна вероятность попадания СВ вi-й интервал, определяемую через разность значений интегральной функции распределения (см. выше формулу в п.4), в которую вместоxследует подставить координаты границi-го интервала:

_i^т=n[F(a_i) -F(a_i-1)] =

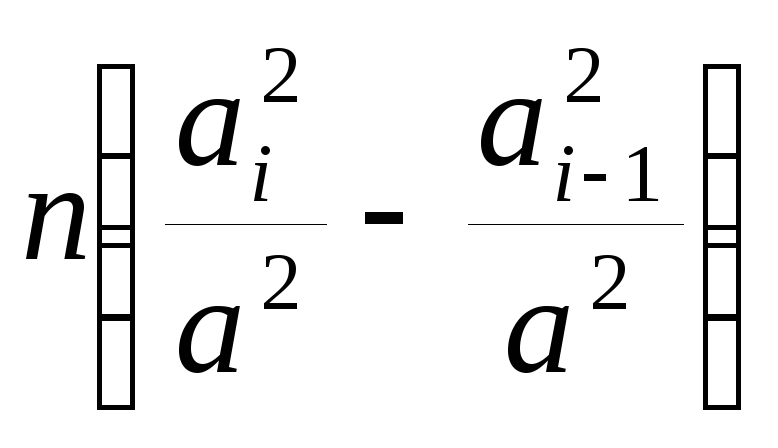
Пусть i= 1, тогда, посколькуa_i-1 =a₀= 0,а₁ =а/k:

Чтобы найти общую формулу зависимости _i^тотi, продолжим вычисления дляi=2:

Аналогично для i=3:

Очевидно, что в качестве коэффициента в обобщенной формуле следует взять нечетное число (2i– 1). Окончательно получим искомую формулу для использования в программе:

Отметим, что значения nиkсвязаны между собой условием устойчивости экспериментальных частот. Согласно этому условию минимальное ожидаемое число попаданий в любой интервал не должно быть меньше 5. В нашем случае это означает, что, так как критичным является 1-й интервал. Для выполнения этого условия из предыдущей формулы находим, что приk=10 число реализаций СВn>=500. С ростомkтребуемое число реализацийnслучайной величины растет пропорциональноk². Например, дляk=15n>=1125.

Приведенные выше расчеты параметров распределения не зависят от метода реализации генератора, но, естественно, относятся только к рассмотренному типу графика функции плотности распределения.Далее рассмотрим два метода реализации данной функции распределения на ЭВМ, используемые в различных вариантах выполнения лабораторной работы.