- •Правительство Российской Федерации
- •Содержание.
- •1.Специальная часть
- •1.1. Описание предметной области по характеристикам замкнутых сау
- •1.1.1. Частотные и логарифмические характеристики сау
- •1.1.2. Частотные показатели (оценки) качества сау
- •1.1.3. Оценка устойчивости сау по ее частотным и логарифмическим частотным характеристикам
- •1.2. Обоснование выбора программных и технических средств для реализации Интернет – подсистемы
- •1.3. Разработка обучающей подсистемы для лабораторного исследования характеристик замкнутых сау в среде интернет.
- •1.4. Разработка структуры меню обучающей подсистемы для лабораторного исследования характеристик замкнутых сау в среде интернет.
- •3.1. Полный допуск
- •3.2. Экспресс-допуск
- •1.5. Разработка методики обучения в Интернет – подсистеме по исследованию устойчивости сау
- •1.6. Разработка методики допуска к лабораторному исследованию устойчивости замкнутой сау с помощью частотных критериев устойчивости
- •1.7. Разработка методики лабораторного исследования устойчивости замкнутой сау
- •1.8. Разработка алгоритмического обеспечения Интернет – подсистемы для лабораторного исследования устойчивости сау
- •1.9. Разработка программного обеспечения обучающей подсистемы для лабораторного исследования характеристик замкнутых сау в среде интернет
- •1.10. Руководство разработчика обучающей подсистемы для лабораторного исследования характеристик замкнутых сау в среде интернет
- •1.11. Руководство пользователя обучающей подсистемы для лабораторного исследования характеристик замкнутых сау в среде интернет
- •1.11.2. Работа в режиме обучения
- •1.11.3. Работа в режиме допуска к лабораторному исследованию
- •1.11.4. Работа в режиме лабораторного исследования
- •2.Конструктивно – технологическая часть
- •2.1. Технический процесс изготовления приборов (имс) по кмдп технологии
- •2.2. Технологический процесс изготовления эпитаксиально – планарного транзистора Типы структур имс
- •Эпитаксия
- •3.Охрана труда
- •4. Экономическая часть
- •4.1. Технико-экономическое обоснование выбора темы.
- •4.2 Сметная стоимость темы
- •4.3 Оценка экономической эффективности проекта.
- •Заключение
- •Список литературы
1.Специальная часть
СПЕЦИАЛЬНАЯ ЧАСТЬ
В специальной части приводится исчерпывающая информация по проектированию и разработке обучающей подсистемы для лабораторного исследования характеристик замкнутых САУ в среде интернет. Приводятся так же сведения о структуре данных системы, алгоритмы программ, структура подсистемы и проводится обоснование выбора программных и технических средств:
описание предметной области;
обоснование выбора программных и инструментальных средств для реализации Интернет – подсистемы;
описание структуры обучающей подсистемы для лабораторного исследования характеристик замкнутых САУ в среде интернет;
описание структуры меню обучающей подсистемы для лабораторного исследования характеристик замкнутых САУ в среде интернет;
методика проведения обучения по исследования устойчивости замкнутой САУ с помощью частотных критериев устойчивости;
методика допуска к лабораторному исследованию;
методика лабораторного исследования обучающей подсистемы для лабораторного исследования характеристик замкнутых САУ в среде интернет;
алгоритмическое обеспечение Интернет – подсистемы по частотным характеристикам и критериям устойчивости САУ;
программное обеспечение Интернет – подсистемы по частотным характеристикам и критериям устойчивости САУ;
инструкции пользователя и разработчика Обучающей подсистемы для лабораторного исследования характеристик замкнутых САУ в среде интернет.
1.1. Описание предметной области по характеристикам замкнутых сау
Совокупность объекта управления и средств автоматического управления называется системой автоматического управления (САУ). Основной задачей автоматического управления является поддержание определенного закона изменения одной или нескольких физических величин в объекте управления.
Основные задачи теории автоматического управления:
• анализ устойчивости, свойств, динамических показателей качества и точности САУ;
• синтез алгоритмов (аналитических выражений), описывающих САУ и обеспечивающих оптимальное качество управления;
• моделирование САУ с использованием компьютеров и универсальных либо специализированных (предметно-ориентированных) прикладных программ;
• проектирование САУ с использованием аппаратных средств вычислительной техники и их программного обеспечения (средств автоматизации программирования и проч.).
1.1.1. Частотные и логарифмические характеристики сау
Частотными характеристиками обыкновенной линейной САУ (рис.1.1) называется Формулы и графики, характеризующие реакцию системы на гармоническое входное воздействие в установившемся режиме.
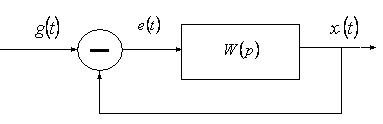
Рис. 1.1
Гармоническое
входное воздействие
- это функция времени, которая может
быть представлена в виде линейных
комбинаций функций
![]() и
и
![]() .
Если на вход системы подать гармоническое
воздействие
.
Если на вход системы подать гармоническое
воздействие
|
|
(1) |
где
![]() –
амплитуда воздействия;
–
амплитуда воздействия;
![]() - угловая частота воздействия, то на
выходе системы в установившемся режиме
будет также гармоническая функция той
же частоты
- угловая частота воздействия, то на
выходе системы в установившемся режиме
будет также гармоническая функция той
же частоты
![]() ,
но в общем случае сдвинутая по фазе
относительно входной величины на угол
,
но в общем случае сдвинутая по фазе
относительно входной величины на угол
![]() ,
т.е.
,
т.е.
|
|
(2) |
где
![]() -
амплитуда выходной величины;
-
амплитуда выходной величины;
![]() - сдвиг фаз между выходной и входной
величинами.
- сдвиг фаз между выходной и входной
величинами.
Передаточные функции и уравнения замкнутой системы
Из цепи звеньев любой сложности, показанной на рисунке получается замкнутая система при помощи единичной отрицательной обратной связи. Эту братную связь называют главной в отличии от местных обратных связей, которые могут быть внутри в составе разомкнутой цепи звеньев.

Пусть имеются внешние воздействия: g(t) – задающее и f(t) – возмущающее. В общем случае могут быть введены несколько возмущающих воздействий, приложенных в разных местах системы.
Задана передаточная функция разомкнутой цепи:
![]()
В виде отношения многочленов с единичными коэффициентами при младших членах, т.е.
![]()
где K – общий коэффициент усиления разомкнутой системы.
Передаточные функции замкнутой системы записываются отдельно для каждой комбинации входа и выхода, а значит, и для каждого внешнего воздействия в отдельности.
Разделим каналы прохождения сигналов в сиситеме от каждого внешнего воздействия. Возмущающее воздействие f(t) может быть приложено в любом месте. Но, используя второе правило структурных преобразований всегда можно выделить ту часть схемы, через которую проходят сигналы от f(t) на выход x. Это показано на рисунке в виде передаточной функции M(s):
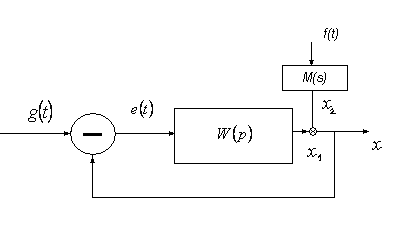
Для задающего воздействия g(t) схема прохождения сигналов сохраняется в полном виде W(s). На выходе имеем формально:
![]()
(на самом деле M(s) входит в общую схему как часть W(s))
Основные соотношения, следовательно, в изображениях по Лапласу будут иметь вид:
E=G-X (1)
X=W(s)E+M(s)F. (2)
В расчетах автоматических систем применяют три основных вида передаточных функций замкнутой системы.
1.Главная передаточная функция замкнутой системы ( при f(t)=0);
Ф(s)
= ![]()
из формулы (1) и (2) при F=0 имеем:
X=W(s)(G - X),
откуда
![]()
2. Передаточная функция замкнутой системы для ошибки (при f(t) = 0);
![]()
По формуле (1) получаем:
![]()
откуда
![]()
3. Передаточная функция замкнутой системы по возмущающему воздействию (при g(t) = 0);
![]()
Из формул (1) и (2) при G = 0 имеем:
X = W(s) ( -X) + M(s)F
откуда
![]()
Где R(s)
= L(s)M(s),
причем многочлен R(s) зависит от места
приложения возмущающего воздействия.
Заметим, что поскольку при g(t) = 0 имеем
E = - X, то передаточная функция замкнутой
системы для ошибки по возмущающему
воздействию ![]() будет той же,
что и для регулируемой величины
будет той же,
что и для регулируемой величины ![]() с точностью до знака.
с точностью до знака.
Важно отметить, что знаменатель всех видов передаточной функции замнутой системы один и тот же.
Для наглядного представления частотных свойств САУ используются следующие частотные характеристики:
1)
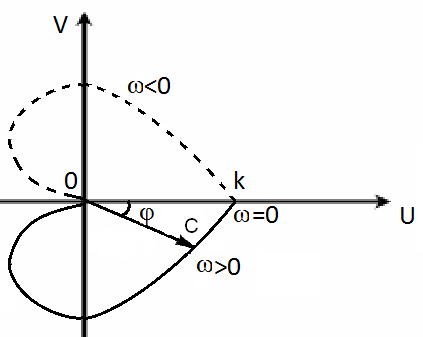
Амплитудно-фазовая
частотная характеристика (АФЧX)
![]() -это кривая, описываемая концом вектора
-это кривая, описываемая концом вектора
![]() на комплексной плоскости U-V
(годограф вектора
на комплексной плоскости U-V
(годограф вектора
![]() )
при изменении частоты входного воздействия
)
при изменении частоты входного воздействия
![]() от -
до +
(рис.1.2). Длина вектора, проведенного из
начала координат в точку АФЧК,
соответствующую какой-либо выбранной
частоте
от -
до +
(рис.1.2). Длина вектора, проведенного из
начала координат в точку АФЧК,
соответствующую какой-либо выбранной
частоте
![]() ,
равна модулю
,
равна модулю
![]() ЧПФ.
ЧПФ.
Угол между
этим вектором и положительным направлением
вещественной оси равен аргументу
или фазе
![]() ЧПФ. АФЧХ соответствует выражение (5).
ЧПФ. АФЧХ соответствует выражение (5).
|
|
|
|
|
Рис. 1.2. |
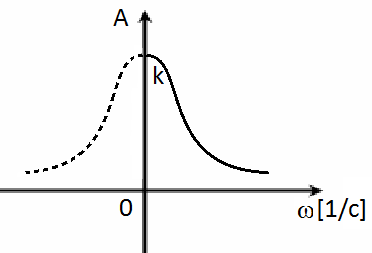
Рис.1.3 |
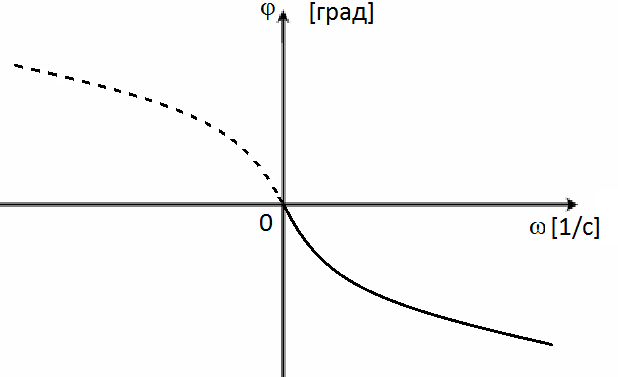
Рис. 1.4 |
амплитудная частотная характеристика (ЯЧХ)
 - это
кривая
изменения отношения амплитуд
выходной и входной величин в зависимости
от частоты
- это
кривая
изменения отношения амплитуд
выходной и входной величин в зависимости
от частоты
 (рис.1.3). Она показывает, как пропускает
САУ сигнал различной частоты. АЧХ
соответствует выражение (8).
(рис.1.3). Она показывает, как пропускает
САУ сигнал различной частоты. АЧХ
соответствует выражение (8).Фазовая частотная характеристика (ФЧХ)
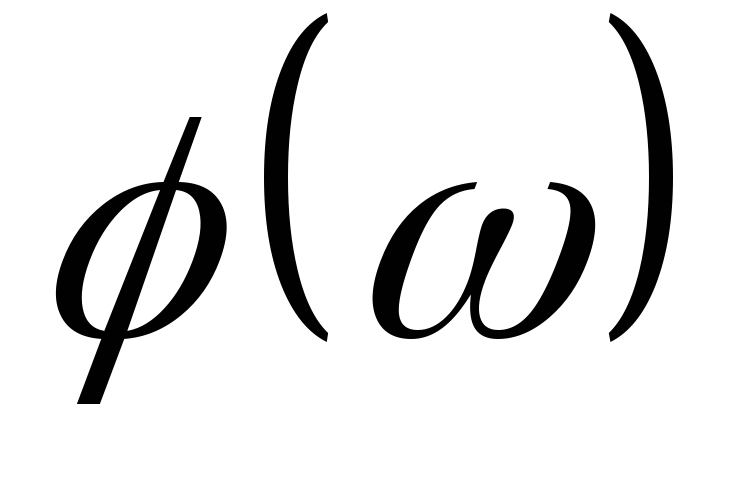 - это кривая изменения сдвига фаз
выходной величины по отношению к входной
в зависимости от частоты
- это кривая изменения сдвига фаз
выходной величины по отношению к входной
в зависимости от частоты
 (рис.1.4). Она показывает фазовые сдвиги,
вносимые САУ на различных частотах.
ФЧХ соответствует выражение (9).
(рис.1.4). Она показывает фазовые сдвиги,
вносимые САУ на различных частотах.
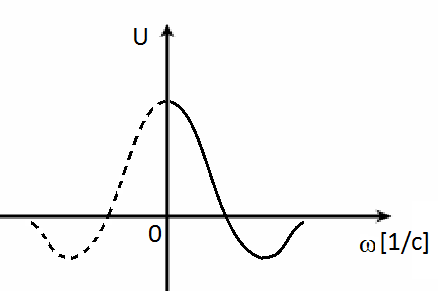
ФЧХ соответствует выражение (9).Вещественная частотная характеристика (ВЧК)
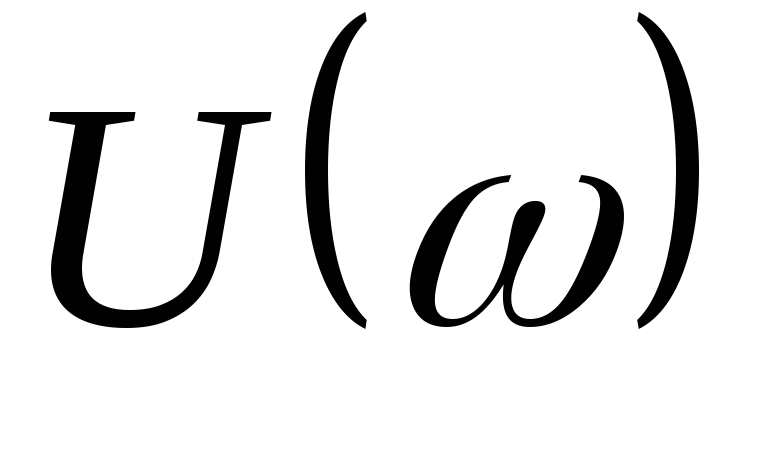 - это кривая, которой соответствует
вещественная составляющая ЧПФ (рис.1.5)
и выражение (6).
- это кривая, которой соответствует
вещественная составляющая ЧПФ (рис.1.5)
и выражение (6).Мнимая частотная характеристика (МЧХ)
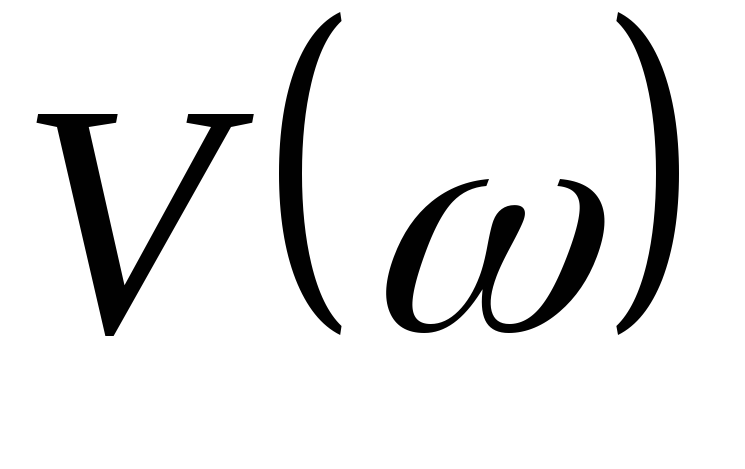 - это кривая, которой
соответствует
мнимая составляющая ЧПФ (рис.1.6) и
выражение (7).
- это кривая, которой
соответствует
мнимая составляющая ЧПФ (рис.1.6) и
выражение (7).
|
|
|
|
Рис.1.5. Вещественная частотная характеристика – ВЧХ |
Рис.1.6. Мнимая частотная характеристика – МЧХ |
Кривые АФЧХ, ФЧХ, ВЧХ,
МЧХ обладают свойством симметрии.
Поэтому по результатам вычисления
кривых для положительных частот можно
построить кривые для всего диапазона
частот
![]() ,
так как
,
так как
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
В связи с этим исследование звеньев
(систем) можно проводить только в
положительном диапазоне частот, тем
более, что отрицательные частоты реально
не существуют.
.
В связи с этим исследование звеньев
(систем) можно проводить только в
положительном диапазоне частот, тем
более, что отрицательные частоты реально
не существуют.
Исследование САУ значительно упрощается при использовании логарифмических частотных характеристик.
Логарифмическая
амплитудная частотная характеристика
(ЛАЧХ)
![]() – это кривая
(рис.1.7), построенная в логарифмическом
масштабе
частот
в соответствии с выражением:
– это кривая
(рис.1.7), построенная в логарифмическом
масштабе
частот
в соответствии с выражением:
|
|
(10) |
Единицей измерения
величины
![]() ,
которая
откладывается по оси ординат, является
децибел. По оси абсцисс откладывается
частота
,
которая
откладывается по оси ординат, является
децибел. По оси абсцисс откладывается
частота
![]() в логарифмическом масштабе
в логарифмическом масштабе
![]() .
Равномерной единицей по оси абсцисс
является декада – это любой отрезок,
на котором значение частоты увеличивается
в 10 раз.
.
Равномерной единицей по оси абсцисс
является декада – это любой отрезок,
на котором значение частоты увеличивается
в 10 раз.
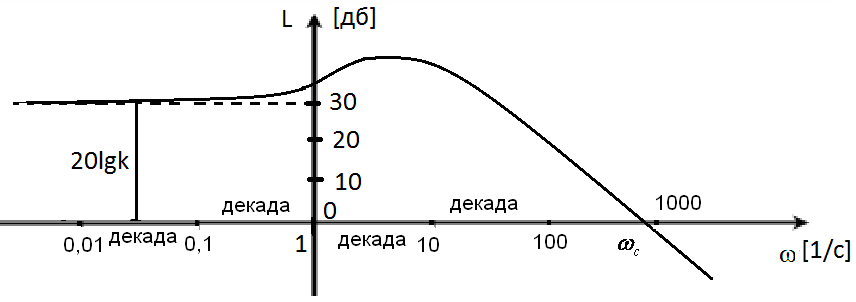
Рис.1.7. Логарифмическая амплитудная частотная характеристика.
Точка пересечения ЛАЧХ
с осью абсцисс называется частотой
среза
![]() .
Она определяется из условия
.
Она определяется из условия
|
|
(11) |
Ось абсцисс
(![]() )
соответствует значению
)
соответствует значению
![]() =l,
т.е. прохождению амплитуды сигнала через
САУ без изменения. Верхняя полуплоскость
ЛАЧХ соответствует значениям
=l,
т.е. прохождению амплитуды сигнала через
САУ без изменения. Верхняя полуплоскость
ЛАЧХ соответствует значениям
![]() ,
т.е. усилению амплитуды, а нижняя
полуплоскость – значениям
,
т.е. усилению амплитуды, а нижняя
полуплоскость – значениям
![]() ,
т.е. ослаблению амплитуды. ЛАЧХ может
быть приближенно построена в виде
асимптотической
ЛАЧХ,
представляющей собой совокупность
отрезков прямых линий (асимптот) с
наклонами, кратными величине 20 дб/дек.
,
т.е. ослаблению амплитуды. ЛАЧХ может
быть приближенно построена в виде
асимптотической
ЛАЧХ,
представляющей собой совокупность
отрезков прямых линий (асимптот) с
наклонами, кратными величине 20 дб/дек.
Логарифмическая
фазовая частотная характеристика (ЛФЧХ)
- это кривая ФЧХ
![]() ,
построенная в логарифмическом масштабе
частот (рис.8). Как и при построении ЛАЧХ
по оси абсцисс откладывают значение
частоты
,
построенная в логарифмическом масштабе
частот (рис.8). Как и при построении ЛАЧХ
по оси абсцисс откладывают значение
частоты
![]() в логарифмическом масштабе
в логарифмическом масштабе
![]() ,
а записывают действительное значение
частоты. По оси ординат откладывают
значении функции
,
а записывают действительное значение
частоты. По оси ординат откладывают
значении функции
![]() .
Таким образом, ЛФЧХ – это зависимость
.
Таким образом, ЛФЧХ – это зависимость
![]() от логарифма частоты
от логарифма частоты![]() .
.
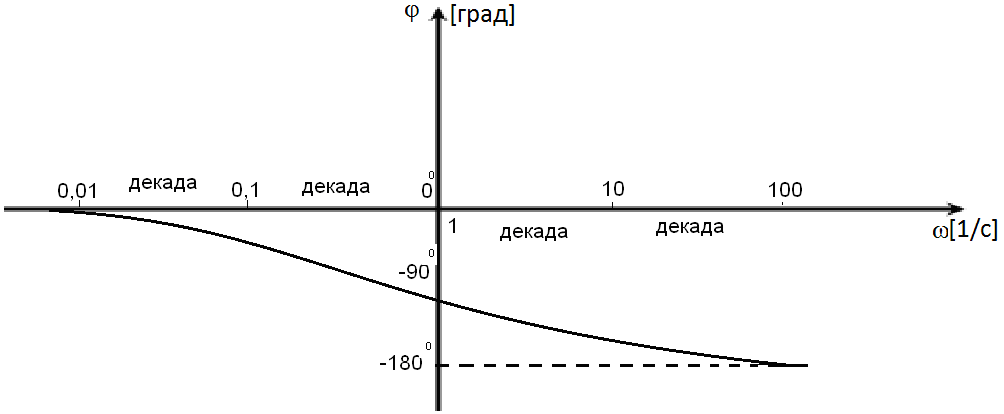
Рис.1.8. Логарифмическая фазовая частотная характеристика.