11.4. Анимация

П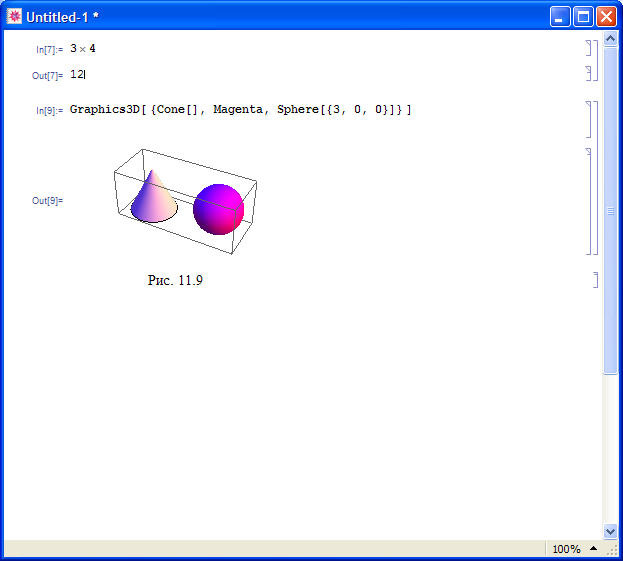акет Математика позволяет “оживлять” построенные графики; для этого нужно выделить их и выбрать команду менюGraphics – Rendering – Animate Selected Graphics (Ctrl+Y). Графики будут поочередно сменять друг друга на экране монитора. При анимации может оказаться полезной команда выравнивания графиков: Graphics – Rendering – Align Selected Graphics.

Другой способ построения анимированных объектов – использование функции Animate.

Функция Animate[expr, {u, umin, umax}] создает анимацию выражения expr, в котором параметр u меняется от umin до umax. Может быть указан шаг изменения параметра: {u, umin, umax, du}. При этом выражение expr может быть любым, не обязательно рисунком.

Пример 11.8. Команда

In[ ]:= Animate[{n, Prime[n]}, {n, 1, 50, 1}]

выводит на экран поочередно простые числа вместе с порядковым номером числа.

Пример 11.9. Написанная ниже программа выводит на экран анимированный график – катящееся колесо. Точка обода колеса вычерчивает циклоиду. Один из кадров графика показан на рис. 11.10.

In[ ]:= tp=0.2; Animate[ ParametricPlot[

{ {Cos[Pi/2-t*4Pi]+4Pi*tp, Sin[Pi/2-t*4Pi]+1}, (*Колесо *)

{Cos[Pi/2-t*4Pi*tp]+4Pi*t*tp, Sin[Pi/2-t*4Pi*tp]+1}, (*Циклоида*)

{4Pi*tp+Cos[Pi/2-4Pi*tp]*t, 1+Sin[Pi/2-4Pi*tp]*t}, (*Радиус*)

{-1+t*(4Pi+2), 0} , (*Рельс*)

{0, t*2.5} (*Начало координат*)

}, {t, 0, 1},

AspectRatio -> Automatic, PlotRange -> All ],

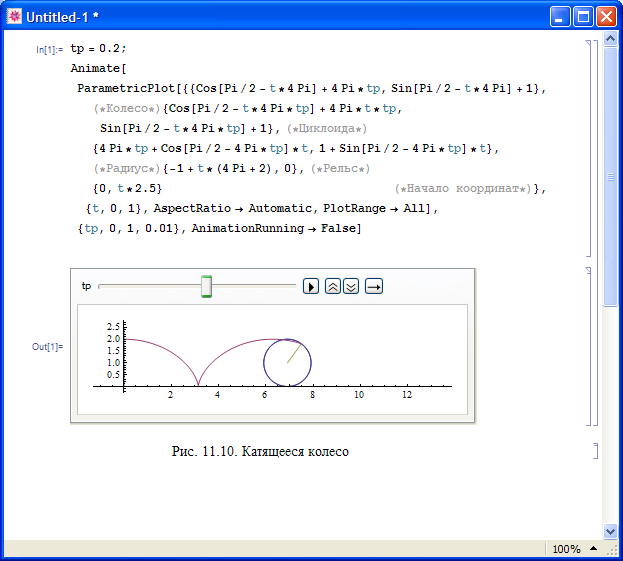{tp, 0, 1, 0.01}, AnimationRunning -> False]

Опция AnimationRunning -> False означает, что анимация выводится на экран в состоянии паузы.

12. Функция Manipulate

Ф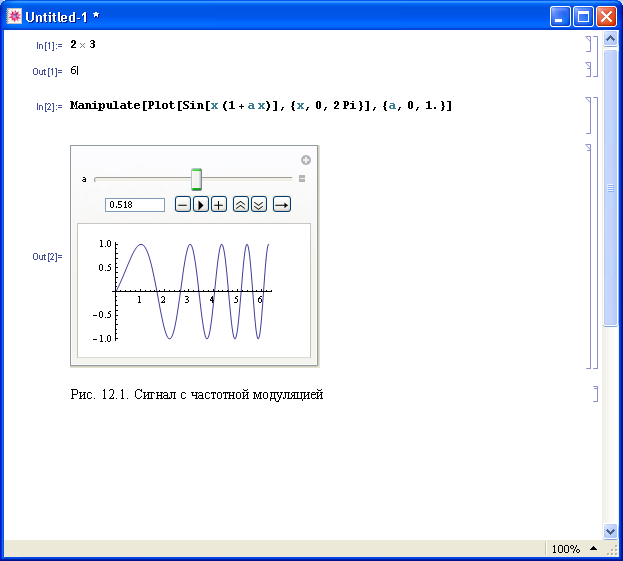ункцияManipulate[expr, {u, u_min, u_max}] позволяет ввести в выражение expr элемент управления, дающий возможность изменять это выражение в диалоговом режиме. Выражение может быть произвольным. Оно может включать вычислительные или аналитические операции, может также описывать графики.

Пример 12.1. Построим график колебаний с линейной частотной модуляцией, с возможностью изменения коэффициента модуляции. Для этого напишем команду:

In[ ]:= Manipulate[Plot[Sin[x (1 + a x)], {x, 0, 2Pi}],

{a, 0, 1.}]

Выполнив команду, увидим график синусоиды и над ним полосу прокрутки с движком в начальном левом положении. С помощью полосы прокрутки можно изменять значение параметраа. Щелкнув на знаке “+” в конце полосы прокрутки, откроем дополнительные диалоговые элементы: окно с текущим значением параметра а и кнопки управления. Окончательный вид графика показан на рис. 12.1. Щелкнув мышкой на черном треугольнике, включим анимацию: значение папраметра будет автоматически меняться от 0 до1.

Команда Manipulate[expr, {u, u_min, u_max, du}] вводит в выражение expr элемент управления, который можно изменять в пределах от u_min до u_max с шагом du.

Пример 12.2. Напишем команду, позволяющую вывести на экран формулы бинома Ньютона степени от 0 до 10:

In[ ] := Manipulate[Expand[(x+y)^n], {n, 0, 10, 1}]

Результат работы команды показан на рис. 12.2. В окне видим степень бинома. Кнопки “+” и “–” позволяют увеличивать и уменьшать степень. Щелкнув на черном треугольнике, запустим анимацию – автоматическое изменение степени. Остальные три кнопки позволяют менять скорость и направление автоматического изменения степени.

КомандаManipulate[expr, {u, {u₁, u₂, …}}] вводит элемент управления, который принимает заданные значения u₁, u₂, ….

Команда Manipulate[expr, {u, …}, {v, …}, …] вводит несколько элементов управления.

Пример 12.3. Напишем команду для построения фигур Лиссажу:

In[ ] := Manipulate[ParametricPlot[{Cos[m x], Sin[n x]},

{x, 0, 2Pi}], {m,{1, 3, 5}}, {n, {1, 2, 3, 4, 5}}]

Результат выполнения команды показан на рис.12.3. Выбрать нужное значение параметра можно, щелкнув на соответствующей кнопке. Можно также включить автоматический просмотр всех фигур, щелкнув на знаке “+” и запустив команду autorun.