ВЫСШАЯ МАТЕМАТИКА_ГОРНЫЙ

Добавил:

spbguap9 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

Добыча нефти и газа

Файл:

0) также непрерывны в точке

.pdf

Скачиваний:

Добавлен:

03.01.2021

Размер:

1.01 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

СПБГУАП группа 4736 Контакты https://new.guap.ru/i03/contacts

x x .			(4.15).
	α x β x
Относительная погрешность равенства (4.15)		в силу теоремы 2
	α x

стремится к нулю.
4.21. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Пусть функция f (x) определена в окрестности точки			x x0 , так что в

точке x0 функция имеет определенное значение f (x0 ).

Определение 1. Функция f (x) называется непрерывной в точке х = х0

(при x x0 ), если предел функции и ее значение в точке х = х0 равны, т.е.

			lim f x f x0 .					(4.16)
			x x0
Замечание 1. На «языке последовательностей» непрерывность функции
f (x) в точке x x0	можно сформулировать так: функция						f (x) называется
непрерывной в точке		x x0	(при x x0 ), если для любой сходящейся к x0
последовательности	xn		значений аргумента		x x0 ,		соответствующая
последовательность f xn значений функции сходится к							f x0 .
Замечание 2. На графике функции				f (x) равенство (4.16) означает, что
при стремлении x	к	x0 ,	ордината	f (x) стремится к			ординате	f (x0 ).
Следовательно, условие непрерывности функции						f (x)	в точке	x x0
означает, что ее график «непрерывен»				при всех	x,	достаточно близких к
данной точке.

Замечание 3. Основные элементарные функции непрерывны во всех точках, где они определены, что видно из их графиков в области определения

и свойств.
Замечание 4. Заметим, что		lim x x0 и потому условие непрерывности
	x x0
(4.16) можно записать в виде:		lim	f (x) f ( lim x ) , т.е. для непрерывной
	x x0		x x0
функции знак функции и знак предела можно переставлять.
Например,
	1			1
lim ln(1 x)	x lnlim(1 x) x lne 1,
x 0			x 0

так как функция ln x непрерывна.

Приведем еще одно определение непрерывности функции в точке x0 .

Заметим, что условия x x0 и x x0 0 равносильны, и, следовательно, равенство (4.16) можно переписать в виде

СПБГУАП группа 4736 Контакты https://new.guap.ru/i03/contacts

						lim f x f x0 0.	4.17)
у						x x0 0
						x x0 0

			f (х0)	f (х0)		Определение 2. Разность х – х0 назы-
			f (х0)	f (х0)	вается приращением аргумента		x в точке
					x0	и обозначается x : x x x0 . Отсюда
					x0	и обозначается x : x x x0 . Отсюда
		f (х)			x x0 x .
О	х		х0	х		Определение 3. Разность f x f x0
О	х		х0	х		Определение 3. Разность f x f x0
		х			называется приращением функции в точке
		х			называется приращением функции в точке
					x0 ,	вызванным приращением	аргумента
		Рис.4.4			x , и обозначается y или f x0 :

f x0 f x f x0 f x0 x f x0 .

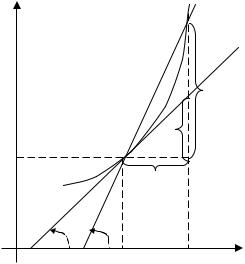
Геометрический смысл приращений очевиден из рис.4.4. Равенство (4.17) в новых обозначениях принимает вид

lim f x0 0 или	lim y 0 .
x 0	x 0

Таким образом, если бесконечно малому приращению аргумента в точке x x0 соответствует бесконечно малое приращение функции, то функция в этой точке непрерывына. Справедливо и обратное утверждение.

Пример 4.11. Показать, что функция y x2

непрерывна

для любого

значения аргумента x.

Решение. Найдем y и его предел при x 0:

y (x x)2 x2 x2 2x x ( x)2 x2 2x x ( x)2;

lim y lim (2x x ( x)2 ) 2x lim x lim ( x)2

x 0

Итак, lim y 0 для любого x.

x 0

Пример 4.12. Показать, что функция

y cosx

непрерывна для любого

аргумента x.

Решение. Найдем y :

sin

y cos(x x) cosx 2sin x

sin

sin x

x .

Известно, что

sin

lim

sin x

x 0

Тогда при любом x

имеем

lim y 0.

x 0

СПБГУАП группа 4736 Контакты https://new.guap.ru/i03/contacts

Определение 4. Функция f (x) называется непрерывной в точке x x0

справа, если выполняется предельное равенство
	f (x0 0)		lim	f (x) f (x0 ).
			x x0 0
Аналогично определяется непрерывность функции f (x)						в точке	x x0
слева:	f (x0 0)		lim	f (x) f (x0 ).
	f (x0 0)		lim	f (x) f (x0 ).
			x x0 0
Определение 5.	Функция	f (x) называется непрерывной на интервале
(a,b), если она непрерывна в каждой точке этого интервала.
Определение 6. Функция		f (x) непрерывна на отрезке a,b , если она
непрерывна на интервале (a,b)			и непрерывна		на концах	отрезка	a,b
соответственно справа и слева.
4.22. РАЗРЫВ ФУНКЦИИ. ТОЧКИ РАЗРЫВА
Пусть функция	f (x) определена			при всех	значениях	x , достаточно
близких к точке x x0 .		f (x)
Определение 1.	Функция	f (x)		при x x0	(в точке	x x0 )	имеет

разрыв, если в этой точке нарушается хотя бы одно из условий непрерывно-

сти. При этом точка x x0

называется точкой разрыва.

Определение 2. Если существуют конечные левосторонние и правосто-

ронние пределы функции при

x x0 , но они не равны друг другу, т.е.

f (x0 0) f (x0 0),

то точка х = х0 называется точкой разрыва первогорода.

Заметим, что если

f (x0 0) f (x0

0) f x0 , то точка х = х0 называется

точкой устранимого разрыва.

Определение 3. Если хотя бы один из односторонних пределов не

существует или равен бесконечности,

то точка

x x0

называется точкой

разрыва второго рода.

Для примера рассмотрим несколько функций.

1. f x arctg

Область

определения функции:

,0 0 .

В точке x 0 она не определена.

Заметим, что

lim f x lim arctg

;

lim f x lim arctg

x 0

Следовательно, функция f x arctg1 в точке х = 0 имеет разрыв первогорода. x

СПБГУАП группа 4736 Контакты https://new.guap.ru/i03/contacts

2. Функция f (x) sin x . В точке х = 0 имеет устранимый разрыв. x

Действительно, значение функции при х = 0 не определено, но существуют конечные и равные друг другу лево- и правосторонние пределы:

lim

sin x

lim

sin x

x 0

Если доопределить функцию, положив

f (0) 1, то функция

sin x

f (x)

при

x 0;

при

x 0

станет непрерывной в точке x 0.

3. Функция

f x

sin x

. Вточке x 0 имеет разрыв первого рода, так как

f ( 0) lim

sin x

f ( 0) lim

sin x

x 0

4. Функция

f (x) cos

. В точке

x 0 имеет разрыв второго рода, так

как оба односторонних предела

lim cos

не существуют.

x 0

5. Функция f x . Ее область определения ,0 0 . x2

В точке x 0 функция не определена. Заметим. что

lim f x lim		1	;
lim f x lim		x2	;
x 0	x 0	x2
x 0	x 0
	x 0

lim f x lim		1	.
lim f x lim		x2	.
x 0	x 0	x2
x 0	x 0
	x 0

Следовательно, функция f x 1 в точке х = 0 имеет разрыв второго рода. x

4.23. ОСНОВНЫЕ СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ

Теорема 1. Если функции f x и g x непрерывны в точке x x0 , то сумма и разность функций f x g x , произведение f x g x и частное

СПБГУАП группа 4736 Контакты https://new.guap.ru/i03/contacts

Доказательство. Непрерывные в точке x x0 функции f x иg x

имеют в этой точке пределы f x0 и g x0 соответственно. По теореме 1 раз-

дела 4.14 функции f x g x , f x g x		и	f x	имеют соответственно
			g x
	f x0
пределы f x0 g x0 , f x0 g x0 и		. Тогда по первому определению
	g x0

непрерывности функции в точке x x0 все перечисленные функции в этой точке непрерывны.

Теорема 2. Если функция u φ x непрерывна в точке x x0 , а функция

y	f u непрерывна в соответствующей точке	u0 φ x0 , то функция
y	f φ x непрерывна в точке x x0 .

Доказательство вытекает из определения непрерывности функций: основные элементарные функции в области их определения непрерывны.

Теорема Вейерштрасса (без доказательства). Если функция f(x) непрерывна на отрезке a,b , то на этом отрезке обязательно найдутся две точки c1 и c2 , где достигаются наибольшее (М) и наименьшее (m) значения

функции f (x) на [а, b]: f (c1) M, f (c2)	m, причем	m f (x) M.
Замечание. Последнее неравенство	показывает,	что если f (x) на

отрезке a,b непрерывна, то она на этом отрезке ограничена. Действительно,

пусть K max

. Тогда

f x

K ( K 0,K const).

Теорема Коши (без доказательства). Если функция f (x) непрерывна на отрезке a,b и на концах отрезка принимает значения разных знаков, то внутри отрезка обязательно найдется по крайней мере одна точка x c такая,

что f (c) 0.

Из геометрических соображений очевидно, что при переходе непрерывной функции из одной полуплоскости в другую, график функции пересечет ось Ox по крайней мере в одной точке.

Следствие. Если функция f (x) непрерывна на отрезке a,b и прини-

мает на этом промежутке наибольшее (М) и наименьшее (m) значения и μ –

такое число, что	m μ M,	то внутри отрезка найдется по крайней мере
одна точка x c	такая, что f	(c) μ.

СПБГУАП группа 4736 Контакты https://new.guap.ru/i03/contacts

Вопросы для самопроверки

1.Сформулируйте определение функции и области ее определения.

2.Что называется числовой последовательностью?

3.Дайте определение бесконечно малой последовательности.

4.Сформулируйте свойства бесконечно малых последовательностей.

5.Дайте определение бесконечно большой последовательности.

6.Сформулируйте свойства бесконечно больших числовых последовательностей.

7.Какая связь существует между бесконечно малыми и бесконечно большими последовательностями?

8.Дайте определение предела последовательности и укажите его геометрический смысл.

9.Какой предел называют первым классическим (замечательным) и какие пределы следуют из него?

10.Какие пределы называют вспомогательными?

11.Сформулируйте определение предела функции на «языке последовательности» и на «языке ε – δ».

12.Какие теоремы теории пределов вам известны?

13.Какие функции называются бесконечно малыми и бесконечно большими?

14.Какими свойствами обладают бесконечно малые и бесконечно большие функции и какова связь между ними.

15.Какой предел называют вторым классическим (замечательным) пре-

делом?

16.Какие бесконечно малые называют эквивалентными и как их исполь-

зуют для раскрытия неопределенности вида 0 ?

17.Какие бесконечно малые называют бесконечно малыми одного порядка?

18.Сформулируйте определениенепрерывности функции в точке х = х0.

19.Какие точки называют точками разрыва функции и какова их классификация?

20.Какие свойства непрерывных функций вам известны?

Тесты

№	Вопрос		Варианты ответа
п/п	Вопрос		Варианты ответа
п/п

1	Какие бесконечно малые при	1.	tg2x ~ x2
	x 0 не являются эквива-	2.	1 cos2x ~ 2x2
	лентными?	2.	1 cos2x ~ 2x2
	лентными?	3.	ln(1 5x)~ 5x
		3.	ln(1 5x)~ 5x
		4.	cos5x cos3x ~ 2x

СПБГУАП группа 4736 Контакты https://new.guap.ru/i03/contacts

		Продолжение таблицы

№	Вопрос	Варианты ответа
п/п	Вопрос	Варианты ответа
п/п

2	lim	(x 5)					2		5		2	равен			1.	10
		(x 5)							5						2.	25
					x										2.	25
	x 0				x										3.	2x2
															3.	2x2
															4.	25x

3	Указать область определения														1.	1/2; 5/3
	функции y log2x 5 3x														2.	0; 1/2)
															3.	0; 1/2) 1/2; 5/3
															4.	5/3 ;

4	Последовательность yn на-														1.	E 0 N :n N		yn			E
4	Последовательность yn на-														1.	E 0 N :n N		yn			E
	зывается							бесконечно боль-							2.	E 0 N :n N	yn			E
	зывается							бесконечно боль-							2.	E 0 N :n N	yn			E
	шой, если														3. E 0 N :n N		yn		E
	шой, если

															4. E 0 N :n N		yn		E
															4. E 0 N :n N		yn		E

5			2			5x									1.	0
	lim			sin		5x					равен				2.	5/2
	lim		2								равен				2.	5/2
	x 0 ln (1 2x)														3.	25/4
															3.	25/4
															4.

6	Какая из указанных функций														1.	y ln(x 2)
	в точке						x 2						не является		2.	y (x 2)2
	бесконечно большой?														3	y ctg(x 2)
															3	y ctg(x 2)
															4.	y tg(x 2) 2

7
7	lim							12x						равен	1.	3
								12x							1.	3

															2.	12/8
	x
	x				4x					8x			3x

															3.	4
															3.	4
															4.	0

8	Какое утверждение в общем														1.	φ(x) ψ(x) – бесконечно малая
	случае неверно, если (х) и														функция
	(х) – бесконечно малые														2.	x / x – бесконечно малая
	функции при x a?														функция
															3.	(x) (x) – бесконечно малая
															функция
															4.	Функции (x) и (x) ограничены

СПБГУАП группа 4736 Контакты https://new.guap.ru/i03/contacts

			Окончание таблицы

№	Вопрос		Варианты ответа
п/п	Вопрос		Варианты ответа
п/п

9 Числовая последовательность		1. Монотонно возрастает (или убывает)
	имеет конечный предел, если	и ограничена
	она	2.	Ограничена
		3.	Монотонна
		4. Строго возрастающая

10 lim(1 tg2	x	)ctg2x равен	1.	1
x 0			2.	1/е
			3.	e1/2
			4.	e2

СПБГУАП группа 4736 Контакты https://new.guap.ru/i03/contacts

Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

5.1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ПРОИЗВОДНОЙ

Задача об определении скорости точки. Пусть материальная точка движется прямолинейно и неравномерно вдоль оси Oх по закону x f (t). Требуется найти ее скорость в момент времени t.

Пусть в момент времени t точка находилась в положении М на расстоянии х от начала координат О (рис.5.1). За время t она, не меняя направления движения, заняла положение М1 с абсциссой x x. Таким образом, за время t путь, пройденный движущейся точкой, изменился на x. Очевидно, что

x f (t t) f (t) , а отношение

определит среднюю скорость точки Vср

М1

за время t. Мгновенная скорость точ-

ки в момент t

Рис.5.1

lim V

lim

f (t t) f (t)

(5.1)

мгн

t 0 ср

t 0 t

t 0

Данная формула определяет скорость точки в прямолинейном переменном движении. Например, при свободном падении тяжелой материальной точки в пустоте закон движения определяется формулой x gt2 / 2 , где g – ускорение свободного падения. Тогда скорость точки в произвольный момент времени вычисляется по формуле (5.1)

g t t 2

gt2

g t

V lim

lim

t 0 t

t 0

5.2.ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ, ЕЕ ГЕОМЕТРИЧЕСКИЙ

ИМЕХАНИЧЕСКИЙ СМЫСЛ

Пусть функция y f (x) задана на некотором промежутке X. Возьмем конечную точку x X и дадим ей произвольное приращение x 0 , такое, что x x X . Приращение функции в точке х, соответствующее приращению аргумента x , y f x x f x .

Определение 1. Конечный или бесконечный предел отношения приращения функции y к вызвавшему его приращению аргумента x при условии, что x 0 ( x 0), называется производной функции у = f(x) по пере-

менной х и обозначается у , f (x) или yx . Итак,

СПБГУАП группа 4736 Контакты https://new.guap.ru/i03/contacts

lim

f x x f x

(5.2)

x lim

x 0 x

x 0

Пример 5.1.

Найти

производную

функции f x x2 в

произвольной

точке x.

Решение. По определению имеем

(x x)2 x2

(x) (x

) lim

x 0

= lim

x2 2x x x 2

lim

x 2x x

2x.

x 0

Таким образом, x

n–1

2x. Можно такжепоказать, что (х )

= nx

, n N.

Замечание 1. Если производная существует при каждом значении х в рассматриваемом промежутке, то она является функцией от х и обозначается f (x).

Замечание 2. Процесс нахождения производной функции называется

дифференцированием.

Рассмотрим геометрический смысл понятия производной.

Пусть в декартовой прямоугольной системе координат xOy задан

график функции		y f (x). Выберем на кривой точку					M0 x0, y0 и точку
M x0 x, y0	y	и проведем секущую			M0M , образующую с осью Oх
угол (рис.5.2).
Определение 2. Пусть точка М приближается к точке M0								так, что рас-
стояние между ними			M0M 0. Если при этом			секущая		M0M будет
			l		приближатьcя к некоторому пре-
y			l		дельному положению M0T				так,
y			М		дельному положению M0T				так,
					что угол между прямыми M0M и
				Т	M0T стремится к нулю, то прямая
			Q	у	M0T называется касательной к
			Q	у	кривой в точке M0 .
					кривой в точке M0 .
			dу		Наличие		в точке M0		каса-
y0	М0				тельнойM0T ,		образующей с осью
y0			P		Ox ориентированный угол 0, эк-
			P		Ox ориентированный угол 0, эк-
			x		вивалентно равенству 0 lim ,
					вивалентно равенству 0 lim ,
								x 0
					а значит,	и	равенству		tg 0=
0					lim tg .
					x 0
О		x0	x0 + x	х	Очевидно, что имеет место
	Рис.5.2				равенство
46

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете Добыча нефти и газа

#
24.01.20211.08 Mб3Выбор параметров редуктора.pdf
#
03.01.20212.26 Mб6Выбор сечений жил кабельных линий.pdf
#
17.01.2021107.99 Кб3Выбор условий возбуждения колебаний при сейсморазведке МГТ 2Д в условиях Западно-прикаспийской впадины.pdf
#
24.01.2021762 Кб5Выбор электродвигателя, кинематический и силовой расчет привода.pdf
#
06.01.2021559.2 Кб4высокополярные нефти.pdf
#
03.01.20211.01 Mб15ВЫСШАЯ МАТЕМАТИКА_ГОРНЫЙ.pdf
#
06.01.2021233.22 Кб8вытеснении нефти.pdf
#
03.01.2021439.96 Кб4вытеснения нефти.pdf
#
31.01.20211.39 Mб3ВЯЗКОСТЬ.pdf
#
01.02.20211.21 Mб5Газгольдеры.pdf
#
03.02.20212.86 Mб23газоанализатор.pdf