
Вот это значение является абсолютно точным.
Погрешности рассчитываются по стандартным формулам, о которых уже шла речь в этой статье.
Абсолютная погрешность:
Относительная погрешность:
Ответ: ,
абсолютная погрешность:  , относительная погрешность:
, относительная погрешность:  .
.
Пример 9
Вычислить приближенное значение функции  в точке
в точке  с помощью полного дифференциала, оценить абсолютную и относительную погрешность.
с помощью полного дифференциала, оценить абсолютную и относительную погрешность.
Это пример для самостоятельного решения. Кто остановится подробнее на данном примере, тот обратит внимание на то, что погрешности вычислений получились весьма и весьма заметными. Это произошло по следующей причине: в предложенной задаче достаточно велики приращения
аргументов:  .
.
Общая закономерность такова – чем больше эти приращения по абсолютной величине, тем ниже точность вычислений. Так, например, для похожей точки  приращения будут
приращения будут
небольшими:  , и точность приближенных вычислений получится очень высокой.
, и точность приближенных вычислений получится очень высокой.
Данная особенность справедлива и для случая функции одной переменной (первая часть урока).
Пример 10 С помощью полного дифференциала функции двух переменных вычислить приближенно
значение данного выражения:
 .
.
Вычислить это же выражение с помощью микрокалькулятора. Оценить в процентах относительную погрешность вычислений.
Решение: Вычислим данное выражение приближенно с помощью полного дифференциала функции двух переменных:
 .
.
Отличие от Примеров 8-9 состоит в том, что нам сначала необходимо составить функцию двух
переменных:  .
.
Как составлена функция, думаю, всем интуитивно понятно.
Значение 4,9973 близко к «пятерке», поэтому:  ,
,  .
.
Значение 0,9919 близко к «единице», следовательно, полагаем:  ,
,  .
.
Вычислим значение функции в точке  :
:
Дифференциал в точке |
найдем по формуле: |
Для этого вычислим частные производные первого порядка в точке  . Производные здесь не самые простые, и следует быть аккуратным:
. Производные здесь не самые простые, и следует быть аккуратным:
.
.
Полный дифференциал в точке  :
:
Таким образом, приближенное значение данного выражения:
 .
.
Вычислим более точное значение с помощью микрокалькулятора: 2,998899527.
Найдем относительную погрешность вычислений:
 .
.
Ответ:  .
.  .
.
Как иллюстрация к вышесказанному, в рассмотренной задаче приращения аргументов очень малы  , и погрешность получилась фантастически мизерной.
, и погрешность получилась фантастически мизерной.
Пример 11 С помощью полного дифференциала функции двух переменных вычислить приближенно
значение данного выражения. Вычислить это же выражение с помощью микрокалькулятора. Оценить в процентах относительную погрешность вычислений.
 .
.
Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.
И заключительный простой пример:
Пример 12 С помощью полного дифференциала функции двух переменных вычислить приближенно
значение функции  , если
, если  . Решение смотрите ниже.
. Решение смотрите ниже.
Еще раз обратите внимание на формулировки заданий урока, в различных примерах на практике формулировки могут быть разными, но это принципиально не меняет сути и алгоритма решения. Задачи вычислительной математики обычно не очень сложны, не очень интересны. Самое важное здесь - не допустить ошибку в обычных расчётах.
Решения и ответы:
Пример 2: Решение: Используем формулу: 
В данном случае:  ,
,  ,
,  .
.
 .
.
Таким образом:  .
.
Ответ:  .
.
Пример 4: Решение: Используем формулу: 
В данном случае:  ,
,  ,
, 
Таким образом:  .
.
Вычислим более точное значение функции с помощью микрокалькулятора:
193
Абсолютная погрешность:
Относительная погрешность:
 .
.
Ответ:  , абсолютная погрешность вычислений
, абсолютная погрешность вычислений  , относительная погрешность вычислений
, относительная погрешность вычислений  .
.
Пример 5: Решение: Используем формулу:  .
.
В данном случае:  ,
,  ,
, 
 .
.
Таким образом:
Ответ:
 .
.
Пример 7: Решение: Используем формулу:  .
.
В данном случае:  ,
,  ,
,
 .
.
 .
.
Таким образом:  .
.
Ответ:  .
.
Пример 9: Решение: Используем формулу: 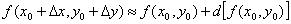 В данной задаче:
В данной задаче:
 ,
,  ,
,  ,
,  ,
,  .
.
Вычислим частные производные первого порядка в точке (2; 1):
 .
.
Полный дифференциал в точке (2; 1):  .
.
Таким образом:  .
.
С помощью калькулятора вычислим точное значение функции в данной точке:
Абсолютная погрешность:
 .
.
Относительная погрешность:
 .
.
Ответ:  ,
,
абсолютная погрешность:  , относительная погрешность:
, относительная погрешность:  .
.
Пример 11: Решение: С помощью полного дифференциала вычислим данное выражение приближенно:
 .
.
В данной задаче:
,  ,
,  ,
,  .
.
 .
.
 .
.
Вычислим частные производные первого порядка в точке (1; 1):
. .
.
.
Полный дифференциал в точке (1; 1):
Таким образом, приближенное значение данного выражения:
 .
.
Значение, вычисленное с помощью микрокалькулятора: 2,007045533.
Найдем относительную погрешность вычислений:
 .
.
Ответ:  ,
,  .
.
Пример 12: Решение: Используем формулу:  .
.
В данной задаче:  ,
,  ,
,  ,
,  ,
,  .
.
 .
.
 .
.
Вычислим частные производные первого порядка в точке (5; 0):
 .
.
Полный дифференциал в точке (5; 0):
 .
.
Таким образом:
 .
.
Ответ:  .
.
7.5. Частные производные функции трёх переменных
Продолжаем всеми любимую тему математического анализа – производные. В данной статье мы научимся находить частные производные функции трёх переменных: первые производные и вторые производные. Что необходимо знать и уметь для освоения материала? Не поверите, но, во-первых, нужно уметь находить «обычные» производные функции одной переменной – на высоком или хотя бы среднем уровне. Если с ними совсем туго, то начните с урока Производные функций одной переменной. Во-вторых, очень важно прочитать статью Частные производные функции двух переменных, осмыслить и прорешать если не все, то бОльшую часть примеров. Если это уже сделано, то пойдём уверенной походкой, будет интересно, даже удовольствие получите!
Методы и принципы нахождения частных производных функции трёх переменных на самом деле очень похожи на частные производные функции двух переменных. Функция двух переменных, напоминаю, имеет вид z = f(x; y), где «икс» и «игрек» – независимые переменные. Геометрически функция двух переменных представляет собой некоторую поверхность в нашем трёхмерном пространстве.
Функция трёх переменных имеет вид u = f(x; y; z), при этом переменные x; y; z называются
независимыми переменными или аргументами, а переменная u называется зависимой переменной или функцией. Например:
 – это функция трёх переменных.
– это функция трёх переменных.

А теперь немного о фантастических фильмах и инопланетянах. Часто можно услышать о четырехмерном, пятимерном, десятимерном и т.д. пространствах. Чушь это или нет?
Ведь функция трёх переменных  подразумевает тот факт, что все дела происходят в четырехмерном пространстве (действительно, переменных же четыре). График функции трёх переменных представляет собой так называемую гиперповерхность.
подразумевает тот факт, что все дела происходят в четырехмерном пространстве (действительно, переменных же четыре). График функции трёх переменных представляет собой так называемую гиперповерхность.
Представить её невозможно, поскольку мы живём в трехмерном пространстве (длина / ширина / высота). Чтобы вам со мной не было скучно, предлагаю викторину. Я задам несколько вопросов, а желающие могут попробовать на них ответить:
–Существует ли в мире четвертое, пятое и т.д. измерения в смысле обывательского понимания пространства (длина / ширина / высота)?
–Можно ли построить четырехмерное, пятимерное и т.д. пространство в широком понимании этого слова? То есть, привести пример такого пространства в нашей жизни.
–Возможно ли путешествие в прошлое?
–Возможно ли путешествие в будущее?
–Существуют ли инопланетяне?
На любой вопрос можно выбрать один из четырёх ответов:
Да / Нет (наукой это запрещено) / Наукой это не запрещено / Не знаю Кто правильно ответит на все вопросы, тот, скорее всего, обладает некоторой вещью ☺.
Ответы на вопросы я постепенно буду выдавать по ходу урока, не пропускайте примеры! Собственно, полетели. И сразу хорошая новость: для функции трёх переменных справедливы правила дифференцирования и таблица производных. Именно поэтому вам необходимо хорошо управляться с «обычными» производными функций одной переменной. Отличий совсем немного!
Пример 1 Найти частные производные первого порядка функции трёх переменных
Решение: Нетрудно догадаться, что для функции трёх переменных существуют три частных производных первого порядка, которые обозначаются следующим образом:
 или
или  – частная производная по «икс»;
– частная производная по «икс»;
 или
или  – частная производная по «игрек»;
– частная производная по «игрек»;
 или
или  – частная производная по «зет».
– частная производная по «зет».
В ходу больше обозначение со штрихом, но составители сборников и методичек в условиях задач очень любят использовать как раз громоздкие обозначения – так что не теряйтесь! Возможно, не все знают, как правильно читать вслух эти «страшные дроби с круглыми дэ»?
Пример:  следует читать следующим образом: «частная производная дэ у по дэ икс».
следует читать следующим образом: «частная производная дэ у по дэ икс».
Начнём с производной « у по икс»:  . Когда мы находим частную производную по
. Когда мы находим частную производную по  , то переменные
, то переменные  и
и 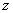 считаются константами (постоянными числами). А производная любой константы, как известно, равна нулю:
считаются константами (постоянными числами). А производная любой константы, как известно, равна нулю:

Сразу обратите внимание на подстрочный индекс  – никто вам не запрещает помечать, что
– никто вам не запрещает помечать, что  являются константами. Так даже удобнее, начинающим рекомендую использовать именно такую запись, меньше риск запутаться.
являются константами. Так даже удобнее, начинающим рекомендую использовать именно такую запись, меньше риск запутаться.
(1) Используем свойства линейности производной, в частности, выносим все константы за знак производной. Обратите внимание, что во втором слагаемом  константу выносить не нужно:
константу выносить не нужно:
так как «игрек» является константой, то  – тоже константа. В слагаемом
– тоже константа. В слагаемом  за знак производной вынесена «обычная» константа 8 и константа «зет».
за знак производной вынесена «обычная» константа 8 и константа «зет».
(2) Находим простейшие производные, не забывая при этом, что  – константы. Далее причесываем ответ.
– константы. Далее причесываем ответ.
Частная производная  . Когда мы находим частную производную «у по игрек», то
. Когда мы находим частную производную «у по игрек», то
переменные  и
и  считаются константами:
считаются константами:
(1) Используем свойства линейности. И снова заметьте, что слагаемые |
, |
являются |
константами, а значит, за знак производной выносить ничего не нужно. |
|
|
(2) Находим производные, не забывая, что  константы. Далее упрощаем ответ.
константы. Далее упрощаем ответ.
И, наконец, частная производная  . Когда мы находим частную производную по «у по зет»,
. Когда мы находим частную производную по «у по зет»,
то переменные  и
и  считаются константами:
считаются константами:
Общее правило очевидно и незатейливо: «Когда мы находим частную производную по какойлибо независимой переменной, то две другие независимые переменные считаются константами».
При оформлении данных задач следует быть предельно внимательным, в частности, нельзя терять подстрочные индексы (которые указывают, по какой переменной проводится дифференцирование). Потеря индекса будет ГРУБЫМ НЕДОЧЁТОМ.
Пример 2 Найти частные производные первого порядка функции трёх переменных
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Рассмотренные два примера достаточно просты и, решив несколько подобных задачек, даже чайник приноровится расправляться с ними устно.
Для разгрузки вернемся к первому вопросу викторины: Существует ли в мире четвертое, пятое и т.д. измерения в смысле обывательского понимания пространства (длина / ширина / высота)?
Верный ответ: «Наукой это не запрещено». Вся фундаментальная математическая аксиоматика, теоремы, математический аппарат прекрасно и непротиворечиво работают в пространстве любой размерности. Не исключено, что где-нибудь во Вселенной существуют неподвластные нашему разуму гиперповерхности, например, четырёхмерная гиперповерхность, которая
задается функцией трех переменных  . А может быть, гиперповерхности рядом с нами или даже мы находимся прямо в них, просто наше зрение, другие органы чувств и сознание способны на восприятие и осмысление только трёх измерений.
. А может быть, гиперповерхности рядом с нами или даже мы находимся прямо в них, просто наше зрение, другие органы чувств и сознание способны на восприятие и осмысление только трёх измерений.

Вернемся к примерам. Помимо простейших Примеров 1-2 на практике встречаются задания, которые можно назвать небольшой головоломкой. Навёрстываем упущенное.
Пример 3 Найти частные производные первого порядка функции трёх переменных и составить полный
дифференциал первого порядка
 .
.
Решение: вроде бы тут «всё просто», но первое впечатление обманчиво. При нахождении частных производных многие будут гадать на кофейной гуще и ошибаться.
Разберём пример последовательно, чётко и понятно.
Начнём с частной производной по «икс». Когда мы находим частную производную по «икс», то переменные y, z считаются константами. Следовательно, показатель нашей функции yz – тоже константа. Для чайников рекомендую следующий приём решения: на черновике поменяйте константу yz на конкретное положительное целое число, например, на «пятерку». В результате получится функция одной переменной:
 ; или ещё можно записать так:
; или ещё можно записать так:  .
.
Это степенная функция со сложным основанием (синусом). По правилу дифференцирования сложной функции:
 Теперь вспоминаем, что
Теперь вспоминаем, что
 , таким образом:
, таким образом:  .
.
На чистовике, конечно, решение следует оформить так:
Находим частную производную по «игрек», тогда x, z считаются константами. Если «икс»
константа, то  – тоже константа. На черновике проделываем тот же трюк:
– тоже константа. На черновике проделываем тот же трюк:  заменим, например, на 3, «зет» – заменим той же «пятёркой». В результате снова получается функция одной переменной:
заменим, например, на 3, «зет» – заменим той же «пятёркой». В результате снова получается функция одной переменной:
 .
.
Это показательная функция со сложным показателем. По правилу дифференцирования сложной функции:
 .
.
Теперь вспоминаем нашу замену:  .
.
Таким образом: 
На чистовике, понятно, оформление должно выглядеть, благообразно:
И зеркальный случай с частной производной по «зет» (x, y – константы):
При определенном опыте проведенный анализ можно проводить мысленно.
Выполняем вторую часть задания – составим дифференциал первого порядка. Это очень просто, по аналогии с функцией двух переменных, дифференциал первого порядка записывается по формуле:
В данном случае:
Пример 4 Найти частные производные первого порядка для функции трёх переменных
и составить полный дифференциал первого порядка.
Полное решение и ответ в конце урока. Если возникнут затруднения, используйте рассмотренный «чайниковский» алгоритм, он гарантированно должен помочь. И ещё полезный совет – не спешите. Такие примеры быстро не решаю даже я.
Отвлекаемся и разбираем второй вопрос викторины: «Можно ли построить четырехмерное, пятимерное и т.д. пространство в широком понимании этого слова?». То есть, привести пример такого пространства в нашей жизни.
Верный ответ: Да. Причём, очень легко. Например, добавляем к (длине / ширине / высоте)
четвёртое измерение – время.
К рассмотренному четырехмерному пространству легко добавить пятое измерение, например: атмосферное давление. И так далее, и так далее, и так далее, сколько зададите измерений в своей модели – столько и будет. В широком смысле слова мы живём в многомерном пространстве.
Разберём еще пару типовых задач:
Пример 5
Найти частные производные первого порядка в точке M(2, 1, 0) для функции:
 .
.
Решение: Задание в такой формулировке часто встречается на практике и предполагает выполнение следующих двух действий:
–нужно найти частные производные первого порядка;
–нужно вычислить значения частных производных 1-го порядка в точке M(2, 1, 0). Решаем:
(1) Перед нами сложная функция, и на первом шаге следует взять производную от арктангенса. При этом мы, по сути, невозмутимо используем табличную формулу производной арктангенса
 .
.
По правилу дифференцирования сложной функции результат необходимо домножить на производную внутренней функции (вложения):
 .
.
(2)Используем свойства линейности.
(3)И берём оставшиеся производные, не забывая, что y, z – константы.
По условию задания необходимо найти значение найденной частной производной
в точке M(2, 1, 0). Подставим координаты точки в найденную производную:
.
Преимуществом данного задания является тот факт, что другие частные производные находятся по очень похожей схеме:
200




 , если
, если  . Решение смотрите ниже.
. Решение смотрите ниже.
 ,
,  ,
,  .
. .
. .
. .
.
 ,
,  ,
, 
 .
.





 .
. .
. .
.
 , относительная погрешность:
, относительная погрешность:  .
. в точке
в точке  с помощью полного дифференциала, оценить абсолютную и относительную погрешность.
с помощью полного дифференциала, оценить абсолютную и относительную погрешность. .
. приращения будут
приращения будут , и точность приближенных вычислений получится очень высокой.
, и точность приближенных вычислений получится очень высокой. .
. .
. .
. ,
,  .
. ,
,  .
. :
: . Производные здесь не самые простые, и следует быть аккуратным:
. Производные здесь не самые простые, и следует быть аккуратным: :
: .
. .
.

 , и погрешность получилась фантастически мизерной.
, и погрешность получилась фантастически мизерной. .
. .
. , абсолютная погрешность вычислений
, абсолютная погрешность вычислений  , относительная погрешность вычислений
, относительная погрешность вычислений  .
. .
. ,
,  ,
, 
 .
. .
. .
. ,
,  ,
, .
. .
. .
.
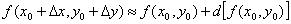 В данной задаче:
В данной задаче: ,
,  ,
,  ,
,  ,
,  .
. .
. .
. .
. .
. .
.
 , относительная погрешность:
, относительная погрешность:  .
. .
. ,
,  ,
,  .
. .
. .
. .
. .
. .
.

 .
. ,
,  ,
,  ,
,  ,
,  .
. .
. .
. .
. .
. .
.
 – это функция трёх переменных.
– это функция трёх переменных. подразумевает тот факт, что все дела происходят в четырехмерном пространстве (действительно, переменных же четыре). График функции трёх переменных представляет собой так называемую
подразумевает тот факт, что все дела происходят в четырехмерном пространстве (действительно, переменных же четыре). График функции трёх переменных представляет собой так называемую  или
или  – частная производная по «икс»;
– частная производная по «икс»; или
или  – частная производная по «игрек»;
– частная производная по «игрек»; или
или  – частная производная по «зет».
– частная производная по «зет». следует читать следующим образом: «частная производная дэ у по дэ икс».
следует читать следующим образом: «частная производная дэ у по дэ икс».
 , то переменные
, то переменные  и
и 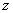 считаются константами (постоянными числами).
считаются константами (постоянными числами).  – никто вам не запрещает помечать, что
– никто вам не запрещает помечать, что  являются константами. Так даже удобнее, начинающим рекомендую использовать именно такую запись, меньше риск запутаться.
являются константами. Так даже удобнее, начинающим рекомендую использовать именно такую запись, меньше риск запутаться. константу выносить не нужно:
константу выносить не нужно: – тоже константа. В слагаемом
– тоже константа. В слагаемом  за знак производной вынесена «обычная» константа 8 и константа «зет».
за знак производной вынесена «обычная» константа 8 и константа «зет». – константы. Далее причесываем ответ.
– константы. Далее причесываем ответ.
 и
и  считаются константами:
считаются константами: константы. Далее упрощаем ответ.
константы. Далее упрощаем ответ.
 и
и  считаются константами:
считаются константами: . А может быть, гиперповерхности рядом с нами или даже мы находимся прямо в них, просто наше зрение, другие органы чувств и сознание способны на восприятие и осмысление только трёх измерений.
. А может быть, гиперповерхности рядом с нами или даже мы находимся прямо в них, просто наше зрение, другие органы чувств и сознание способны на восприятие и осмысление только трёх измерений. .
. ; или ещё можно записать так:
; или ещё можно записать так:  .
. Теперь вспоминаем, что
Теперь вспоминаем, что , таким образом:
, таким образом:  .
. – тоже константа. На черновике проделываем тот же трюк:
– тоже константа. На черновике проделываем тот же трюк:  заменим, например, на 3, «зет» – заменим той же «пятёркой». В результате снова получается функция одной переменной:
заменим, например, на 3, «зет» – заменим той же «пятёркой». В результате снова получается функция одной переменной: .
. .
. .
.