
Пример 2
Найти частные производные первого и второго порядка функции  Это пример для самостоятельного решения (ответ в конце урока).
Это пример для самостоятельного решения (ответ в конце урока).
При определенном опыте частные производные из примеров №№1,2 будут решаться Вами устно.
Переходим к более сложным примерам.
Пример 3
Найти частные производные первого порядка функции  . Проверить, что
. Проверить, что  .
.
Записать полный дифференциал первого порядка  . Решение: Находим частные производные первого порядка:
. Решение: Находим частные производные первого порядка:
Обратите внимание на подстрочный индекс: |
, рядом с «иксом» не возбраняется в |
скобках записывать, что  – константа. Данная пометка может быть очень полезна для начинающих, чтобы легче было ориентироваться в решении.
– константа. Данная пометка может быть очень полезна для начинающих, чтобы легче было ориентироваться в решении.
Дальнейшие комментарии:
(1) Выносим все константы за знак производной. В данном случае  и
и  , а, значит, и их
, а, значит, и их
произведение  считается постоянным числом.
считается постоянным числом.
(2) Не забываем, как правильно дифференцировать корни.
(1)Выносим все константы за знак производной, в данной случае константой является  .
.
(2)Под штрихом у нас осталось произведение двух функций, следовательно, нужно
использовать правило дифференцирования произведения  .
.
(3) Не забываем, что  – это сложная функция (хотя и простейшая из сложных).
– это сложная функция (хотя и простейшая из сложных).
Используем соответствующее правило:  . Теперь находим смешанные производные второго порядка:
. Теперь находим смешанные производные второго порядка:
, значит, все вычисления выполнены верно.
Запишем полный дифференциал  . В контексте рассматриваемого задания не имеет смысла рассказывать, что такое полный дифференциал функции двух переменных. Важно, что этот самый дифференциал очень часто требуется записать в практических задачах.
. В контексте рассматриваемого задания не имеет смысла рассказывать, что такое полный дифференциал функции двух переменных. Важно, что этот самый дифференциал очень часто требуется записать в практических задачах.
Полный дифференциал первого порядка функции двух переменных имеет вид:
 .
.
В данном случае:
То есть, в формулу нужно просто подставить уже найденные частные производные первого
порядка. Значки дифференциалов  и
и  в этой и похожих ситуациях по возможности лучше записывать в числителях:
в этой и похожих ситуациях по возможности лучше записывать в числителях:
Пример 4
Найти частные производные первого порядка функции  . Проверить, что
. Проверить, что
 . Записать полный дифференциал первого порядка
. Записать полный дифференциал первого порядка  .
.
Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Рассмотрим серию примеров, включающих в себя сложные функции.
Пример 5
Найти частные производные первого порядка функции  .
.
Записать полный дифференциал  . Решение:
. Решение:
(1) Применяем правило дифференцирования сложной функции  . С урока Производная сложной функции следует помнить очень важный момент: когда мы по таблице
. С урока Производная сложной функции следует помнить очень важный момент: когда мы по таблице
превращаем синус (внешнюю функцию) в косинус, то вложение |
(внутренняя функция) у |
нас не меняется. |
|
|
182 |

(2) Здесь используем свойство корней:  , выносим константу
, выносим константу  за знак производной, а корень
за знак производной, а корень  представляем в нужном для дифференцирования виде.
представляем в нужном для дифференцирования виде.
Аналогично: Запишем полный дифференциал первого
Запишем полный дифференциал первого
порядка:
Пример 6
Найти частные производные первого порядка функции  .
.
Записать полный дифференциал  .
.
Это пример для самостоятельного решения (ответ в конце урока). Полное решение не привожу, так как оно достаточно простое Довольно часто все вышерассмотренные правила применяются в комбинации.
Пример 7
Найти частные производные первого порядка функции  .
.
(1)Используем правило дифференцирования суммы.
(2)Первое слагаемое в данном случае считается константой, поскольку в выражении  нет ничего, зависящего от «икс» – только «игреки».
нет ничего, зависящего от «икс» – только «игреки».
(Знаете, всегда приятно, когда дробь удается превратить в ноль).
Для второго слагаемого применяем правило дифференцирования произведения. Кстати, в
алгоритме ничего бы не изменилось, если бы вместо  была дана функция
была дана функция  – важно, что здесь мы имеем произведение двух функций, КАЖДАЯ из которых зависит от
– важно, что здесь мы имеем произведение двух функций, КАЖДАЯ из которых зависит от
«икс», поэтому нужно использовать правило дифференцирования произведения. Для третьего слагаемого применяем правило дифференцирования сложной функции.
Найдем теперь частную производную по y:
(1) В первом слагаемом и в числителе и в знаменателе содержится «игрек», следовательно,
нужно использовать правило дифференцирования частного:  . Второе слагаемое
. Второе слагаемое
зависит ТОЛЬКО от «икс», значит,  считается константой и превращается в ноль. Для третьего слагаемого используем правило дифференцирования сложной функции.
считается константой и превращается в ноль. Для третьего слагаемого используем правило дифференцирования сложной функции.
Для тех читателей, которые мужественно добрались почти до конца урока, расскажу старый мехматовский анекдот для разрядки.
Однажды в пространстве функций появилась злобная производная и как пошла всех дифференцировать. Все функции разбегаются кто куда, никому не хочется превращаться! И только одна функция никуда не убегает. Подходит к ней производная и спрашивает:
–А почему это ты от меня никуда не убегаешь?
–Ха. А мне всё равно, ведь я «е в степени икс», и ты со мной ничего не сделаешь! На что злобная производная с коварной улыбкой отвечает:
–Вот здесь ты ошибаешься, я тебя продифференцирую по «игрек», так что быть тебе нулем.
(Кто понял анекдот, тот освоил производные, минимум, на «тройку»).
Пример 8
Найти частные производные первого порядка функции  . Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
. Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Пример 9
Дана функция двух переменных  . Найти все частные производные первого и второго порядков.
. Найти все частные производные первого и второго порядков.
Это пример для самостоятельного решения. Полное решение и образец оформления где-то рядом.
Решения и ответы:
Пример 2:
 ,
,  ,
,  ,
,
Пример 4: Ссылка для просмотра ниже.
Пример 6:
184
 ,
,  ,
,
7.4. Приближенные вычисления с помощью дифференциала
Рассмотрим широко распространенную задачу о приближенном вычислении значения функции с помощью дифференциала.
Здесь и далее речь пойдёт о дифференциалах первого порядка, для краткости часто будем говорить просто «дифференциал». Задача о приближенных вычислениях с помощью дифференциала обладает жёстким алгоритмом решения, и, следовательно, особых трудностей возникнуть не должно. Единственное, есть небольшие подводные камни, которые тоже будут подчищены. Так что смело ныряйте головой вниз.
Кроме того, в разделе присутствуют формулы нахождения абсолютной и относительной погрешностей вычислений. Материал очень полезный, поскольку погрешности приходится рассчитывать и в других задачах.
Для успешного освоения примеров необходимо уметь находить производные функций хотя бы на среднем уровне, поэтому если с дифференцированием совсем нелады, пожалуйста, начните с
нахождения производной в точке и с нахождения дифференциала в точке. Из технических средств потребуется микрокалькулятор с различными математическими функциями. Можно использовать возможности MS Excel, но в данном случае он менее удобен.
Урок состоит из двух частей:
–Приближенные вычисления с помощью дифференциала значения функции одной переменной в точке.
–Приближенные вычисления с помощью полного дифференциала значения функции двух переменных в точке.
Рассматриваемое задание тесно связано с понятием дифференциала, но, поскольку урока о смысле производной и дифференциала у нас пока нет, ограничимся формальным рассмотрением примеров, чего вполне достаточно, чтобы научиться их решать.
Приближенные вычисления с помощью дифференциала функции одной переменной
В первом параграфе рулит функция одной переменной. Как все знают, она обозначается через y или через f(x). Для данной задачи намного удобнее использовать второе обозначение. Сразу перейдем к популярному примеру, который часто встречается на практике:
Пример 1
Вычислить приближенно  , заменяя приращения функции ее дифференциалом. Решение: Пожалуйста, перепишите в тетрадь рабочую формулу для приближенного вычисления с помощью дифференциала:
, заменяя приращения функции ее дифференциалом. Решение: Пожалуйста, перепишите в тетрадь рабочую формулу для приближенного вычисления с помощью дифференциала:
Начинаем разбираться, здесь всё просто!
На первом этапе необходимо составить функцию  . По условию предложено вычислить кубический корень из числа:
. По условию предложено вычислить кубический корень из числа:  , поэтому соответствующая функция имеет вид:
, поэтому соответствующая функция имеет вид:  .
.
Нам нужно с помощью формулы найти приближенное значение  .
.
185

Смотрим на левую часть формулы  , и в голову приходит мысль,
, и в голову приходит мысль,
что число 67 необходимо представить в виде 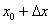 . Как проще всего это сделать? Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе:
. Как проще всего это сделать? Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе:
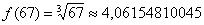 – получилось 4 с хвостиком, это важный ориентир для решения.
– получилось 4 с хвостиком, это важный ориентир для решения.
Вкачестве x0 подбираем «хорошее» значение, чтобы корень извлекался нацело. Естественно, это значение x0 должно быть как можно ближе к 67.
Вданном случае x0 = 64. Действительно,  .
.
Примечание: Когда с подбором x0 всё равно возникает затруднение, просто посмотрите на скалькулированное значение (в данном случае  ), возьмите ближайшую целую
), возьмите ближайшую целую
часть (в данном случае 4) и возведите её нужную в степень (в данном случае 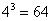 ). В результате и будет выполнен нужный подбор x0 = 64.
). В результате и будет выполнен нужный подбор x0 = 64.
Если x0 = 64, то приращение аргумента:  .
.
Итак, число 67 представлено в виде суммы 
Далее работаем с правой частью формулы  .
.
Сначала вычислим значение функции в точке x0 = 64. Собственно, это уже сделано ранее:
 .
.
Дифференциал в точке находится по формуле:
 – эту формулу тоже можете переписать к себе в тетрадь. Из формулы следует, что нужно взять первую производную:
– эту формулу тоже можете переписать к себе в тетрадь. Из формулы следует, что нужно взять первую производную:
И найти её значение в точке x0:
 .
.
Таким образом:
Всё готово! Согласно формуле |
: |
Найденное приближенное значение достаточно близко к значению 4,06154810045, вычисленному с помощью микрокалькулятора.
Ответ: 
Пример 2
Вычислить приближенно  , заменяя приращения функции ее дифференциалом.
, заменяя приращения функции ее дифференциалом.
Это пример для самостоятельного решения. Примерный образец чистового оформления и ответ
в конце урока. Начинающим сначала рекомендую вычислить точное значение  на микрокалькуляторе, чтобы выяснить, какое число принять за x0, а какое – за x. Следует отметить, что x в данном примере будет отрицательным.
на микрокалькуляторе, чтобы выяснить, какое число принять за x0, а какое – за x. Следует отметить, что x в данном примере будет отрицательным.
У некоторых, возможно, возник вопрос, зачем нужна эта задача, если можно всё спокойно и более точно подсчитать на калькуляторе? Согласен, задача глупая и наивная. Но попытаюсь немного её оправдать. Во-первых, задание иллюстрирует смысл дифференциала функции. Вовторых, в древние времена калькулятор был чем-то вроде личного вертолета в наше время. Сам

видел, как из одного из институтов году где-то в 1985-86 выбросили компьютер размером с комнату (со всего города сбежались радиолюбители с отвертками, и через пару часов от агрегата остался только корпус). Антиквариат водился и у нас на физфаке, правда, размером поменьше – где-то с парту. Вот так вот и мучились наши предки с методами приближенных вычислений. Конная повозка – тоже транспорт.
Так или иначе, задача осталась в стандартном курсе высшей математики, и решать её придётся. Это основной ответ на ваш вопрос =).
Пример 3
Вычислить приближенно с помощью дифференциала значение функции  в точке x = 1,97. Вычислить более точное значение функции в точке x = 1,97 с помощью микрокалькулятора, оценить абсолютную и относительную погрешность вычислений. Фактически, это задание запросто можно переформулировать так: «Вычислить приближенное
в точке x = 1,97. Вычислить более точное значение функции в точке x = 1,97 с помощью микрокалькулятора, оценить абсолютную и относительную погрешность вычислений. Фактически, это задание запросто можно переформулировать так: «Вычислить приближенное
значение  с помощью дифференциала»
с помощью дифференциала»
Решение: Используем знакомую формулу: |
|
В данном случае уже дана готовая функция: |
. Ещё раз обращаю внимание, |
что для обозначения функции вместо «игрека» удобнее использовать f(x). |
Значение x = 1,97 необходимо представить в виде x0 = |
x. Ну, тут легче, мы видим, что число |
1,97 очень близко к «двойке», поэтому напрашивается x0 = 2. И, следовательно:  . Вычислим значение функции в точке x0 = 2:
. Вычислим значение функции в точке x0 = 2:
Используя формулу Находим первую производную:
И её значение в точке x0 = 2:
Таким образом, дифференциал в точке:
В результате, по формуле
, вычислим дифференциал в этой же точке.
:
Вторая часть задания состоит в том, чтобы найти абсолютную и относительную погрешность вычислений.
Абсолютная и относительная погрешности вычислений
Абсолютная погрешность вычислений находится по формуле:
Знак модуля показывает, что нам без разницы, какое значение больше, а какое меньше. Важно, насколько далеко приближенный результат отклонился от точного значения в ту или иную сторону.
Относительная погрешность вычислений находится по формуле:

 , или, то же самое:
, или, то же самое:
Относительная погрешность показывает, на сколько процентов приближенный результат отклонился от точного значения. Существует версия формулы и без умножения на 100%, но на практике почти всегда используют вышеприведенный вариант с процентами.
После короткой справки вернемся к нашей задаче, в которой мы вычислили приближенное
значение функции  с помощью дифференциала. Вычислим точное значение функции с помощью микрокалькулятора:
с помощью дифференциала. Вычислим точное значение функции с помощью микрокалькулятора:
 , строго говоря, значение всё равно приближенное, но мы будем считать его точным. Такие уж задачи встречаются.
, строго говоря, значение всё равно приближенное, но мы будем считать его точным. Такие уж задачи встречаются.
Вычислим абсолютную погрешность:
Вычислим относительную погрешность:
 , получены тысячные доли процента, таким образом, дифференциал обеспечил просто отличное приближение.
, получены тысячные доли процента, таким образом, дифференциал обеспечил просто отличное приближение.
Ответ:  , абсолютная погрешность вычислений
, абсолютная погрешность вычислений  , относительная
, относительная
погрешность вычислений  . Следующий пример для самостоятельного решения:
. Следующий пример для самостоятельного решения:
Пример 4
Вычислить приближенно с помощью дифференциала значение функции  в
в
точке  . Вычислить более точное значение функции в данной точке, оценить абсолютную и относительную погрешность вычислений.
. Вычислить более точное значение функции в данной точке, оценить абсолютную и относительную погрешность вычислений.
Примерный образец чистового оформления и ответ в конце урока.
Многие обратили внимание, что во всех рассмотренных примерах фигурируют корни. Это не случайно, в большинстве случаев в рассматриваемой задаче действительно предлагаются функции с корнями.
Но для страждущих читателей я раскопал небольшой пример с арксинусом:
Пример 5 Вычислить приближенно с помощью дифференциала значение функции  ; в точке
; в точке
 .
.
Этот коротенький, но познавательный пример тоже для самостоятельного решения.
Теперь рассмотрим особое задание:
Пример 6
Вычислить приближенно с помощью дифференциала  , результат округлить до двух знаков после запятой.
, результат округлить до двух знаков после запятой.
Решение: Что нового в задании? По условию требуется округлить результат до двух знаков после запятой. Но дело не в этом, школьная задача округления, думаю, не представляет для вас сложностей. Дело в том, что у нас дан тангенс с аргументом, который выражен в градусах.
Что делать, когда вам предлагается для решения тригонометрическая функция с градусами?
Например,  и т. д.
и т. д.
Алгоритм решения принципиально сохраняется, то есть необходимо, как и в предыдущих примерах, применить формулу  Записываем очевидную функцию
Записываем очевидную функцию 
Значение  нужно представить в виде
нужно представить в виде  . Серьёзную помощь окажет таблица значений тригонометрических функций. Кстати, кто её не распечатал, рекомендую это сделать, поскольку заглядывать туда придется на протяжении всего курса изучения высшей математики. Анализируя таблицу, замечаем «хорошее» значение тангенса, которое близко располагается к
. Серьёзную помощь окажет таблица значений тригонометрических функций. Кстати, кто её не распечатал, рекомендую это сделать, поскольку заглядывать туда придется на протяжении всего курса изучения высшей математики. Анализируя таблицу, замечаем «хорошее» значение тангенса, которое близко располагается к
47 градусам, а именно:  . Таким образом:
. Таким образом:  .
.
После предварительного анализа градусы необходимо перевести в радианы. Так, и только так!
В данном примере непосредственно из тригонометрической таблицы можно выяснить, что
 . По формуле перевода градусов в радианы:
. По формуле перевода градусов в радианы:  (формулы можно найти в той же таблице). Дальнейшее шаблонно:
(формулы можно найти в той же таблице). Дальнейшее шаблонно:
 .
.
Таким образом:  (при вычислениях используем значение
(при вычислениях используем значение  ). Результат, как и требовалось по условию, округлён до двух знаков после запятой.
). Результат, как и требовалось по условию, округлён до двух знаков после запятой.
Ответ:  .
.
Пример 7
Вычислить приближенно с помощью дифференциала  , результат округлить до трёх знаков после запятой.
, результат округлить до трёх знаков после запятой.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Как видите, ничего сложного, градусы переводим в радианы и придерживаемся обычного алгоритма решения.
Приближенные вычисления с помощью полного дифференциала функции двух переменных

Всё будет очень и очень похоже, поэтому, если вы зашли на эту страницу именно этим заданием, то сначала рекомендуем просмотреть хотя бы пару примеров предыдущего пункта. Для изучения параграфа необходимо уметь находить частные производные второго порядка, куда ж без них. На вышеупомянутом уроке функция двух переменных обозначена через букву  . Применительно к рассматриваемому заданию удобнее использовать эквивалентное
. Применительно к рассматриваемому заданию удобнее использовать эквивалентное
обозначение  .
.
Как и для случая функции одной переменной, условие задачи может быть сформулировано поразному, и мы постараемся рассмотреть все встречающиеся формулировки.
Пример 8
Вычислить приближенное значение функции  в точке
в точке  с помощью полного дифференциала, оценить абсолютную и относительную погрешность. Решение: Как бы ни было записано условие, в самом решении для обозначения функции,
с помощью полного дифференциала, оценить абсолютную и относительную погрешность. Решение: Как бы ни было записано условие, в самом решении для обозначения функции,
повторюсь, лучше использовать не букву «зет», а  . А вот и рабочая формула:
. А вот и рабочая формула:
Перед нами фактически старшая сестра формулы
предыдущего параграфа. Переменная только прибавилась. Сам же алгоритм решения будет
принципиально таким же.
По условию требуется найти приближенное значение функции в точке  .
.
Число 3,04 представим в виде  . Здесь, очевидно:
. Здесь, очевидно:
 ,
, 
Число 3,95 представим в виде  , что верно при:
, что верно при:
 ,
,  .
.
Вычислим значение функции в точке  :
:
Дифференциал функции в точке |
найдём по формуле: |
Из формулы следует, что нужно найти частные производные первого порядка и вычислить их значения в точке  .
.
Вычислим частные производные первого порядка в точке  :
:
Полный дифференциал в точке |
: |
Таким образом, по формуле
приближенное значение функции в точке  :
:
Вычислим точное значение функции в точке  :
:


 Это пример для самостоятельного решения (ответ в конце урока).
Это пример для самостоятельного решения (ответ в конце урока). . Проверить, что
. Проверить, что  .
. . Решение: Находим частные производные первого порядка:
. Решение: Находим частные производные первого порядка: – константа. Данная пометка может быть очень полезна для начинающих, чтобы легче было ориентироваться в решении.
– константа. Данная пометка может быть очень полезна для начинающих, чтобы легче было ориентироваться в решении. и
и  , а, значит, и их
, а, значит, и их считается постоянным числом.
считается постоянным числом. .
. .
. – это сложная функция (хотя и простейшая из сложных).
– это сложная функция (хотя и простейшая из сложных). . Теперь находим смешанные производные второго порядка:
. Теперь находим смешанные производные второго порядка:
 . В контексте рассматриваемого задания не имеет смысла рассказывать, что такое полный дифференциал функции двух переменных. Важно, что этот самый дифференциал очень часто требуется записать в практических задачах.
. В контексте рассматриваемого задания не имеет смысла рассказывать, что такое полный дифференциал функции двух переменных. Важно, что этот самый дифференциал очень часто требуется записать в практических задачах. .
. и
и  в этой и похожих ситуациях по возможности лучше записывать в числителях:
в этой и похожих ситуациях по возможности лучше записывать в числителях: . Проверить, что
. Проверить, что . Записать полный дифференциал первого порядка
. Записать полный дифференциал первого порядка  .
. .
. . Решение:
. Решение: . С урока Производная сложной функции следует помнить очень важный момент: когда мы по таблице
. С урока Производная сложной функции следует помнить очень важный момент: когда мы по таблице
 , выносим константу
, выносим константу  за знак производной, а корень
за знак производной, а корень  представляем в нужном для дифференцирования виде.
представляем в нужном для дифференцирования виде. Запишем полный дифференциал первого
Запишем полный дифференциал первого .
. .
. .
. нет ничего, зависящего от «икс» – только «игреки».
нет ничего, зависящего от «икс» – только «игреки». была дана функция
была дана функция  – важно, что здесь мы имеем произведение двух функций, КАЖДАЯ из которых зависит от
– важно, что здесь мы имеем произведение двух функций, КАЖДАЯ из которых зависит от
 . Второе слагаемое
. Второе слагаемое считается константой и превращается в ноль. Для третьего слагаемого используем правило дифференцирования сложной функции.
считается константой и превращается в ноль. Для третьего слагаемого используем правило дифференцирования сложной функции. . Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
. Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока. . Найти все частные производные первого и второго порядков.
. Найти все частные производные первого и второго порядков. ,
,  ,
,  ,
,
 ,
,  ,
, , заменяя приращения функции ее дифференциалом. Решение: Пожалуйста, перепишите в тетрадь рабочую формулу для приближенного вычисления с помощью дифференциала:
, заменяя приращения функции ее дифференциалом. Решение: Пожалуйста, перепишите в тетрадь рабочую формулу для приближенного вычисления с помощью дифференциала: . По условию предложено вычислить кубический корень из числа:
. По условию предложено вычислить кубический корень из числа:  , поэтому соответствующая функция имеет вид:
, поэтому соответствующая функция имеет вид:  .
. .
.




 , и в голову приходит мысль,
, и в голову приходит мысль,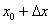 . Как проще всего это сделать? Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе:
. Как проще всего это сделать? Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе: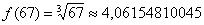 – получилось 4 с хвостиком, это важный ориентир для решения.
– получилось 4 с хвостиком, это важный ориентир для решения. .
. ), возьмите ближайшую целую
), возьмите ближайшую целую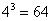 ). В результате и будет выполнен нужный подбор x
). В результате и будет выполнен нужный подбор x .
.
 .
. .
. – эту формулу тоже можете переписать к себе в тетрадь. Из формулы следует, что нужно взять первую производную:
– эту формулу тоже можете переписать к себе в тетрадь. Из формулы следует, что нужно взять первую производную: .
.
 , заменяя приращения функции ее дифференциалом.
, заменяя приращения функции ее дифференциалом. на микрокалькуляторе, чтобы выяснить, какое число принять за
на микрокалькуляторе, чтобы выяснить, какое число принять за  в точке
в точке  с помощью дифференциала»
с помощью дифференциала» . Вычислим значение функции в точке
. Вычислим значение функции в точке  , или, то же самое:
, или, то же самое: с помощью дифференциала. Вычислим точное значение функции с помощью микрокалькулятора:
с помощью дифференциала. Вычислим точное значение функции с помощью микрокалькулятора: , строго говоря, значение всё равно приближенное, но мы будем считать его точным. Такие уж задачи встречаются.
, строго говоря, значение всё равно приближенное, но мы будем считать его точным. Такие уж задачи встречаются. , получены тысячные доли процента, таким образом, дифференциал обеспечил просто отличное приближение.
, получены тысячные доли процента, таким образом, дифференциал обеспечил просто отличное приближение. , абсолютная погрешность вычислений
, абсолютная погрешность вычислений  , относительная
, относительная . Следующий пример для самостоятельного решения:
. Следующий пример для самостоятельного решения: в
в . Вычислить более точное значение функции в данной точке, оценить абсолютную и относительную погрешность вычислений.
. Вычислить более точное значение функции в данной точке, оценить абсолютную и относительную погрешность вычислений. ; в точке
; в точке .
. , результат округлить до двух знаков после запятой.
, результат округлить до двух знаков после запятой. и т. д.
и т. д. Записываем очевидную функцию
Записываем очевидную функцию 
 нужно представить в виде
нужно представить в виде  . Серьёзную помощь окажет
. Серьёзную помощь окажет  . Таким образом:
. Таким образом:  .
. . По формуле перевода градусов в радианы:
. По формуле перевода градусов в радианы:  (формулы можно найти в той же таблице). Дальнейшее шаблонно:
(формулы можно найти в той же таблице). Дальнейшее шаблонно: .
. (при вычислениях используем значение
(при вычислениях используем значение  ). Результат, как и требовалось по условию, округлён до двух знаков после запятой.
). Результат, как и требовалось по условию, округлён до двух знаков после запятой.
 , результат округлить до трёх знаков после запятой.
, результат округлить до трёх знаков после запятой. . Применительно к рассматриваемому заданию удобнее использовать эквивалентное
. Применительно к рассматриваемому заданию удобнее использовать эквивалентное .
. в точке
в точке  с помощью полного дифференциала, оценить абсолютную и относительную погрешность.
с помощью полного дифференциала, оценить абсолютную и относительную погрешность.  . А вот и рабочая формула:
. А вот и рабочая формула: .
. . Здесь, очевидно:
. Здесь, очевидно: ,
, 
 , что верно при:
, что верно при: ,
,  .
. :
: .
. :
: :
: :
: