Sbor_z_u_m (1)
.pdf
Очевидно, что точка 
должна удовлетворять данному уравнению:
– верное равенство.
Следует отметить, что такая проверка является лишь частичной. Если мы неправильно
вычислили производную в точке 
, то выполненная подстановка нам ничем не поможет. Рассмотрим еще два примера.
Пример 5
Составить уравнение касательной к графику функции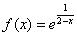 
в точке с абсциссой 
Уравнение касательной составим по формуле
1)Вычислим значение функции в точке 
:
2)Найдем производную. Дважды используем правило дифференцирования сложной функции:
3) Вычислим значение производной в точке |
: |
4) Подставим значения 
, 
и 
в формулу 
:
Готово.
Выполним частичную проверку:
Подставим точку 
в найденное уравнение:
; 
; – верное равенство.
Пример 6
171
Составить уравнение касательной к графику функции 
в точке с абсциссой
Полное решение и образец оформления в конце урока.
В задаче на нахождение уравнения касательной очень важно ВНИМАТЕЛЬНО и аккуратно выполнить вычисления, привести уравнение прямой к общему виду.
Дифференциал функции одной переменной для приближенных вычислений
Коль скоро мы не объяснили (на данный момент) строго, что такое производная функции, то не имеет смысла объяснять, и что такое дифференциал функции. В самой примитивной формулировке дифференциал – это «почти то же самое, что и производная». Точнее – это производная, умноженная на приращение аргумента функции.
Производная функции чаще всего обозначается через 
.
Дифференциал функции стандартно обозначается через 
(так и читается – «дэ игрек») Дифференциал функции одной переменной записывается в следующем виде:
Другой вариант записи: 
Простейшая задача: Найти дифференциал функции 
1)Первый этап. Найдем производную:
2)Второй этап. Запишем дифференциал:
Готово.
Дифференциал функции одной или нескольких переменных чаще всего используют для
приближенных вычислений.
Помимо других задач с дифференциалом время от времени встречается и «чистое» задание на нахождение дифференциала функции. Кроме того, как и для производной, для дифференциала существует понятие дифференциала в точке. И такие примеры мы тоже рассмотрим.
Пример 7
Найти дифференциал функции 
.
Перед тем, как находить производную или дифференциал, всегда целесообразно посмотреть, а нельзя ли как-нибудь упростить функцию (или запись функции) ещё до дифференцирования? Смотрим на наш пример. Во-первых, можно преобразовать корень:
(корень пятой степени относится именно к синусу). Во-вторых, замечаем, что под синусом у нас дробь, которую, очевидно, предстоит дифференцировать. Формула дифференцирования дроби очень громоздка. Нельзя ли
избавиться от дроби? В данном случае – можно, почленно разделим числитель на знаменатель:
172
Функция сложная. В ней два вложения: под степень вложен синус, а под синус вложено
выражение 
. Найдем производную, используя правило дифференцирования сложной функции 
два раза:
Запишем дифференциал, при этом снова представим |
в первоначальном «красивом» |
виде: |
|
Готово.
Когда производная представляет собой дробь, значок 
обычно «прилепляют» в самом конце числителя (можно и справа на уровне дробной черты).
Пример 8
Найти дифференциал функции 
. Это пример для самостоятельного решения.
Следующие два примера на нахождение дифференциала в точке.
Пример 9
Вычислить дифференциал функции 
в точке 
Найдем производную:
Производная вроде бы найдена. Но в это всё предстоит еще подставлять число, поэтому результат максимально упрощаем:
Труды были не напрасны, записываем дифференциал:
173
Теперь вычислим дифференциал в точке 
:
В значок дифференциала 
единицу подставлять не нужно, он немного из другой оперы.
Ну и хорошим тоном в математике считается устранение иррациональности в знаменателе. Для этого домножим числитель и знаменатель на 
. Окончательно:
Пример 10 |
|
|
Вычислить дифференциал функции |
в точке |
. В ходе решения |
производную максимально упростить. |
|
|
Это пример для самостоятельного решения. Примерный образец оформления и ответ в конце урока.
Вторая производная
Всё очень просто. Вторая производная – это производная от первой производной: 
Стандартные обозначения второй производной: 
, 
или 
(дробь читается так: «дэ два игрек по дэ икс квадрат»).
Чаще всего вторую производную обозначают первыми двумя вариантами. Но третий вариант тоже встречается, причем, его очень любят включать в условия контрольных заданий,
например: «Найдите 
функции…». А студент сидит и битый час чешет репу, что это вообще такое, и почему в дроби d не сокращены.
Рассмотрим простейший пример. Найдем вторую производную от функции 
. Для того чтобы найти вторую производную, как многие догадались, нужно сначала найти первую производную:
Теперь находим вторую производную:
Готово.
Рассмотрим более содержательные примеры.
Пример 11
Найти вторую производную функции 
Найдем первую производную:
174
На каждом шаге всегда смотрим, нельзя ли что-нибудь упростить? Сейчас нам предстоит дифференцировать произведение двух функций, и мы избавимся от этой неприятности,
применив известную тригонометрическую формулу 
. Точнее говоря,
использовать формулу будем в обратном направлении: 
:
Находим вторую производную:
Готово.
Можно было пойти другим путём – понизить степень функции еще перед дифференцированием, используя формулу 
:
Если интересно, возьмите первую и вторую производные снова. Результаты, естественно, совпадут.
Отметим, что понижение степени бывает очень выгодно при нахождении частных производных функции. Здесь же оба способа решения будут примерно одинаковой длины и сложности.
Как и для первой производной, можно рассмотреть задачу нахождения второй производной в точке.
Например: Вычислим значение найденной второй производной в точке 
:
Необходимость находить вторую производную и вторую производную в точке возникает при исследовании графика функции на выпуклость/вогнутость и перегибы.
Пример 12
Найти вторую производную функции 
. Найти 
. Это пример для самостоятельного решения.
Аналогично можно найти третью производную, а также производные более высоких порядков. Такие задания встречаются, но значительно реже.
Решения и ответы:
175
Пример 2: Найдем производную:
Вычислим значение функции в точке |
: |
Пример 4: Найдем производную: |
|
Вычислим производную в заданной точке:
Пример 6: Уравнение касательной составим по формуле 
1)Вычислим значение функции в точке 
:
2)Найдем производную. Перед дифференцированием функцию выгодно упростить:
3) Вычислим значение производной в точке |
: |
4) Подставим значения , 
и 
в формулу 
:
176
Пример 8: Преобразуем функцию:
Найдем производную:
Запишем дифференциал:
Пример 10: Найдем производную:
Запишем дифференциал:
Вычислим дифференциал в точке 
: 
.
Пример 12: Найдем первую производную:
Найдем вторую производную:
177
Вычислим: |
. |
7.3. Частные производные. Примеры решений
На данном уроке мы познакомимся с понятием функции двух переменных, а также подробно рассмотрим наиболее распространенное задание – нахождение частных производных первого и второго порядка, полного дифференциала функции.
Для эффективного изучения нижеизложенного материала Вам необходимо уметь более или менее уверенно находить «обычные» производные функции одной переменной. Научиться правильно обращаться с производными можно на уроках Как найти производную? и Производная сложной функции. Также нам потребуется таблица производных элементарных функций и правил дифференцирования, удобнее всего, если она будет под рукой в распечатанном виде.
Начнем с самого понятия функции двух переменных, постараемся ограничиться минимумом теории, так как сайт имеет практическую направленность. Функция двух переменных обычно
записывается как 
, при этом переменные 
, 
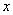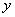называются независимыми переменными или аргументами.
Пример: 
- функция двух переменных.
Иногда используют запись 
. Также встречаются задания, где вместо буквы 
используется буква 
.
Полезно знать геометрический смысл функций. Функции одной переменной 
соответствует определенная линия на плоскости, например, 
– всем знакомая школьная
парабола. Любая функция двух переменных 
с геометрической точки зрения представляет собой поверхность в трехмерном пространстве (плоскости, цилиндры, шары, параболоиды и т.д.). Но, собственно, это уже аналитическая геометрия, а у нас на повестке дня математический анализ.
Переходим к вопросу нахождения частных производных первого и второго порядков. Должен сообщить хорошую новость для тех, кто выпил несколько чашек кофе и настроился на невообразимо трудный материал: частные производные – это почти то же самое, что и
«обычные» производные функции одной переменной.
Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций. Есть только пара небольших отличий, с которыми мы познакомимся прямо сейчас.
Пример 1
Найти частные производные первого и второго порядка функции 
Сначала найдем частные производные первого порядка. Их две.
178
Обозначения:
или 
– частная производная по «икс»
или 
– частная производная по «игрек»
Начнем с 
.
Важно! Когда мы находим частную производную по «икс», то переменная 
считается
константой (постоянным числом).
Решаем. На данном уроке будем сразу приводить полное решение, а комментарии давать ниже.
Комментарии к выполненным действиям:
(1) Первое, что мы делаем при нахождении частной производной – заключаем всю функцию в скобки под штрих с подстрочным индексом.
Внимание, важно! Подстрочные индексы НЕ ТЕРЯЕМ по ходу решения. В данном случае,
если Вы где-нибудь нарисуете «штрих» без 
, то преподаватель, как минимум, может поставить рядом с заданием 
(сразу откусить часть балла за невнимательность).
Далее данный шаг комментироваться не будет, все сделанные замечания справедливы для любого примера по рассматриваемой теме.
(2) Используем правила дифференцирования 
; 
. Для простого примера, как этот, оба правила вполне можно применить на одном шаге. Обратите внимание на первое слагаемое: так как 
считается константой, а любую константу можно вынести за
знак производной, то 
мы выносим за скобки. То есть в данной ситуации 
ничем не лучше обычного числа. Теперь посмотрим на третье слагаемое 
: здесь, наоборот, выносить
нечего. Так как 
константа, то 
– тоже константа, и в этом смысле она ничем не лучше последнего слагаемого – «семерки».
(3)Используем табличные производные 
и 
.
(4)Упрощаем ответ.
Теперь определим 
. Когда мы находим частную производную по «игрек», то переменная
считается константой (постоянным числом).
(1) Используем те же правила дифференцирования |
; |
. В первом |
слагаемом выносим константу 
за знак производной, во втором слагаемом ничего вынести
нельзя поскольку 
– уже константа.
(2) Используем таблицу производных элементарных функций. Мысленно поменяем в таблице
все «иксы» на «игреки». То есть данная таблица рАвно справедлива для 
(и вообще для любой буквы). В данном случае, используемые нами формулы имеют вид: 
и
.
Итак, частные производные первого порядка найдены
179
Особенности вычисления частных производных
Подведем итог, чем же отличается нахождение частных производных от нахождения «обычных» производных функции одной переменной:
1)Когда мы находим частную производную 
, то переменная 
считается константой.
2)Когда мы находим частную производную 
, то переменная 
считается константой.
3)Правила и таблица производных элементарных функций справедливы и
применимы для любой переменной (
, 
либо какой-нибудь другой), по которой ведется дифференцирование.
Шаг второй. Находим частные производные второго порядка. Их четыре.
Обозначения:
или 
– вторая производная по «икс»
или 
– вторая производная по «игрек»
или 
– смешанная производная «по икс игрек»
или 
– смешанная производная «по игрек икс» В понятии второй производной нет ничего сложного. Говоря простым языком, вторая
производная – это производная от первой производной.
Для наглядности я перепишу уже найденные частные производные первого порядка:
Сначала найдем смешанные производные:
Как видите, всё просто: берем частную производную |
и дифференцируем ее еще раз, но в |
данном случае – уже по «игрек». |
|
Аналогично: |
|
Для практических примеров, когда все частные производные непрерывны, справедливо следующее равенство:
Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.
Находим вторую производную по «икс».
Никаких изобретений, берем 
и дифференцируем её по «икс» еще раз:
Аналогично:
Следует отметить, что при нахождении , нужно проявить повышенное внимание, так как никаких чудесных равенств для проверки не существует.
180