Содержание тестовых материалов Линейная алгебра и элементы аналитической геометрии Векторные пространства
1. Задание {{ 71 }} ТЗ № 120
Даны векторы а=(3; 5), b=(2; -7). Линейная комбинация векторов 4a-0,5b равна:
(11; 23,5)
(11; 8,5)
(20; 1)
(4; -1)
2. Задание {{ 72 }} ТЗ № 121
Даны векторы а=(-2; 4), b=(3; 1). Линейная комбинация векторов 3a+5b равна:
(-3; 13)
(9; 17)
(21; 17)
(-9; -17)
3. Задание {{ 73 }} ТЗ № 122
Линейной операцией над векторами называется:
определение координат векторов
определение длины векторов
определение направления векторов
сложение векторов
умножение векторов на действительное число
4. Задание {{ 74 }} ТЗ № 123
При умножении вектора а на действительное число λ получают:
вектор, коллинеарный вектору а
вектор, ортогональный вектору а
вектор, сонаправленный вектору а
вектор, противоположно направленный вектору а;
скаляр
ничего сказать нельзя
5. Задание {{ 75 }} ТЗ № 124
Размерность n-мерного векторного пространства определяется
числом векторов, входящих в n-мерное пространство
числом компонент, характеризующих вектор
числом координат вектора
длиной вектора
6. Задание {{ 76 }} ТЗ № 125
Линейной комбинацией векторов а1; а2 ;…; аn n-мерного векторного пространства является выражение:
λi ai
7. Задание {{ 77 }} ТЗ № 172
Скалярное произведение векторов в n-мерном пространстве определяется:
(a,b) = |a| * |b| * cosφ
(a,b)
(a,b)
(a,b)
8. Задание {{ 239 }} ТЗ № 239
Имеется система векторов на плоскости, в которую включён нулевой вектор. Эта система векторов является:
линейно независимой
линейно зависимой
ортогональной
ничего сказать нельзя
9. Задание {{ 240 }} ТЗ № 240
Какие
три из четырёх векторов
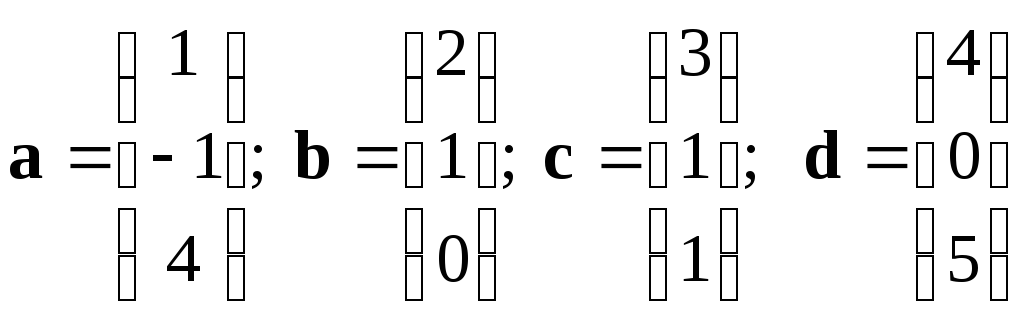не образуют базис в пространстве?
a, b, c
b, c, a
a, c, d
b, c, d
Векторы на плоскости и в пространстве
10. Задание {{ 44 }} ТЗ № 207
Даны
два векторы:
,
причём известно, что
;
Эти векторы:
сонаправлены
противоположно направлены
ортогональны
коллинеарны
о векторах ничего сказать нельзя
11. Задание {{ 45 }} ТЗ № 208
Даны два вектора: а = (-1; 2; 5) и b = (3; 0; 5). Скалярное произведение векторов равно:
22
15
-2
0
12. Задание {{ 46 }} ТЗ № 209
Даны два вектора: а = (-2; 2; 5) и b = (3; 0; 5). Скалярное произведение векторов равно:
32
19
-2
10
13. Задание {{ 47 }} ТЗ № 210
Даны
векторы:
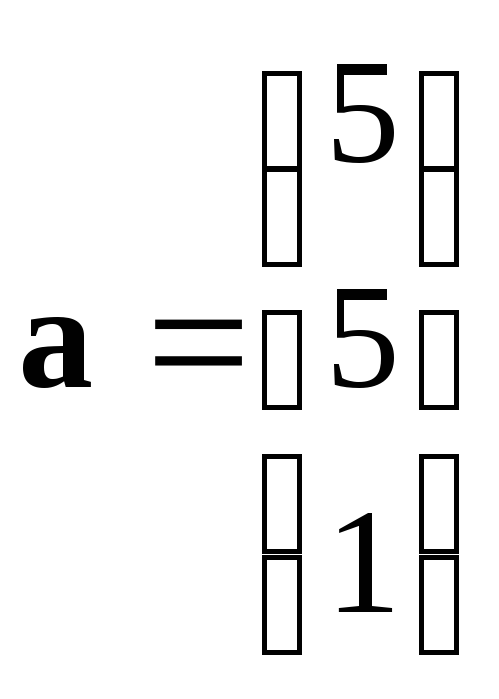и
.
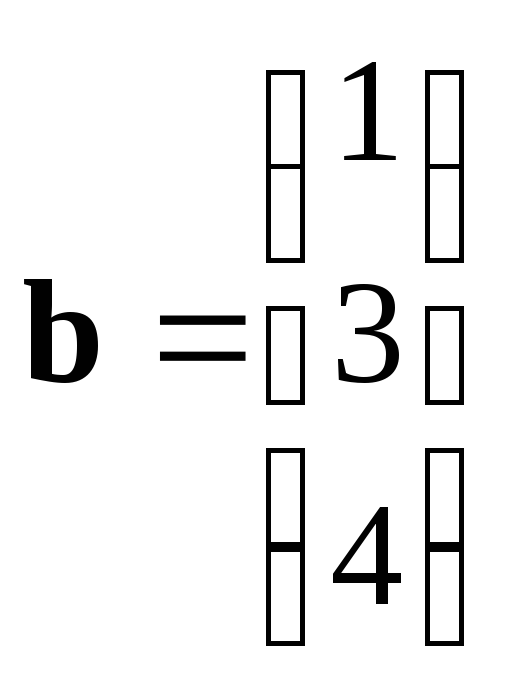Косинус угла между этими векторами
равен:
0.6591
0.7011
0.8851
-0.6233
14. Задание {{ 48 }} ТЗ № 211
Даны
векторы:
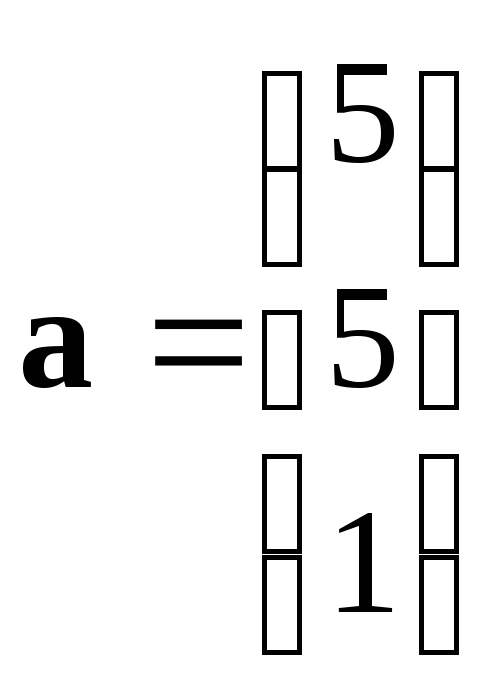и
.
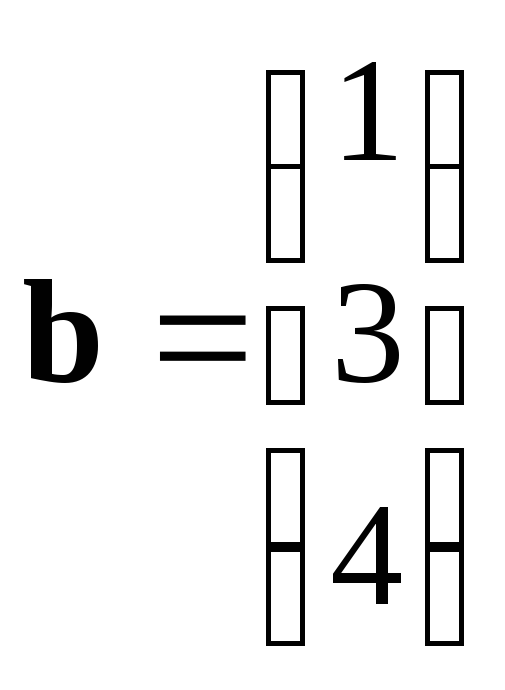Угол между векторами:
острый
тупой
прямой
нулевой
15. Задание {{ 49 }} ТЗ № 212
Даны
векторы:
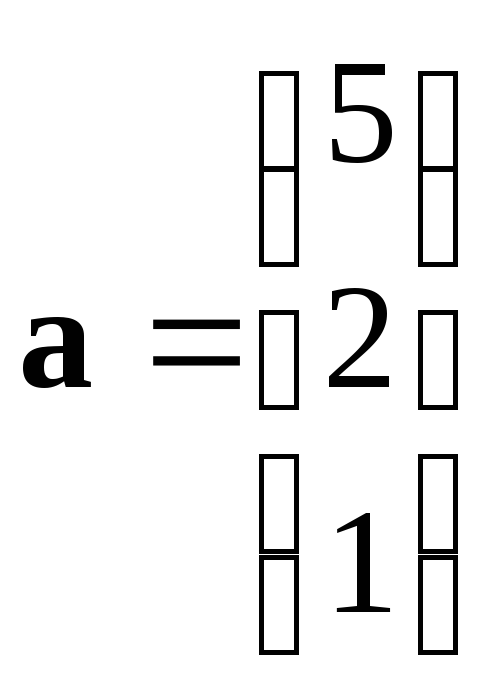и
.
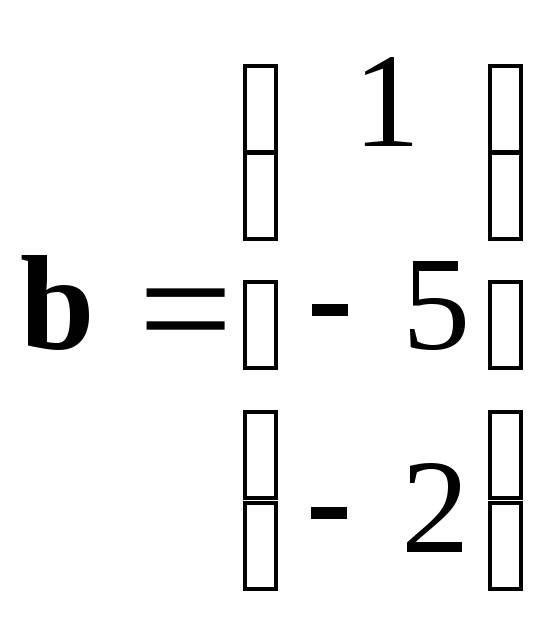Угол между векторами:
острый
тупой
прямой
нулевой
16. Задание {{ 50 }} ТЗ № 213
Даны
векторы:
и
.
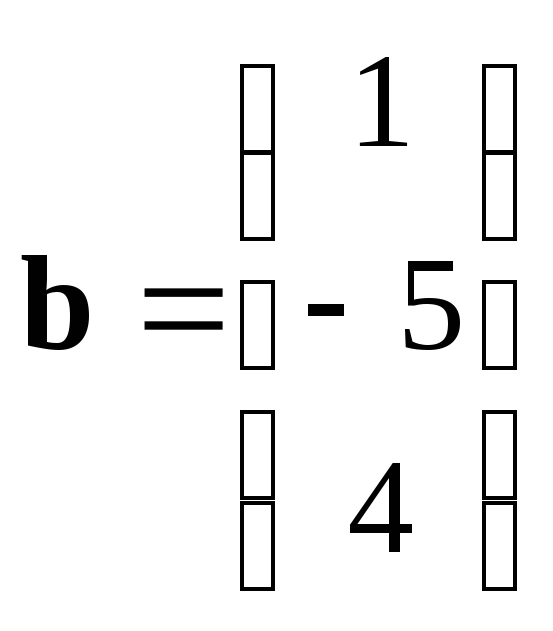Угол между векторами:
острый
тупой
прямой
нулевой
17. Задание {{ 51 }} ТЗ № 214
Орт вектора а = (6; 2; -1) имеет координаты:
18. Задание {{ 52 }} ТЗ № 215
Вектор
а = (6; 2; -1) образует с осью
:
острый угол
тупой угол
прямой угол
нулевой угол
19. Задание {{ 53 }} ТЗ № 216
Вектор
а = (6; 2; -1) образует с осью
:
острый угол
тупой угол
прямой угол
нулевой угол
20. Задание {{ 54 }} ТЗ № 217
Вектор
а = (6; 2; -1) образует с осью
:
острый угол
тупой угол
прямой угол
нулевой угол
21. Задание {{ 55 }} ТЗ № 218
Направляющий
косинус угла, который образует вектор
а = (6; 2; -1) с осью
,
равен:
–1,15
1,05
22. Задание {{ 56 }} ТЗ № 219
Направляющий
косинус угла, который образует вектор
а = (6; 2; -1) с осью
,
равен:
–0,15
0,05
23. Задание {{ 57 }} ТЗ № 220
Направляющий
косинус угла, который образует вектор
а = (6; 2; -1) с осью
,
равен:
–0,15
0,05
24. Задание {{ 58 }} ТЗ № 221
Векторы
а = (-1; 2; 3) и b
= (k;
-10; 4) коллинеарны при значении постоянной
,
равному:
–3
12
5
ни при каком
25. Задание {{ 59 }} ТЗ № 222
Векторы
а = (1; 2; 1) и b
= (k;
8; -4) коллинеарны при значении постоянной
,
равному:
4
12
5
ни при каком
26. Задание {{ 60 }} ТЗ № 223
Векторы
а = (1; 2; 1) и b
= (k;
-8; -4) ортогональны при значении постоянной
,
равному:
-4
12
20
5
ни при каком
27. Задание {{ 61 }} ТЗ № 224
Векторы
а = (1; 2; 1) и b
= (k;
-8; -4) коллинеарны при значении постоянной
,
равному:
-12
12
20
5
ни при каком
28. Задание {{ 62 }} ТЗ № 225
Даны два вектора: а = (-2; 4; -2) и b = (0; 2; 4). Эти векторы:
коллинеарны и противоположно направлены
ортогональны
сонаправлены
ничего сказать нельзя
29. Задание {{ 63 }} ТЗ № 226
Даны два вектора: а = (2; -1; 1) и b = (1; -2; 3). Координаты векторного произведения:
(-1; -5; -1)
(2; 12; 0)
(-5; 0; 4)
(0; 0; 0)
30. Задание {{ 64 }} ТЗ № 227
Даны два вектора: а = (0; 3; 0) и b = (3; -2; 1). Координаты векторного произведения:
(-1; -5; -1)
(3; 0; -9)
(-1;0; 7)
(0; 7; 0)
31. Задание {{ 65 }} ТЗ № 228
Даны два вектора: а = (1; 3; 0) и b = (3; -2; 1). Координаты векторного произведения:
(-3; 1;-11)
(3; 0; -9)
(-1; 0; 7)
(0; 7; 0)
32. Задание {{ 66 }} ТЗ № 229
Даны два вектора: а = (-4; 0; 5) и b = (3; 1; -5). Скалярное произведение векторов равно:
22
19
-37
10
33. Задание {{ 67 }} ТЗ № 230
Даны два вектора: а = (1; 4; -3) и b = (1; 1; -5). Скалярное произведение векторов равно:
20
19
-37
10
34. Задание {{ 68 }} ТЗ № 231
Даны
два вектора: а = (-4; 2; 1) и b
= (-5; 2; 4). Векторное произведение
:
с = (-3; 0; 22)
с = (-5; 7; 2)
с = (-15; 17; 2)
с = (6; 21; 2)
35. Задание {{ 69 }} ТЗ № 232
Даны в пространстве три вектора: а = (1; -3; 5); b = (2; -1; 1); с = (3; -4; 6). Эти векторы:
коллинеарны
ортогональны
компланарны
не лежат в одной плоскости
36. Задание {{ 70 }} ТЗ № 233
Даны два вектора: а = (-3; 2; 4) и b = (4; 2; 0). Угол между этими векторами:
острый
тупой
прямой
нулевой
37. Задание {{ 78 }} ТЗ № 13
Даны точки А(4; -1), В(-3; -2), С(-2; 5). Координаты векторов ВА и ВС равны:
ВА=(7; 1) ВС=(1; 7)
ВА=(1; 7) ВС=(7; 1)
ВА=(-12; 2) ВС=(6; -10)
ВА=(-7; -1) ВС=(-1; -7)
38. Задание {{ 79 }} ТЗ № 14
Даны точки А(3; 2), В(-1; 5), С(0; 3). Координаты векторов АВ и ВС равны:
АВ=(-4; 3) ВС=(1; -2)
АВ=(4; -3) ВС=(-1; 2)
АВ=(2; 7) ВС=(-1; 8)
АВ=(-4; 3) ВС=(-1; 2)
39. Задание {{ 80 }} ТЗ № 15
Даны точки А(2; 3), В(-1; -3), С(-7; 5). Координаты векторов АВ и СВ равны:
АВ=(1; 0) СВ=(-8; 2)
АВ=(-3; -6) СВ=(6; -8)
АВ=(-2; 9) СВ=(7; -15)
АВ=(3; 6) СВ=(-6; 8)
40. Задание {{ 81 }} ТЗ № 16
Даны точки А(4; 0), В(-1; 3), С(5; 7). Координаты векторов АВ и АС равны:
АВ =(-5; 3) АС =(1; 7)
АВ =(3; 3) АС =(9; 7)
АВ =(-4; 0) АС =(20; 0)
АВ =(5; -3) АС =(-1; -7)
41. Задание {{ 82 }} ТЗ № 17
Даны точки А(3; -1), В(0; -5), С(-2; 1). Координаты векторов АВ и ВС равны:
АВ =(3; 4) АС =(2; -6)
АВ =(-3; -4) АС =(-2; 6)
АВ =(3; 6) АС =(-2; 4)
АВ =(1; 0) АС =(-2; 6)
42. Задание {{ 83 }} ТЗ № 18
Определить координаты точки А, с которой совпадает конец вектора а=(3; -1; 4), если его начало совпадает сточкой В(1; 2 -3)
(2; -3; 7)
(4; 1; 1)
(-2; 3; -7)
(3; -2; -12)
(6; 20)
43. Задание {{ 84 }} ТЗ № 19
Даны векторы а=(1; -3; -2), b=(3; 6; -1), сумма векторов равна:
(4; 3; 3)
(-4; 8)
(4; 3; -3)
(4; 9; 3)
44. Задание {{ 85 }} ТЗ № 20
Даны векторы а=(5; 3; -2), b=(-1; 0; -1), разность векторов а и b равна:
(6; 2)
(4; 3; -3)
(-6; -3; 1)
(6; 3; -1)
45. Задание {{ 86 }} ТЗ № 22
Известны модули векторов |a|=13, |b|=19, |a+b|=24. Модуль вектора |a-b| равен:
24
22
32
6
46. Задание {{ 87 }} ТЗ № 23
Даны точки А(3; -1), В(0; -5), С(-2; 1). Сумма векторов АВ+ВС равна:
(-5; 2)
(1; -10)
(5; -2)
(-5; 0)
47. Задание {{ 88 }} ТЗ № 24
Даны точки А(3; -1), В(0; -5), С(-2; 1). Разность векторов АВ-ВС равна:
(-1; -10)
(1; -2)
(1; 10)
(-1; -12)
48. Задание {{ 89 }} ТЗ № 25
Даны точки А(3; -1), В(0; -5), С(-2; 1). Вектор 2АВ-3ВС равен:
(12; -24)
(0; -26)
(0; -10)
(0; -30)
49. Задание {{ 90 }} ТЗ № 26
Даны точки А(4; 0), В(-1; 3), С(5; 7). Сумма векторов АВ+АС равна:
(12; 10)
(16; 0)
(-4; 10)
(4; -10)
50. Задание {{ 91 }} ТЗ № 27
Даны точки А(4; 0), В(-1; 3), С(5; 7). Разность векторов АВ-АС равна:
(6; 4)
(-24; 0)
(4; -10)
(-6; -4)
51. Задание {{ 92 }} ТЗ № 28
Даны точки А(4; 0), В(-1; 3), С(5; 7). Вектор 5АС-3АВ равен:
(-10; 26)
(36; 26)
(88; 0)
(-20; 36)
52. Задание {{ 93 }} ТЗ № 29
Даны точки А(3; 5; 7), В(-1; 4; 2), С(0; -3; 5). Сумма векторов АВ+ВС равна:
(3; 8; 2)
(-3; -8; -2)
(2; 6; 14)
(15; 6; 2)
53. Задание {{ 94 }} ТЗ № 30
Даны точки А(3; 5; 7), В(-1; 4; 2), С(0; -3; 5), D(6; -7; 8). Вектор 2АВ-3СD равен:
(26; -10; 18)
(-12; 12; -21)
(40; -18)
(-26; 10; -19)
54. Задание {{ 95 }} ТЗ № 31
Длина вектора а=(5; 12) равна:
13
-13
-
55. Задание {{ 96 }} ТЗ № 32
Длина вектора а=(7; -1) равна:
2
5
-5
4
56. Задание {{ 97 }} ТЗ № 33
Длина
вектора а=(5; 2
)
равна:
1
7
-7
57. Задание {{ 98 }} ТЗ № 34
Длина вектора а=(5; 7) равна:
-
58. Задание {{ 99 }} ТЗ № 35
Длина вектора а=(-6; 8) равна:
10
34
-10
59. Задание {{ 100 }} ТЗ № 36
Длина вектора а=(7; -7) равна:
14
-
7
60. Задание {{ 101 }} ТЗ № 37
Длина
вектора а=(5;
-3;
)
равна:
2
-6
6
36
61. Задание {{ 102 }} ТЗ № 38
Длина вектора а=(-2; 3; 1) равна:
-
14
6
62. Задание {{ 103 }} ТЗ № 39
Длина вектора а=(0; 12; 5) равна:
13
-13
17
63. Задание {{ 104 }} ТЗ № 40
Длина вектора а=(-5; 7; 2) равна:
-
14
64. Задание {{ 105 }} ТЗ № 41
Длина вектора a = 2i +3j - 6k равна:
-1
-7
7
11
65. Задание {{ 106 }} ТЗ № 42
Известны
модули векторов |a|
= 2, |b|
= 3, угол между
векторами φ=
.
Длина вектора с = 3а - 4b равна:
6
-6
-6
6
66. Задание {{ 107 }} ТЗ № 43
Известны модули векторов |a| = 2, |b| =3 и угол между ними φ=60°.
Длина вектора с = 2а - b равна:
2
-2
2
1
67. Задание {{ 108 }} ТЗ № 44
Даны вектора а=(3; -5; 8), b=(-1; 1; -4). Модуль суммы векторов равен:
(2; -4; 4)
6
-6
-40
68. Задание {{ 109 }} ТЗ № 45
Даны вектора а=(3; -5; 8), b=(-1; 1; -4). Модуль разности векторов равен:
(4; -6; 12)
-14
14
-40
69. Задание {{ 110 }} ТЗ № 46
Даны точки А(5; 2), В(8; -2), длина вектора АВ равна:
5
-5
1
7
70. Задание {{ 111 }} ТЗ № 47
Даны точки А(3; 5), В(-3; 3), длина вектора АВ равна:
2
40
-
71. Задание {{ 112 }} ТЗ № 48
Даны точки А(7; 7), В(4; 3), длина вектора АВ равна:
-5
25
5
-7
72. Задание {{ 113 }} ТЗ № 49
Вектор задан своими координатами А(5; 3; 1), В(4; 5; 1), длина вектора равна:
-
1
19
73. Задание {{ 114 }} ТЗ № 50
Вектор задан своими координатами А(3; -2; -5), В(7; 6; -1), длина вектора равна:
4
-4
16
14
74. Задание {{ 115 }} ТЗ № 51
Дан треугольник с вершинами А(3; -2; 8), В(-1; 0; 6), С(5; 1; -7), длина стороны АВ равна:
14
42
75. Задание {{ 116 }} ТЗ № 52
Дан треугольник с вершинами А(-1; -2; 4), В(-4; -2; 0), С(3; -2; 1), длина стороны АВ равна:
5
(-3; 0; -4)
5
-5
76. Задание {{ 117 }} ТЗ № 53
Дан треугольник с вершинами А(-1; -2; 4), В(-4; -2; 0), С(3; -2; 1), длина стороны ВС равна:
-5
(7; 0; 1)
5
5
77. Задание {{ 118 }} ТЗ № 54
Даны точки А(1; 3), В(-3; 0). Расстояние между точками А и В равно:
5
(-4; -3)
-5
(-2; 3)
78. Задание {{ 119 }} ТЗ № 55
Даны точки А(1; 3), В(5; 0). Расстояние между точками А и В равно:
(4; -3)
5
-5
(6; 3)
79. Задание {{ 120 }} ТЗ № 56
Даны точки А(12; 14), В(0; 19). Расстояние между точками А и В равно:
-13
(-12; 5)
13
-7
80. Задание {{ 121 }} ТЗ № 57
Даны точки А(12; 14), В(0; 9). Расстояние между точками А и В равно:
-17
(-12; -5)
13
-13
81. Задание {{ 122 }} ТЗ № 58
Даны точки А(8; 6), В(0; 0). Расстояние между точками А и В равно:
10
-10
(-8; -6)
14
82. Задание {{ 123 }} ТЗ № 59
На оси абсцисс находится точка М, расстояние от которой до точки А(3; -3) равно 5. Координаты точки М:
(-1; 0)
(7; 0)
(8; 0)
(8; 2)
83. Задание {{ 124 }} ТЗ № 60
Точка К делит отрезок MN в отношении |MK|:|KN|=2:3, координаты точки М(7; 4) и точки N(-3; 9). Точка К имеет следующие координаты:
(3; 6)
(1,8; 6)
84. Задание {{ 125 }} ТЗ № 61
Точка К делит отрезок MN в отношении |MK|:|KN|=1:2, координаты точки М(5; 1) и точки N(-4; -14). Точка К имеет следующие координаты:
(2; -4)
85. Задание {{ 126 }} ТЗ № 62
Точка К делит отрезок MN в отношении |MK|:|KN|=2:1, координаты точки М(5; 1) и точки N(-4; -14). Точка К имеет следующие координаты:
(0,5; -6,5)
(-1; -9)
(1; 9)
86. Задание {{ 127 }} ТЗ № 63
Отрезок АВ задан точками А(2; 3), В(10; 11), точка С делит отрезок в отношении 3:5. Точка С имеет следующие координаты:
(6; 5)
(7; 11)
(5; 6)
87. Задание {{ 128 }} ТЗ № 64
Отрезок АВ задан точками А(-5; -1), В(4; 2,5), точка С делит отрезок в отношении 5:2. Точка С имеет следующие координаты:
(-2; 3)
(3; -2)
(-2; 0)
88. Задание {{ 129 }} ТЗ № 65
Началом отрезка служит точка А(-3; -5), а серединой - точка С(3; -2). Конец отрезка - точка В - имеет координаты:
(2; 4)
(3; 2)
(4; 2)
(4; 6)
89. Задание {{ 130 }} ТЗ № 66
Середина отрезка, заданного точками А(-12; -1), В(-1; 8), имеет координаты:
(3,5; -6,5)
(6,5; 3,5)
(-5,5; 4,5)
(-6,5; 3,5)
90. Задание {{ 131 }} ТЗ № 67
Середина отрезка, заданного точками А(6; -12), В(12, -6), имеет координаты:
(9; -9)
(-9; 9)
(10; -8)
(3; -3)
91. Задание {{ 132 }} ТЗ № 68
Середина отрезка, заданного точками А(3; -7; 11), В(-1; 3, -3), имеет координаты:
(2; 5; 7)
(1; -2; 4)
(3,5; -0,5)
92. Задание {{ 133 }} ТЗ № 69
Дан равносторонний треугольник АВС со стороной, равной 6, скалярное произведение векторов АВ и АС равно:
18
-18
36
12
93. Задание {{ 134 }} ТЗ № 70
Дан равносторонний треугольник АВС со стороной, равной 6, скалярное произведение векторов АВ и ВС равно:
18
-18
36
12
94. Задание {{ 135 }} ТЗ № 71
Дан треугольник АВС – прямоугольный и равнобедренный, < С=90°, катеты равны 5. Скалярное произведение векторов АС и АВ равно:
5
25
5
-25
95. Задание {{ 136 }} ТЗ № 72
Дан треугольник АВС – прямоугольный и равнобедренный, < С=90°, катеты равны 5. Скалярное произведение векторов СА и СВ равно:
5
5
25
0
96. Задание {{ 137 }} ТЗ № 73
Началом отрезка служит точка А(-3; -5), а серединой - точка С(3; -2). Конец отрезка - точка В - имеет координаты:
(1; 9)
(9; 1)
(15; 4)
(0; -7)
97. Задание {{ 138 }} ТЗ № 75
Заданы векторы, такие, что |a|=2, |b|=7, а угол φ между ними 30°. Скалярное произведение векторов (3а+b)(а+3b) равно:
159+70
195,5
299
98. Задание {{ 139 }} ТЗ № 76
Заданы векторы, такие, что |a|=3, |b|=4, а угол φ между ними 60°. Квадрат суммы векторов (а+b)2 равен:
49
25+12
37
12,25
99. Задание {{ 140 }} ТЗ № 77
Заданы векторы, такие, что |a|=3, |b|=4, а угол φ между ними 60°. Скалярное произведение векторов (3а-5b)∙2а равно:
66
-66
6
-6
100. Задание {{ 141 }} ТЗ № 78
Скалярное произведение векторов а=(5; 7), b=(4; 3) равно:
41
47
101. Задание {{ 142 }} ТЗ № 79
Скалярное произведение векторов а=(-3; 5), b=(16; 1) равно:
1
-43
43
136
102. Задание {{ 143 }} ТЗ № 80
Скалярное произведение векторов а=(2; 0), b=(-3; -7) равно:
21
6
-6
-20
103. Задание {{ 144 }} ТЗ № 81
Скалярное произведение векторов а=(-3; 1), b=(1; -3) равно:
4
-4
6
-6
104. Задание {{ 145 }} ТЗ № 82
Скалярное произведение векторов а=(5; -7), b=(7; 5) равно:
0
70
10
24
105. Задание {{ 146 }} ТЗ № 83
Скалярное произведение векторов а=(2; 0), b=(0; -3) равно:
-6
0
-1
6
106. Задание {{ 147 }} ТЗ № 84
Скалярное произведение векторов a = 3i +4j + 7k , b = 2i - 3j + 2k равно:
(6, -12, 9)
21
8
-19
107. Задание {{ 148 }} ТЗ № 85
Угол между векторами а=(4; 0), b=(2; -2) равен:
30°
-30°
108. Задание {{ 149 }} ТЗ № 86
Даны точки на плоскости А(1; 6), В(1; 0), С(-2; 3), угол между векторами АВ и ВС равен:
135°
-45°
109. Задание {{ 150 }} ТЗ № 87
Угол между векторами а=(6; -2), b=(9; -12) равен:
0,8222
arccos 0,8222
110. Задание {{ 151 }} ТЗ № 88
Угол между векторами а=(-2; 3), b=(4; -1) равен:
arccos 0,7399
0,7399
arccos 0,7778
0,7778
111. Задание {{ 152 }} ТЗ № 89
Вектора образуют угол φ=60°, причем |a|=3, |b|=8. Модуль суммы векторов |a+b| равен:
-
11
5,5
112. Задание {{ 153 }} ТЗ № 90
Вектора образуют угол φ=60°, причем |a|=3, |b|=8. Модуль разности векторов |a-b| равен:
2,5
5
7
-7
113. Задание {{ 154 }} ТЗ № 91
Угол между векторами a = i + 2j + 3k , b = 6i + 4j - 2k равен:
45°
114. Задание {{ 155 }} ТЗ № 92
Даны точки А(2; 0; 0), В(0; 0; 4), С(2; 0; 2), О(0; 0; 0). Угол между векторами ОС и АВ равен:
115. Задание {{ 156 }} ТЗ № 93
Дан треугольник с вершинами А(-1; -2; 4), В(-4; -2; 0), С(3; -2; 1), угол А равен:
90°
45°
116. Задание {{ 157 }} ТЗ № 94
Дан треугольник с вершинами А(-1; -2; 4), В(-4; -2; 0), С(3; -2; 1), угол В равен:
90°
45°
117. Задание {{ 158 }} ТЗ № 95
Дан треугольник с вершинами А(-1; -2; 4), В(-4; -2; 0), С(3; -2; 1), угол С равен:
90°
45°
118. Задание {{ 159 }} ТЗ № 96
Векторы а = -2i + 3j + βk , b = αi - 6j + 2k коллинеарные, если α и β соответственно равны:
α = 4 β = -1
α = 1 β = -4
α = -2 β = 2
α = -1 β = 4
119. Задание {{ 160 }} ТЗ № 97
Векторы а = mi - 3j + 2k , b = i +2j – mk ортогональны, если m равно:
6
-6
0
-1
120. Задание {{ 161 }} ТЗ № 98
Вектор b, коллинеарный вектору а=(2; 1; -1), имеет координаты:
(5; 4; 2)
(6; -3; -3)
(3; 1,5; -1,5)
(8; 4; 4)
121. Задание {{ 162 }} ТЗ № 99
Векторы а = i +2 j + βk , b = αi - 4j - 2k коллинеарные, если α и β соответственно равны:
α = -2 β = 1
α = 1 β = -2
α = 2 β = -1
α = -1 β = -2
122. Задание {{ 163 }} ТЗ № 100
Векторы а = 2i – mj + 4k , b = mi + 5j - 6k ортогональны, если m равно:
8
-8
1
0
123. Задание {{ 164 }} ТЗ № 101
Векторы а = 4i + 2j – mk , b = 3i – mj + 4k ортогональны, если m равно:
2
-2
1
0
124. Задание {{ 165 }} ТЗ № 102
Вектор b, ортогональный вектору а=(2; -4; 1), имеет координаты:
(5; 4; 2)
(6; -3; -3)
(3; 2; 2)
(8; 4; 4)
125. Задание {{ 166 }} ТЗ № 103
Вектор b, ортогональный вектору а=(3; -2; -4), имеет координаты:
(-4; -8; 1)
(1; 2; 3)
(5; 1; 0)
(2; -4; 5)
126. Задание {{ 167 }} ТЗ № 104
Вектор b, ортогональный вектору а=(-4; 4; -8), имеет координаты:
(1; -3; -2)
(2; 4; -1)
(5; 3; 0)
(-4; 8; -8)
127. Задание {{ 168 }} ТЗ № 105
Векторы а = 5i – mj + 8k , b = -6i + 7j – mk ортогональны, если m равно:
2
-2
0
-1
128. Задание {{ 169 }} ТЗ № 106
Векторы а = i + αj - 5k; b = -4i + 16j - βk коллинеарные, если α и β соответственно равны:
α = -4 β = 20
α = 4 β = -20
α = -4 β = -20
α = 4 β = 20
129. Задание {{ 170 }} ТЗ № 107
Вектор b, коллинеарный вектору а=(3; -2; 5), имеет координаты:
(-3; 2; -5)
(1,5; -1; 2,5)
(6; 4; 10)
(6; 4; -10)
130. Задание {{ 171 }} ТЗ № 108
Вектором называется:
направленный отрезок
отрезок с координатами начала и конца
символ, обозначенный латинскими буквами со стрелкой наверху
отрезок, имеющий проекции на координатные оси
131. Задание {{ 172 }} ТЗ № 109
Вектор, начало и конец которого совпадают, называется:
нормой вектора
ортом вектора
единичным вектором
нулевым вектором
132. Задание {{ 173 }} ТЗ № 110
Векторы называются равными:
если они ортогональны и имеют одинаковые длины
если они коллинеарные и сонаправленые и имеют одинаковые длины
если их соответствующие координаты пропорциональны
если их модули равны
133. Задание {{ 174 }} ТЗ № 111
Модуль вектора определяется:
как, корень квадратный из суммы квадратов его компонентов
латинским символом |a|
по теореме Пифагора
скалярной величиной
134. Задание {{ 175 }} ТЗ № 112
Ортом вектора называется:
тройка векторов i, j, k
единичный вектор, имеющий с данным вектором одинаковое направление
вектор, модуль которого равен единицы
вектор, начало которого совпадает с началом декартовой системы координат
135. Задание {{ 176 }} ТЗ № 113
Можно ли назвать компоненты вектора
его координатами
его проекциями на координатные оси
его ортами
его базисом
136. Задание {{ 177 }} ТЗ № 114
В понятии "направляющий косинус" имеется в виду угол:
между двумя векторами в определении их скалярного произведения
между двумя векторами в определении их векторного произведения
между вектором и осью координат
между вектором и его проекцией на ось
137. Задание {{ 178 }} ТЗ № 115
Выражение cos2α + cos2β + cos2γ = 1 справедливо
для всех векторов 3-х мерного пространства
только для единичных векторов
только для коллинеарных векторов
только для ортогональных векторов
ничего сказать нельзя
138. Задание {{ 179 }} ТЗ № 116
С помощью правила треугольника или параллелограмма определяется:
модуль векторов
сумма векторов
разность векторов
умножение вектора на действительное число
скалярное произведение векторов
векторное произведение векторов
139. Задание {{ 180 }} ТЗ № 117
Два вектора, имеющие пропорциональные соответствующие координаты:
сонаправленые
противоположно направлены
коллинеарные
ортогональные
ничего сказать нельзя
140. Задание {{ 181 }} ТЗ № 168
Скалярное произведение векторов в 2-х мерном пространстве определяется:
(a,b) = |a| * |b| * sinφ
(a,b) = |a| * |b| * cosφ
(a,b)
(a,b) = ax bx + ay by
141. Задание {{ 182 }} ТЗ № 169
Скалярное произведение векторов в 3-х мерном пространстве определяется:
(a,b) = |a| * |b| * sinφ
(a,b) = |a| * |b| * cosφ
(a,b)
(a,b) = ax bx + ay by + az bz
142. Задание {{ 183 }} ТЗ № 170
Какое из перечисленных выражений не относится к свойствам скалярного произведения:
(a * b) = (b * а)
(а, b + c) = (a * b) + (b * c)
(a * λb) = (λa, b) = λ (a, b)
(a * b) = |a| * |b| * cosφ
143. Задание {{ 184 }} ТЗ № 171
Какие из перечисленных выражений справедливы для тройки векторов i, j, k:
(i * j) = (i * k) = (j * k) = 0
(i * j) = (i * k) = (j * k) = 1
(i * i) = (j * j) = (k * k) = 0
(i * i) = (j * j) = (k * k) = 1
144. Задание {{ 185 }} ТЗ № 173
В понятии "направляющий косинус" имеется в виду угол:
между двумя векторами в определении их векторного произведения
между вектором и осью координат
между вектором и его проекцией на ось
между двумя векторами в определении их скалярного произведения
145. Задание {{ 186 }} ТЗ № 174
Известны модули векторов |a|=11, |b|=23, |a-b|=30. Модуль вектора |a+b| равен:
20
34
5
30
146. Задание {{ 187 }} ТЗ № 206
Заданы два вектора, такие, что |a|=5, |b|=3, а угол между ними 45°. Квадрат суммы векторов (а+b)2 равен:
34+15
64
32
17