
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра САПР
Курсовая РАБОТА
по дисциплине «Схемотехника»
Тема: Дискретное косинусное преобразование
Студент гр. 8363 |
|
Нерсисян А.С. |
Преподаватель |
|
Фахми Ш.С. |
Санкт-Петербург
2020
ЗАДАНИЕ
на курсовую работу
Студент Нерсисян А.С. |
||
Группа 8363 |
||
Тема работы: Дискретное косинусное преобразование Исходные данные: Продемонстрировать рабочий вариант реализации дискретного косинусного преобразования изображения. Содержание пояснительной записки: Аннотация, содержание, введение, теоретическая часть, препроцессинг, дискретное косинусное преобразование, округление, сжатие, кодирование энтропии, реализация программы, используемое программное обеспечение, описание функций, результаты выполнения программы, заключение, список использованных источников, приложение 1 – руководство пользователя, приложение 2 – блок-схема алгоритма, приложение 3 – исходный код программы. Предполагаемый объём пояснительной записки: Не менее … страниц. Дата выдачи задания: 04.02.2019 Дата сдачи реферата: 27.05.2019 Дата защиты реферата: 27.05.2019
|
||
Студент |
|
Нерсисян А.С. |
Преподаватель |
|
Фахми Ш.С. |
Аннотация
Данная курсовая работа содержит в себе реализацию дискретного косинусного преобразования исходного изображения. В первом разделе приведены теоретические основы алгоритма дискретных косинусных преобразований. Во втором разделе представлен код программы, реализованной на языке Python. В третьем разделе показаны результаты выполнения программы.
SUMMARY
This course work contains the implementation of a discrete cosine transform of the original image. The first section presents the theoretical foundations of the discrete cosine transform algorithm. The second section presents the program code implemented in the Python language. The third section shows the results of the program
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 5
1. Теоритическая часть 6
1.1. Препроцессинг 6
1.2. Дискретное косинусное преобразование 6
1.3. Округление 8
1.4. Сжатие 9
1.5. Кодирование энтропии 10
14
14
15
ЗАКЛЮЧЕНИЕ 17
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 17
ВВЕДЕНИЕ
Целью выполнения данной курсовой работы является закрепление и углубление теоретических знаний по дисциплине «Схемотехника». Задачей курсового проекта является реализация программы, выполняющей алгоритм дискретного косинусного преобразования. Данный алгоритм применяется в сжатии информации, например, в JPEG и MPEG, и тесно связан с дискретным преобразованием Фурье.
Теоритическая часть
1.1. Препроцессинг
Если изображение содержит более одной компоненты, то они кодируются по отдельности. В связи с этим, на данном этапе выполняется перевод графического изображения из его компонентного представления в цветоразностное, яркостное представление (ICT — Irreversible Color Transform). В связи с тем, что человеческий глаз более восприимчив к яркостному сигналу, чем к цветовому, это преобразование позволит добиться больших результатов сжатия при меньших визуальных потерях. Далее будет рассматриваться кодирование одной отдельной компоненты.
Помимо ICT преобразования, на данном этапе исходное изображение разбивается на малые квадратные блоки и выполняется сдвиг основания значений цвета относительно нуля для корректного пространственного представления изображения: [0,2p - 1] -> [-2p-1, 2p-1 - 1]. Эти шаги важны для эффективной работы кодера на следующем этапе.
1.2. Дискретное косинусное преобразование
Являясь ключевым шагом алгоритма сжатия, дискретное косинусное преобразование (далее ДКП) представляет собой разновидность преобразования Фурье и, также как и последнее, имеет обратное преобразование (ОДКП). Если рассматривать изображение как совокупность пространственных волн, где оси X и Y соответствуют ширине и высоте картинки, а по оси Z откладываются значения цвета соответствующих пикселей, то можно перейти от пространственного представления картинки к ее спектральному представлению и обратно. ДКП преобразует матрицу пикселей размера N x N в матрицу частотных коэффициентов соответствующего размера.
![]()
![]()
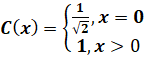
В получаемой матрице низкочастотные компоненты расположены ближе к левому верхнему углу, а более высокочастотные смещаются вправо вниз. В связи с тем, что основная часть графических образов на экране состоит из низкочастотной информации, используя полученную матрицу можно дифференцированно отбрасывать наименее важную информацию с минимальными визуальными потерями. Таким образом, ДКП позволяет выбрать информацию, которую можно безболезненно отбросить, не внося серьезных искажений в картинку. Трудно представить, как можно было бы выполнить эту задачу на исходном изображении.
Из формул видно, что вычисление одного элемента результирующей матрицы требует O(N2) времени, поэтому почти невозможно выполнить преобразование всей матрицы целиком. Группа разработчиков JPEG предложила оптимальный вариант решения этой проблемы: разбивать исходную матрицу на квадраты стандартного размера 8x8 и выполнять преобразование каждого из них. Использование блоков большего размера позволит улучшить качество сжатия, но не до бесконечности, так как слишком мала вероятность того, что сильно отдаленные точки похожи друг на друга.
Стоит отметить, что в ходе вычислений используется только 32 заранее вычисленных значения косинусов, что позволяет заметно увеличить скорость работы преобразования. Это уже, несомненно, приводит к частичной потери информации, но ее объемы относительно несущественны.
Небольшого увеличения производительности можно добиться, если при вычислениях использовать только целочисленную арифметику, что, правда, является актуальным только для старых вычислительных машин, так как в современных компьютерах стоимость операций над числами с плавающей запятой не отличается от операций над целыми. Также использование целочисленной арифметике негативно сказывается на качестве сжимаемого изображения, что делает этот метод неприемлемым для современных компьютеров. Так как ДКП является разновидностью преобразования Фурье, то все методы увеличения производительности преобразования Фурье могут быть использованы и здесь.
