36. Первообразная и неопределённый интеграл

Функция называется первообразной по отношению к функции f (x), если. F (x) дифференцируема и выполняется условие F '(x)=f(x)

Неопределенным интегралом от функции f (x) называется множество всех первообразных этих функций.Интеграл: dy/dx=2x Интегралdy= Интеграл2xdx y=x^2+C 37. Таблица неопределенных интегралов.

38. Свойства неопределенных интегралов.

1. 

2. Дифференциал от неопределённого интеграла равен подынтегральному выражению

3)Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной константы 4)Постоянный множитель можно выносить за знак интеграла

5)Неопределённый интеграл от суммы функций равен сумме неопределённых интегралов

39. Интегрирование заменой переменной. Интегрирование подстановкой (замена переменной). Пусть требуется вычислить интеграл , который не является табличным. Суть метода  подстановки состоит в том, что в интегралепеременную х заменяют переменной t по формуле x=φ(t), откуда dx=φ’(t)dt.

Теорема. Пусть функция x=φ(t) определена и дифференцируема на некотором множестве Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула:

 - 40. Интегрирование по частям неопределенных интегралов. Пусть u = u(x) и v = v(x) суть две дифференцируемые функции, заданные на одном и том же промежутке [a, b]. Тогда на этом промежутке будет (uv)' = u'v + uv'. Последнее равенство можно переписать в равносильной форме

Отсюда, замечая, что u'dx = du,  v'dx = dv, получаем:

41. Определенный интеграл и его свойства. Определенный интеграл – это приращение некоторой первообразной на отрезке (a,b).

Если для функции y=f(x) существует предел, то функция называется интегрируемой на отрезке (a,b), а предел называется определенным интегралом и обозначается

Свойство определенного интеграла:

1. .

2. .

3. ,

4. ,

5. .

6. .

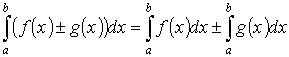42. Определенный интеграл как предел интегральной суммы в упрощенных задачах экономики.

43. Формула Лейбница-Ньютона. Формула Ньютона-Лейбница. Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции , то. 44. Замена переменной в определенном интеграле. Пусть функция φ (t) имеет непрерывную производную на отрезке [α, β], а = φ (α), b = φ (β) и функция f (x) непрерывна в каждой точке x = φ (t), где t [α, β]. Тогда справедливо равенство

. 45. Интегрирование по частям определенных интегралов.

Ели функции u и v непрерывны и имеют производную первого порядка, то справедлива формула:

. 46. Несобственные интегралы первого рода.

Опр. Несобственным интегралом с бесконечным верхним пределом от непрерывной функции f(x) на промежутке [a,+∞]называется предел

Если интеграл в правой части существует и принимает конечное значение, то интеграл называется сходящимся. Если предел не существует или равен 0, то расходящийся. 47. Несобственные интегралы второго рода.

Пусть функция ƒ(х) непрерывна на промежутке [а; b) и имеет бесконечный разрыв при х = b. Если существует конечный предел то его называют несобственным интегралом второго рода и обозначают 

Таким образом, по определению,

Если предел в правой части существует, то несобственный интеграл сходится. Если же указанный предел не существует или бесконечен, то говорят, что интеграл расходится.

Если функция ƒ(х) терпит разрыв во внутренней точке с отрезка [а; b], то несобственный интеграл второго рода определяется формулой

В этом случае интеграл слева называют сходящимся,  если оба несобственных интеграла, стоящих справа, сходятся. В случае, когда ƒ(х) > 0, несобственный интеграл второго рода  (разрыв в точке х = b) можно истолковать геометрически как площадь бесконечно высокой криволинейной трапеции.