Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Чувашский государственный университет им. И.Н. Ульянова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Классификация поверхностей второго порядка-1.doc

Скачиваний:

Добавлен:

07.02.2015

Размер:

2.02 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

§4 Основные виды поверхностей второго порядка и их свойства.

Рис. 1 Эллипсоид

Положительные числа а, b, c называются полуосями эллипса. Эллипсоид лежит внутри прямоугольного параллелепипеда -а ≤ x ≤ a , -b ≤ y ≤ a , -c ≤ z ≤ c.То есть эллипсоид является ограниченной поверхностью.

Теорема 1. Плоское сечение поверхности второго есть кривая порядка не выше двух.

Доказательство. Выберем систему координат, в которой уравнение плоскости:

Z=0. Тогда уравнение сечения G( x, y ) := F( x, y, 0 ) = 0.

Следствие 2. Непустое плоское сечение эллипсоида – эллипс или точка.

Доказательство. Это единственные не пустые ограниченные кривые 0, 1 или 2-ого порядка.

Мнимый эллипсоид не имеет ни одной вещественной точки:

Рис. 2 мнимый эллипсоид

( Изображён на рисунке 3 ) В сечении плоскостью z = 0 эллипс:

Называемый горловым. Однополостный гиперболоид обладает следующим замечательным свойством.

Определение 3. Назовём прямолинейной образующей поверхности прямую, целиком в ней содержащуюся. Как правило, это понятие не применяется к распадающимся поверхностям.

Рис. 3 однополостный гиперболоид

Доказательство. Указанные свойства аффинные, поэтому достаточно доказать теорему для гиперболоида :

x² + y² –z² = 1.

или

x² – z²=1 – y², (x–z)(x+z) = (1-y)(1+z)

Отсюда сразу видим два семейства прямолинейных образующих:

Где λ и μ – произвольные вещественные числа, не обращающиеся в нуль одновременно.

Тогда:

Так что пары плоскостей в пересечении действительно дают прямую.

Пусть точка (x₀, y₀, z₀) принадлежит гиперболоиду. Тогда, взяв для I λ = x₀ + y₀ и μ = 1 + y₀, а для II – λ = x₀+z0 и μ=1-y₀, получим прямые, проходящие через данную

точку. Поскольку одно из чисел 1 - y₀ или 1 + y₀ отлично от 0, то пара (λ, μ) определенна по точке (x₀, y₀, z₀) однозначно ( с точностью до множителя ) для каждого семейства.

Итак, через каждую точку проходит ровно одна прямая каждого семейства.

Покажем, что других образующих нет. Допустим, что образующая параллельна

плоскости z = 0, то есть содержится в плоскости z = z₀. Тогда она должна содержатся в окружности x² + y² = 1 + z²₀ что невозможно. Итак, всякая образующая пересекает z=0, а значит, и горловой эллипс ( окружность ). В силу вращательной симметрии достаточно исследовать одну его точку, например, ( 1, 0, 0 ). Пусть через нее проходит образующая с некоторым направляющим вектором ( α, β, γ ):

x=1+αt

y=βt

z=γt

так что уравнение ( результат подстановки в уравнение гиперболоида )

( α²+β²-γ²)t²+2αt=0

Должно иметь решением любое t, откуда

Значит, направляющий вектор ( с точностью до ненулевого множителя ) равен (0,1,±1), то есть имеются две возможности, а мы их уже нашли – это прямая первого

семейства и прямая второго. Итак, других образующих нет.

Из аналогичного соображения получаем, что прямые одного семейства не могут пересекаться. Пусть они параллельны одному вектору ( α, β, γ ). Значит, он параллелен каждой из четырёх плоскостей, фигурирующих в записи двух прямых семейства. Тогда он является ненулевым решением системы четырёх линейных уравнений с матрицей:

Аналогично в обратной ситуации. Значит, можно считать, что μ=μ'=1, λ и λ'

- ненулевые. Тогда для условия rk < 3 необходимо8

что в данной ситуации возможно только если λ = λ' и прямые совпадают. Итак, две прямые одного семейства скрещиваются.

Семейства не пересекаются, так как отображение ( x, y, z ) → ( -x, -y, -z ) переводит прямые одного семейства в прямые другого, параллельные своим прообразам. Действительно, если бы прямая принадлежала обоим семействам, то ее образ – так же, и тем самым, мы имели две параллельные прямые из одного семейства.

Теперь рассмотрим две прямые l₁ и l₂ из разных семейств. Пусть π – плоскость, проходящая через l₁ и некоторую точку Ρl₂ P¢ l₁ поэтому соответствующее плоское сечение гиперболоида, являясь по теореме 1 кривой порядка не старше 2, должно быть парой параллельных или пересекающихся прямых. Одна из них - l₁ а другая – некоторая прямолинейная образующая lP. Она не совпадает и не скрещивается с l₁ , поэтому, по доказанному, не может принадлежать первому семейству, а значит, принадлежит второму, и в силу единственности прямой второго семейства, проходящей через Р, совпадает с l₂ .

(изображён на рисунке 4)

Рис. 4 двуполостный гиперболоид

Плоскость z = 0 не пересекает гиперболоид и разделяет его на две части, называемые полостями.

Теорема 4. Двуполостный гиперболоид не имеет прямолинейных образующих,

Доказательство. Прямолинейная образующая не может пересекать плоскость z=0. Значит, она лежит в плоскости z = z₀ .Но соответствующее плоское сечение

ограниченно ( эллипс, точка или Ǿ ) и не может содержать прямую.

^5.).

( изображён на рисунке 5а.).

Рис. 5 Конус второго порядка

Заметим, что уравнение однородно ( второго порядка ); F( λx , λy , λz ) = λ,2F( x, y, z),

и таким образом, любая прямая, содержащая О и некоторую другую точку конуса, является прямолинейной образующей.

Определение 5.Пусть Г – произвольная кривая, лежащая в плоскости π, а точка О не

принадлежит π. Конической поверхностью над Г с центром в О называется объединение всех прямых вида ОХ , ХГ ( рисунок 5 б.). .Прямые ОХ называются образующими, а кривая Г – направляющей конической поверхности

Мнимый конус не имеет ни одной вещественной точки ( рисунок 6 )

Рис. 6 мнимый конус

Теорема 6. Коническая поверхность над эллипсом является конусом второго порядка.

Доказательство. Выберем такую систему координат с центром в О, что плоскость π задается уравнением z = h ≠ 0 ( рисунок 5 в.). Если мы выберем направления осей Ох и Оу параллельно главным осям эллипса Г, то уравнение эллипса в плоскости π примет вид:

F=(x, y) =a₁₁(x-x₀)²+a₂₂( y-y₀ )²-1=0

где 0<а₁₁<а₂₂ . Тогда уравнение конической поверхности над ним:

Ф(x, y, z) = z²F(,)=0

Действительно, точка ( x, y, z ), z ≠ 0 , принадлежит поверхности тогда и только тогда, когда точка ( (x/z)*h, (y/z)h, h ) принадлежит кривой, то есть :

F(,) =0.

Но при сделанном предположении z ≠ 0 данное уравнение равносильно выводимому. Осталось доказать, что при z = 0 выводимое уравнение определенно и его множество решений совпадает с О. Определённость следует из того, что во втором сомножителе степень ( 1 / z ) равна 2 и при умножении пропадает.

После умножения уравнение превращается ( при z = 0 ) в h²q(x, y)=0. Поскольку асимптотических направлений γ эллипса нет, то x = y = 0.

Итак,

После замены x' = x - x₀ , y' = y – y₀ , z' = z получаем

Ф( x', y', z' ) = a₁₁h²(x')²+a₂₂h²(y')²-(z')²=0

То есть конус.

( изображён на рисунке 7 а.).

Теорема 7. Эллиптический параболоид не имеет прямолинейных образующих.

Доказательство. Дословно как с двуполостным гиперболоидом.

( изображён на рисунке 7 б.).

Определение 8. Ненулевой вектор ( α, β, γ ) задаёт асимптотические направление для поверхности F = 0 , если он обнуляет квадратичную форму уравнения:

q(α, β, γ)=a₁₁α²+a₂₂β²+a₃₃γ²+2a₁₂αβ+2a₁₃αγ+2α₂₃βγ=0

Асимптотические направления не зависят от выбора системы координат.

Теорема 9. прямолинейные образующие любой поверхности имеют асимптотическое направление.

Доказательство. Пусть

-прямолинейная образующая. Подставив в уравнение F=0, получим

F₂t²+2F₁t+F₀=0 для любого t. Значит, F₂ = q( α , β , γ ) = 0

Теорема 10 . Гиперболический параболоид имеет два семейства образующих,

проходящих через каждую точку. Образующие одного семейства попарно скрещиваются и параллельны одной плоскости , разных семейств пересекаются.

Доказательство . Асимптотические направления ( α ,β , γ ) гиперболического

Параболоида находятся из уравнения , т.е. лежат в плоскостях :

π₁ : , π₁ : .

С учётом уравнения параболоида

Это означает , что имеются два семейства прямолинейных образующих

Действительно , если мы имеем образующую , параллельную , скажем, То расстояние ( со знаком ) от любой её точки допостоянно , т.е.

С некоторой константой k мы имеем

откуда из уравнения поверхности получаем второе уравнение(1). Таким образом , других Образующих нет.

Через каждую точку параболоида проходит ровно по одной образующей каждого семейства, так как определяется однозначно.

Заметим, что никакая вертикальная прямая не может быть прямолинейной образующей. Действительно , в этом случае x = const , откуда и z = const.

Два семейства не пересекаются. Действительно, предположим, что общая прямая имеет направляющий вектор

Тогда он должен удовлетворять однородной части уравнений обеих систем:

откуда α = β = 0 и прямая вертикальна, что невозможно.

Образующие одного семейства не могут пересекаться, так как это противоречило бы единственности. Они не могут быть параллельны, так как их направляющие вектора-

- ( ,,k ) с различными k. Значит, они скрещиваются, причем ( по определению)

параллельны фиксированной плоскости.

Пусть теперь l₁ и l₂ – образующие из разных семейств. Покажем, что они пересекаются. Рассмотрим плоское сечение параболоида, проходящее через l₁

и Рl₂Р¢ l₁ . Это кривая , порядка не выше двух, значит состоящая из двух прямых l₂ и l. Предположим l ≠ l₂ причем они пересекаются ( в точке Р ) . Значит, l не принадлежит второму семейству, то есть принадлежит первому. Но тогда она должна скрещиваться с l₁ и не может лежать с ней в одной плоскости. Значит, l = l₂. Допустим, l₁║ l₂ . Тогда координаты ( α, β, γ ) удовлетворяют уравнениям:

откуда α = β = 0 и образующая вертикальна, что невозможно.

Вернёмся к гиперболоидам. Их асимптотический конус определяется уравнением:

Из уравнения однополостного гиперболоида имеем для положительных z:

а из уравнения ( 21 ) -

откуда:

Аналогично для двуполостного.

Предложение 11.Асимптотические направления ( α, β, γ ) однополостного гиперболоида совпадают с направлениями образующих его асимптотического конуса и являются решениями (21).

Доказательство. По определению асимптотических направлений.

Теорема 12. Никакие три различных прямолинейных образующих однополостного гиперболоида из одного семейства не параллельны одной плоскости. Любые три попарно скрещивающиеся прямые, не параллельные одной плоскости, являются прямолинейными образующими некоторого однополостного гиперболоида.

Доказательство. Рассмотрим три прямолинейных образующих из одного семейства. Допустим, они параллельны одной плоскости. Так как центральное плоское сечение ( асимптотического ) конуса состоит из двух пересекающихся одной прямой, то две из трёх прямых должны быть параллельны. Противоречие.

Рассмотрим три попарно скрещивающиеся прямые и некоторую аффинную систему координат, в которой они имеют вид:

Следующая квадрика содержит все эти прямые:

(x-x₁)(y-y₃)(z-z₂)-(x-x₂)(y-y₁)(z-z₃)=0

Это действительно квадрика, так как коэффициент при х³ равен нулю, а , скажем, при ху равен –z₂+z₃≠0 так как прямые скрещиваются. Из классификации квадрик и доказанных свойств следует, что это – однополостный гиперболоид ( у цилиндров таких образующих не может быть, это мы докажем в следующем предложении 14 )

Рассмотрим теперь не распадающиеся цилиндры

Предложение 14. Все прямолинейные образующие не распадающихся цилиндров являются их образующими ( образующие цилиндров определяются по аналогии с коническими поверхностями ) и, следовательно, параллельны между собой

Доказательство. Рассмотрим произвольную прямолинейную образующую и спроектируем ее на плоскость z = 0 . Тогда результат проекции должен целиком принадлежать направляющей ( конике ) , что возможно только тогда , когда проекция – точка, то есть прямолинейная образующая параллельна оси Oz, то есть образующим.

Рис. 8 эллиптический цилиндр

Рис. 9 мнимый эллиптический цилиндр

Рис. 10 две мнимые пересекающиеся плоскости

Рис. 11 гиперболический цилиндр

Рис. 12 две пересекающиеся плоскости

Рис. 13 параболический цилиндр

Рис. 14 две параллельные плоскости

Рис. 15 две мнимые параллельные плоскости

Рис. 16 две совпадающие плоскости

Приложение 1

Задача 1.

Какую поверхность определяет уравнение:

Решение. Чтобы привести данное уравнение к каноническому виду выделяем полные квадраты по x , y , z :

Отсюда:

Сравнивая это уравнение с каноническими выясним что это уравнение однополостного гиперболоида , центр которого смещён в точку О`( -1 ; 1 ; -2 ) если ввести обозначения :

то уравнение примет вид :

Новые оси O`X , O`Y и O`Z параллельны старым . Так как a = c = 2 то это однополостный гиперболоид вращения вокруг оси О`Y . Относительно новых осей гиперболоид имеет вид :

Рис. 17

Задача 2.

Исследовать форму и расположение относительно системы координат поверхности:

4 – z = x² + y²

Решение. Применим метод сечений. Полагая в данном уравнение z = h получим

x²+y²=4-h

отсюда следует что 4- h должна быть величиной неотрицательной . Пусть 4 – h = R*R , получим в сечении плоскостью z = h линию :

x²+y²=R² ; z = h

Эта линия, очевидно, является окружностью радиуса R с центром на оси Oz. Следовательно данная поверхность является поверхностью вращения вокруг оси Oz . Чтобы выяснить вращением какой линии она получается , пересечём поверхность плоскостью x = 0 . В сечении получится парабола на плоскости yOz

y²=4-z ; x=0 ;

Вершина её лежит в точке ( 0 , 0 , 4 ) а направлена парабола в отрицательную сторону оси Oz. Таким образом исследуемая поверхность параболоид вращения :

Рис. 18

Задача 3.

Показать , что уравнение :

Определяет однополостный гиперболоид вращения вокруг оси Oy.

Решение. Рассмотрим сечение данной поверхности плоскостями y = h перпендикулярными оси Оу. В сечении получим линию:

, где

Таким образом , в любом сечении , перпендикулярном оси Оу , получается окружность радиуса R , то есть данная поверхность есть поверхность вращения вокруг оси Оу. Выясним , вращением какой линии получена эта поверхность . Пересечём поверхность какой-либо плоскостью , проходящей через ось вращения , например плоскостью хОу , в сечении получится линия:

Эта есть гипербола с полуосями а , b . Вращаясь вокруг оси Оу , она и образует данную поверхность , являющуюся поэтому однополостным гиперболоидом вращения вокруг оси Оу.

Рис. 19

Задача 4.

Найти точки пересечения эллипсоида

с прямой

при

при каком значении а прямая касается эллипсоида ?

Решение. Запишем параметрические уравнения данной прямой :

x = 1 ; y = 1 + t ; z = a*t.

Подставляя значения x , y , z в уравнение эллипсоида :

получим квадратное уравнение для t :

из которого находим значения параметра t , отвечающие точкам пересечения прямой с эллипсоидом :

при получатся два значения :

следовательно точки пересечения следующие :

Если прямая касается эллипсоида , то должно быть , а это произойдёт

В том случае , если подкоренное выражение равно нулю .

Значит при прямая является касательной.

Задача 5.

Исследовать сечения эллипсоида

плоскостями

Решение. Рассмотрим сначала сечение эллипсоида плоскостями z = h , где

Подставляя в уравнение эллипсоида получим :

Отсюда

Вводя обозначения

видим , что в сечении получится эллипс

С полуосями . При получаем

Таким образом , наибольший получается в сечении плоскостью хОу. Если поднимать или опускать эту плоскость вдоль оси Oz параллельно плоскости xOy, то размеры сечений уменьшаются до тех пор , пока при z=3 z=-3 не превратятся в точку (0,0,3) или ( 0 , 0 , -3 ). При дальнейшем увеличении h плоскость эллипсоида пересекать уже не будет, так как корень, входящий в выражения для станет мнимым .

В сечении плоскостями, параллельными xOz и yOz , будут также получаться эллипсы . В частности , в сечении координатными плоскостями

y = 0 и x = 0 получатся наибольшие по размерам эллипсы :

Проведённое исследование позволяет сделать вывод , что эллипсоид является

овальной поверхностью:

Рис. 20

Задача 6.

Какую поверхность определяет уравнение

Решение. Эта поверхность есть гиперболический цилиндр с образующими,

параллельными оси оХ. В самом деле, данное уравнение не содержит х,

а направляющая цилиндра есть гипербола

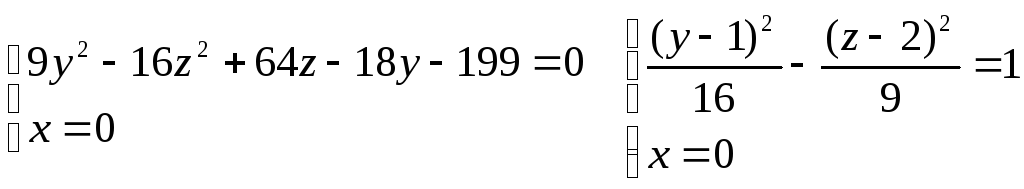
с центром в точке ( 0 , 1 , 2) и действительной осью , параллельной оси Оу.

Приложение 2.

Задача 1.8.

Составить уравнения сторон треугольника, если А( -5 ; 5 ) и В( 3 ; 1 ) две его вершины, а D( 2 , 5 ) – точка пересечения высот.

Решение:

Уравнение АВ ( как прямая проходящая через две точки) :

; x + 5 = -2( y - 5 ) ; АВ: -0.5x + 2.5 = y.

Чтобы найти AC, найдём сначала BD:

;

BD: -4x + 13 = y.

Так как BD_┴AC то κκ₁ = -1 , где κ = -4 , и значит κ₁ = 0.25 . ( κ и κ₁ угловые коэффициенты BD и AC) .

AC: y = 0.25x + b; b найдем исходя из того что AC проходит через точку А( -5;5)

5 = +b ; b = 6.25 ; AC: y=0.25x + 6.25

Чтобы найти уравнение прямой ВС вначале найдём уравнение DH_ab потом через их пересечения найдём точку С и потом искомую прямую СВ.

κκ₁ = -1 , где κ = -0.5 для АВ, и значит κ₁ = 2 . y = 2x + b . DH_ab пересекает D( 2;5)

то есть 5 = +b , b = 1, DH_ab : y = 2x + 1.

y = 2x + 1

y = 0.25x + 6.25

2x – 0.25x + 1 – 6.25 = 0 ; x = 3 ; y = + 1 = 7 ; значит С( 3 ; 7 )

; 6( x – 3) = 0( y - 1 ) ; x = 3.

Значит CB : x = 3.

Рис. 21

Ответ:

AC: y = 0.25x + 6.25 ;

АВ: y = -0.5x + 2.5 ;

CB : x = 3 .

Задача 2.8 .

Даны вершины треугольника АВС. Найти длины медианы, высоты, биссектрисы, проведённых из вершин А, найти угол при вершине В. ( назовём углом φ )

А(10 ; -1) В(-2 ; -6) С(-6 ; -3)

Решение:

АМ медиана, М( Х_м ; У_м ) , Х_м = (-6 – 2 )/2 = -4 ; У_м = (-3 - 6)/2 = -4,5

│АМ│=

СВ:-0,75x – 7,5 = y ;

ρ( А, ВС ) =│АН│= == 11,2

│AH│=11,2 – длина высоты.

AD – биссектриса, значит λ = AB/АC ;

AB=АС=

x_D= ( -2+(-6)*( 0,05 260 )/(1 + 0,05 260 ) ; y_D= ( -6-3*( 0,05 260 )/(1 + 0,05 260 ) ;

CB : -0,75x-7,5

BA : ; (5/12)*x – (62/12) = y ;

κ = - 0,75 ; κ₁ = 5/12 ;

cos φ = = ( -14/12 ) / ( 65/48 ) ≈ -0,861538461…

φ ≈ arccos(-0,86153846) = 120⁰

Ответ : АМ медиана, равна 208,25 ≈ 14,439…

АН высота, равна 11,2

AD биссектриса равна ≈ 15,745

φ внутренний угол равен ≈ 120⁰

( треугольник ABC изображён на следующей странице на рисунке 22)

Рис. 22

Задача 4.8 .

Найти точки пересечения кривой второго порядка γ с прямой α :

γ: x²-2xy+y²-4x+4=0.

α: x+y-2=0.

Решение:

y = -x+2; x²-2xy+y²-4x+4= (x-y)²-4x+4= (2x+2)²-4x+4=4x²-8x+4-4x+4=0

x²-3x+2=0;

D=3²-2*4=1;

x_1,2= (3±1) / 2 ; x₁= 2/2=1 ; x₂= 4/2=2

y₁= -1+2=1 ; y₂= -2+2=2

Значит точки пересечения кривой второго порядка γ с прямой α это точки А(1;1) и В(2; 0)

Ответ: А(1;1) и В(2; 0)

Задача 7.8.

Для векторов: и, заданных в ортонормированном базисеR( O, ,,) найти :

1. Направляющие косинусы вектора ;

2. Площадь параллелограмма, построенного на векторах и, имеющих общее начало.

3. Объём пирамиды, построенной на векторах ,,, имеющих общее начало.

Решение:

1. α β и γ есть углы между ортами e₁ e₂ e₃ вектора . Значитcos α , cos β , cos γ направляющие косинусы этого вектора. ( рисунок 23)

Рис. 23

;

2. Площадь параллелограмма построенного на векторах равна модулю их векторного произведения.

Рис. 24

3. Объём пирамиды равен одной шестой от объёма параллелепипеда, а объём параллелепипеда равен смешанному произведению трёх векторов, на которых он основан.