
Министерство образования и науки Российской Федерации
Федеральное государственное образовательное учреждение высшего профессионального образования
«Чувашский государственный университет имени Ульянова»
Кафедра высшей математики
Курсовая работа на тему:
«Классификация поверхностей второго порядка»
Введение.
В этой работе содержится материал по поверхностям второго порядка. Что такое квадрика ( или поверхность второго порядка ), даны все возможные семнадцать видов квадрик, их канонические формулы, изображения и основные свойства.
Уделено внимание возможным видам любого многочлена второй степени в пространстве, возможным видам квадрики ( доказывается что их всего семнадцать).
Затронуты свойства эллипсоида, однополостного и двуполостного гиперболоидов, конуса второго порядка, гиперболического параболоида. Рассматриваются прямолинейные образующие у отдельных видов поверхностей второго порядка. Приведено решение типичных задач.
§1 Поверхности второго порядка.
Поверхности второго порядка задаются в некоторой аффинной системе координат уравнением:
F(x,y,z) = a11x² + a22y² + a33z² + 2∙a12xy + 2∙a13xz + 2∙a23yz +
└─────────────┬───────────────┘
q( x, y, z) квадратичная часть
+ 2∙a1x + 2∙a2y + 2∙a3z + a0 = 0
└─────┬────┘
L ( x, y, z ) однородная линейная часть
При этом требуется , чтобы квадратичная часть была отлична от нуля. Если ввести обозначения:


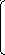

|
|
a11 |
a12 |
a13 |
|
|
a11 |
a12 |
a13 |
a1 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
Q:= |
a12 |
a22 |
a23 |
, |
A:= |
a12 |
a22 |
a23 |
a2 |
, |
L:= |
(a1, |
a2 |
a3) |
.X:= |
|
y |
|
|
|
|
|
|
|
a13 |
a23 |
a33 |
|
|
a12 |
a23 |
a33 |
a3 |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
a2 |
a3 |
a0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
то уравнение примет вид:
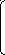

x
XTQX + LX + a0 = (x,y,z,1)A y
z
1
Определение. Алгебраической поверхностью второго порядка (квадрикой) называется поверхность S, уравнение которой в декартовой прямоугольной системе координат имеет вид:
![]() ,
,
где по крайней мере одна из шести величин A, B, C, D, E, F не равна нулю. Если это уравнение не удовлетворяется ни одной действительной точкой x=(x1, x2, x3), то говорят, что оно определяет мнимую поверхность.
Теорема Пусть в некоторой прямоугольной системе координат задана квадратичная часть q(x, y, z). Тогда найдется другая прямоугольная система с тем же началом , в которой квадратичная часть примет диагональный вид:
q (x′, y′, z′) + λ1(x′)2+ λ 2(y′)2+ λ 3(z′)2
где λ1,λ2,λ3- собственные значения Q , то есть корни характеристического многочлена :
Xq(λ)=det(Q- λE)=0,
а новые базисные вектора e'1 e'2 e'3 являются соответствующими собственными векторами. В частности , все собственные значения вещественны , а собственные вектора , отвечающие различным собственным значениям , ортогональны.
Лемма. Для любого многочлена второй степени в пространстве существует прямоугольная система координат , в которой он принимает один из следующих пяти видов :
(I) F= λ1x2 + λ2y2 + λ3z2 + τ (λ1 λ2 λ3 ≠0);
(II) F=λ1x2 + λ2y2 + 2b3z (λ1 λ2 b3≠0);
(III) F= λ1 x2 + λ2 y2+ τ (λ1 λ2 ≠0);
(IV) F= λ1 x2 + 2c2y (λ1 c2 ≠0);
(V) F= λ1 x2 + τ (λ1 ≠0);
Доказательство. В силу предыдущей теоремы можем найти такую прямоугольную систему , в которой квадратичная часть диагональна , то есть:
F= λ1x2 + λ2y2 + λ3z2 + 2b1x + 2b2y + 2b3z + b0=0
Рассмотрим все возможные случаи.
При λ1 λ2 λ3 ≠0 имеем:
F=λ1( x + b1/ λ1 )2 +λ1 ( y + b2 / λ2 )2 + λ3(x + b3 / λ3)2 + ( b0 – (b1)2/ λ1 - (b2)2/ λ2 -
- (b3)2/ λ3) = λ1(x')2 + λ2(y')2 + λ3(z')2 + τ.
(II) При λ3 =0 и λ1 λ2 b3 ≠ 0 имеем:
F = λ1(x+b1/ λ1 ) 2 + λ1(y+ b2/ λ2) 2 + 2b3z + ( b0 – (b1)2/ λ1 - (b2)2/ λ2)=
=λ1(x')2 + λ2(y')2 + 2b3z + τ = λ1x2 + λ2y2 + 2b3( z+ τ /2b3)= λ1x2 + λ2y2 + 2b3z'.
(III) При λ3= b3 =0 и λ1 λ2 ≠ 0 имеем:
F = λ1(x+b1/ λ1) 2 + λ1 (y+ b2/ λ2) 2 + ( b0 – (b1)2/ λ1 - (b2)2/ λ2)=
= λ1(x')2 + λ2(y')2 + τ.
(IV) При λ3= λ 2=0 , λ1≠0 и хотя бы один из b2 и b3 не равен нулю. Тогда имеем:
F = λ1(x + b1/ λ1) 2+ 2b2y + 2b3z + ( b0 – (b1)2/ λ1) = λ1(x')2 + 2c2y'.
Где:
x' = x + b1/ λ1 , c2 = ( (b2)2+(b3)2 )1 / 2
y' = ( (b2)2 +(b3)2 )-1/2 ( b2y + b3z + 1/2( b0 – (b1)2/ λ1 ))
z'=( (b2)2 +(b3)2 )-1/22 ( – b3y + b2z ).
Такая “нормировка” функций перехода гарантирует ортогональность соответствующей матрицы и, тем самым ортогональность замены.
Если же b2 = b3 = 0 , то мы сразу имеем выражение конечного вида.
Пусть λ3 = λ2 = b2 = b3 = 0 и λ1 ≠0. Тогда имеем:
F = λ1(x + b1/ λ1) 2 + ( b0 – (b1)2/ λ1 ) = λ1(x')2 + τ.
Лемма доказана.


