Применение общего уравнения динамики.

1.

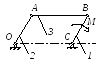
Пара сил с постоянным моментом М =0,8 Нм приводит в движение механизм, расположенный в горизонтальной плоскости. Кривошипы 1 и 2 – однородные стержни длиной l = 0,2 м и массой m₁ = m₂ = 1 кг, масса m₃ = 2 кг. Определить угловое ускорение кривошипа 1.

2.

Тела 1 и 2 – однородные диски, массы и радиусы которых одинаковы. Определить ускорение тела 3, если его масса m₃ = m₁ = m₂.

3.

Определить ускорение центра С оси катка 1, если тела 1 и 2 – однородные сплошные цилиндры с одинаковыми массами и радиусами.

4.

Определить угловое ускорение барабана 1 , если к нему приложена пара сил с постоянным моментом М = 0,2 Нм, массы тел m₁ = m₂ = 1 кг, моменты инерции относительно центральных осей I₁ = I₂ = 0,02 кг м², радиусы r₁= r₂= 0,2 м.

5.

Система состоит из подвижного и неподвижного блоков одинаковой массы m и радиуса r и связывающего эти блоки нерастяжимого невесомого каната. Пренебрегая трением, определить, какой вращающий момент М_вр необходимо приложить к неподвижному блоку, чтобы обеспечить подъем подвижного блока с заданным ускорением w. Блоки считать однородными круглыми дисками.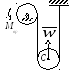

6.

На трех сплошных однородных валах, к каждому из которых приложен вращающий момент М, находится балка массой m₂. Определить ускорение балки, если масса каждого вала равна m₁, а радиус равен r, считая, что между валами и балкой скольжение отсутствует. Трением в осях пренебречь.

7.

Два сплошных однородных вала 1 и 2 массами m₁ и m₂ вращаются без трения около параллельных осей при помощи бесконечного ремня так, что скольжение отсутствует. К первому валу приложен вращающий момент М, а на второй вал наматывается трос, к концу которого привязан груз массой m₃. Определить ускорение груза. Радиус вала 1 равен r.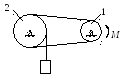

8.

Момент инерции жестко скрепленных между собой шкивов, насаженных на общую ось, равен I =0,3 кг м², а их радиусы r₁ = 0,2 м; r₂ = 0,1 м. Груз массы m₁ = 1 кг падает отвесно и сообщает вращение шкивам; при этом второй груз такой же массы скользит по шероховатой горизонтальной плоскости. Определить коэффициент трения скольжения f этого груза по плоскости, если ускорение падающего груза w₁ = 0,1 g.

Применение уравнений Лагранжа второго рода.

1.

Физический маятник состоит из однородного прямолинейного стержня ОА длины L и закрепленного на свободном конце точечного груза А. Пренебрегая сопротивлениями, определить обобщенную силу Q_φ, соответствующую углу φ отклонения маятника от положения его устойчивого равновесия, если веса стержня и груза одинаковы и равны Р.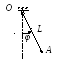

2.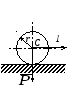

Колесо веса Р радиуса r катится по горизонтальной плоскости без проскальзывания под действием горизонтальной силы , приложенной к центру С этого колеса. Выбирая в качестве обобщенной координаты угол поворота φ колеса, определить обобщенную силу Q_φ, если коэффициент трения качения равен δ.

3.

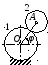
Эпициклический механизм состоит из неподвижного зубчатого колеса 1, кривошипа ОА массы 3m и длины l и подвижного колеса 2 массы m. Выбирая в качестве обобщенной координаты угол поворота φ кривошипа ОА, определить коэффициент инерции механизма. Колесо 2 считать однородным сплошным диском.

4.

Тележка скатывается без скольжения по наклонной плоскости, образующей с горизонтом угол α. Масса тележки без колес равна М, масса всех колес - m. Считая колеса однородными сплошными дисками, определить ускорение тележки. Трением качения, а также трением в осях пренебречь. Для решения использовать уравнения Лагранжа второго рода.

5.

Однородный стержень длиной l = 3 м и массой m = 30 кг вращается в вертикальной плоскости. Определить обобщенную силу, соответствующую обобщенной координате φ, в момент времени, когда угол φ = 45°.

6.

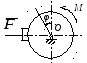
К цилиндру радиуса R, который вращается под действием пары сил с моментом М = 20 Нм, прижимается тормозная колодка силой F = 100 Н. Определить обобщенную силу, соответствующую углу φ поворота тела. Коэффициент трения скольжения колодки о цилиндр f = 0,1.

7.

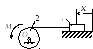
Тело 1 массой m = 30 кг и цилиндр 2 радиуса R = 0,25 м соединены нерастяжимым тросом. Определить обобщенную силу, соответствующую обобщенной координате x, если коэффициент трения скольжения между телом 1 и поверхностью f = 0,2, а к цилиндру приложена пара сил с моментом М = 25 Нм.

8.

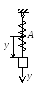
Груз массой m = 6 кг подвешен на пружине, при деформации которой возникает восстанавливающая сила F = -300 y. Определить координату y, при которой обобщенная сила Q_y равна нулю. Точка А является концом пружины в недеформированном состоянии.

9.

Определить угловое ускорение катка 2, катящегося без скольжения, если на блок 1 действует пара сил с моментом М = 0,6 Нм. Каток 2 считать однородным цилиндром массы m = 4 кг. Радиусы тел 1 и 2 равны r = 0,5 м.

Материальная точка М массой m = 1 кг равномерно движется по окружности со скоростью v = 4 м/c. Определить модуль импульса равнодействующей всех сил, действующих на эту точку за время ее движения из положения 1 в положение 2.