Уравнения равновесия плоской и пространственной систем сил

Существуют три вида уравнений равновесия плоской системы сил. Первый, основной вид вытекает непосредственно из условий равновесия:

;

и записывается так:

; ; .

Два других вида уравнений равновесия также могут быть получены из условий равновесия:

; ; ,

где прямая ABне перпендикулярна осиx;

; ; .

Точки A, B и Cне лежат на одной прямой.

В отличие от плоской системы сил условиями равновесия произвольной пространственной системы сил являются два векторных равенства:

.

Если эти соотношения спроецировать на прямоугольную систему координат, то получим уравнения равновесия пространственной системы сил:

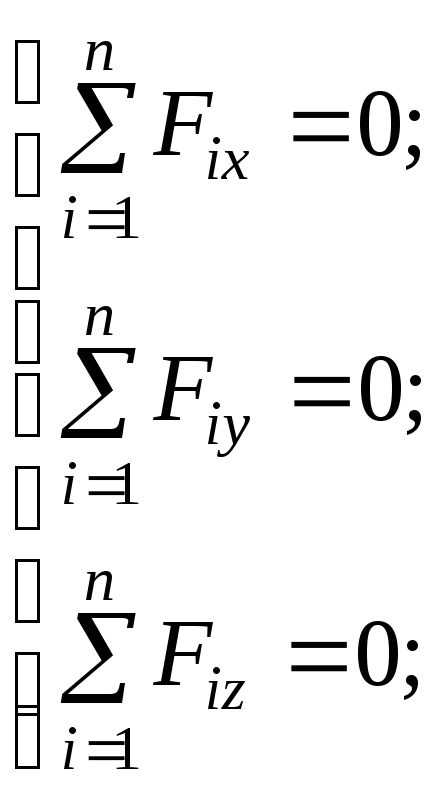
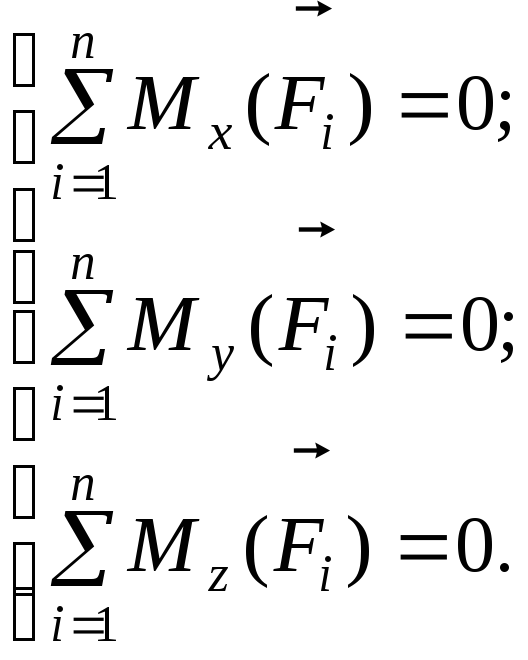
Задание 1. Определение реакций опор составной конструкции (Система двух тел)

Конструкция состоит из двух ломаных стержней ABC иCDE, соединенных в точкеCнеподвижным цилиндрическим шарниром и прикрепленных к неподвижной плоскостиxOy либо с помощью неподвижных цилиндрических шарниров (НШ), либо подвижным цилиндрическим шарниром (ПШ) и жесткой заделкой (ЖЗ). Плоскость качения подвижного цилиндрического шарнира составляет уголс осьюOx.Координаты точкиA, B, C,D иE,а также способ крепления конструкции приведены в табл. 1. Конструкция загружена равномерно распределенной нагрузкой интенсивностиq, перпендикулярной участку ее приложения, парой сил с моментомMи двумя сосредоточенными силами и . Равномерно распределенная нагрузка приложена таким образом, что ее равнодействующая стремится повернуть конструкцию вокруг точкиO против хода часовой стрелки. Участки приложенияq иM, а также точки приложения и , их модули и направления указаны в табл. 2. Единицы задаваемых величин: q – килоньютон на метр (кН/м);M– килоньютон-метр (кНм); и – килоньютон (кН);ипредставлены в градусах, а координаты точек – в метрах. Углы,иследует откладывать от положительного направления осиOxпротив хода часовой стрелки, если они положительны, и по ходу часовой стрелки – если отрицательны.

Определите реакции внешних и внутренней связей конструкции.

Указания к выполнению задания

На координатной плоскости xOyв соответствии с условием варианта задания (табл. 1) необходимо построить точкиA,B, C,D,E; изобразить ломаные стержниABC,CDE; указать способы крепления этих тел между собой и с неподвижной плоскостьюxOy. Затем, взяв данные из табл. 2, загрузить конструкцию двумя сосредоточенными силами и , равномерно распределенной нагрузкой интенсивностиqи парой сил с алгебраическим моментом M. Так как в задании исследуется равновесие составного тела, далее нужно построить еще один рисунок, изобразив на нем отдельно телаABCи CDE. Внешние (точкиA,E) и внутреннюю (точкаС) связи на обоих рисунках следует заменить на соответствующие реакции, а равномерно распределенную нагрузку – на равнодействующую (l– длина участка приложения нагрузки), направленную в сторону нагрузки и приложенную к середине участка. Поскольку рассматриваемая конструкция состоит из двух тел, то для нахождения реакций связей нужно составить шесть уравнений равновесия. Существуют три варианта решения этой задачи:

а) составить три уравнения равновесия для составного тела и три – для тела ABC;

б) составить три уравнения равновесия для составного тела и три – для тела CDE;

в) составить по три уравнения равновесия для тел АВСиCDE.

Пример

Дано:A (0;0,2);В (0,3:0,2);С (0,3:0,3);D (0,7:0,4);E (0,7:0); кН/м, кН, β = - 45˚, и кН, γ = - 60˚,кНм.

Определитьреакции внешних и внутренней связей конструкции.

Решение. Разобьем конструкцию (рис. 7,а) в точкеСна составные частиABCиCDE(рис. 7,б,в). Заменим шарнирыAиBсоответствующими реакциями, составляющие которых укажем на рис. 7. В точкеCизобразим составляющие - сил взаимодействия между частями конструкции, причем.

Таблица 1

Варианты задания 1

Вариант	Точка A		Точка B		Точка C		Точка D		Точка E		Способ крепления конструкции
	xA	yA	xB	yB	xC	yC	xD	yD	xE	yE	т. A	т. E	
1	0,0	0,0	0,6	0,4	1,1	0,4	1,1	1,0	1,5	1,0	ЖЗ	ПШ	30˚
2	0,0	0,4	0,6	0,4	0,6	0,8	1,0	0,2	1,6	0,2	НШ	НШ	-
3	0,0	0,0	0,6	0,4	0,6	0,8	1,4	0,8	1,4	0,2	ПШ	ЖЗ	0˚
4	0,0	1,2	0,6	0,8	0,6	0,4	1,4	0,4	1,4	0,0	ЖЗ	ПШ	60˚
5	0,0	0,4	0,6	0,4	0,6	0,0	1,2	0,0	1,2	1,0	НШ	НШ	-
6	0,0	0,0	0,6	0,0	0,6	0,4	1,4	0,0	1,4	0,6	ПШ	ЖЗ	-30˚
7	0,0	1,2	0,6	0,8	1,1	0,8	1,1	0,3	1,6	0,3	ЖЗ	ПШ	30˚
8	0,0	0,0	0,6	0,0	0,6	0,4	1,4	0,8	1,4	0,2	НШ	НШ	-
9	0,2	0,4	0,8	0,4	1,4	0,8	1,4	1,2	0,5	1,2	ПШ	ЖЗ	-45˚
10	0,2	0,2	0,2	0,8	0,6	0,8	1,4	0,5	1,4	1,1	ПШ	ЖЗ	30˚
11	0,0	0,6	0,8	0,6	1,0	1,3	1,4	1,3	1,4	0,2	ЖЗ	ПШ	60˚
12	0,6	0,0	0,6	0,6	0,2	0,6	0,8	1,2	1,6	1,2	НШ	НШ	-
13	0,0	1,2	0,4	1,2	0,8	0,3	1,4	0,3	1,4	1,0	ПШ	ЖЗ	90˚
14	0,2	1,2	0,2	0,4	0,6	0,4	1,4	1,0	1,4	0,2	ЖЗ	ПШ	90˚
15	0,0	0,8	0,9	0,8	1,6	0,5	1,6	0,2	0,4	0,2	НШ	НШ	-
16	1,1	0,7	1,1	0,2	0,2	0,2	0,6	1,2	1,3	1,2	ЖЗ	ПШ	30˚
17	0,0	0,2	0,6	1,0	1,0	1,0	1,0	0,4	1,4	0,4	НШ	НШ	-
18	1,4	0,3	1,4	0,8	0,9	0,8	0,3	0,2	0,3	1,3	ПШ	ЖЗ	30˚
19	0,0	1,2	0,4	0,5	0,4	0,1	1,2	0,1	1,2	1,0	ЖЗ	ПШ	-90˚
20	1,5	0,9	1,5	0,3	0,8	0,3	0,2	0,6	0,2	1,2	НШ	НШ	-
21	0,0	0,2	1,4	0,6	1,4	1,2	0,4	1,2	0,4	0,7	ПШ	ЖЗ	0˚
22	1,0	1,0	1,6	1,0	1,6	0,2	0,6	0,2	0,3	0,8	ПШ	ЖЗ	-30˚
23	0,0	0,6	0,5	1,2	0,8	1,2	0,8	0,3	1,6	0,3	НШ	НШ	-
24	1,0	0,2	1,6	0,2	1,6	1,0	0,3	0,5	0,3	1,2	ЖЗ	ПШ	90˚
25	0,0	0,0	1,3	0,6	1,3	1,2	0,2	1,2	0,2	0,7	ПШ	ЖЗ	0˚
26	1,6	1,2	1,1	1,2	1,1	0,2	0,2	0,0	0,2	0,5	НШ	НШ	-
27	0,0	0,4	1,0	1,2	1,4	1,2	1,4	0,2	0,7	0,2	ЖЗ	ПШ	-60˚
28	1,6	0,3	1,1	0,3	1,1	0,8	0,3	1,4	0,3	0,3	ПШ	ЖЗ	30˚
29	0,0	0,0	1,1	0,7	0,4	0,7	0,4	1,4	1,4	1,5	НШ	НШ	-
30	1,4	1,2	0,8	1,1	1,6	1,1	0,3	0,2	0,3	0,7	ЖЗ	ПШ	90˚

Таблица 2

Данные к заданию 1

Группа	Нагрузка q		Сила			Сила			Момент M
	Участок	Значение	Точка	Значение	Угол β	Точка	Значение	Угол γ	Участок	Значение
1	AB	1	B	2	30˚	D	3	-45˚	CD	-2
2	BC	4	D	3	45˚	B	2	60˚	DE	2
3	CD	2	B	4	60˚	D	1	30˚	AB	-3
4	DE	2	D	1	-30˚	B	4	-60˚	BC	4
5	AB	3	B	5	-60˚	D	2	30˚	DE	3
6	BC	3	D	2	-45˚	B	5	-30˚	CD	1

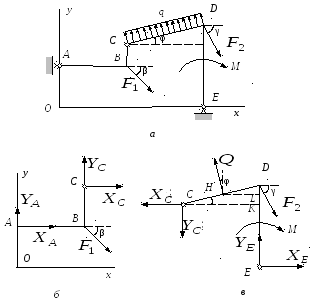
Рис. 7

Равномерно распределенную нагрузку интенсивности q заменим равнодействующей, кН:

.

Вектор образует с положительным направлением осиyугол φ, который несложно найти по координатам точекC иD (см. рис. 7,а):

Для решения задачи воспользуемся первым видом уравнений равновесия, записав их отдельно для левой и правой частей конструкции. При составлении уравнений моментов выберем в качестве моментных точек точки A– для левой иE– для правой частей конструкции, что позволит решить эти два уравнения совместно и определить неизвестные и .

Уравнения равновесия для тела ABC:

,

где .

Представим силу как сумму составляющих:, где. Тогда уравнения равновесия для телаCDEмогут быть записаны в виде

,

где

.

Решим совместно уравнения моментов, предварительно подставив в них известные значения.

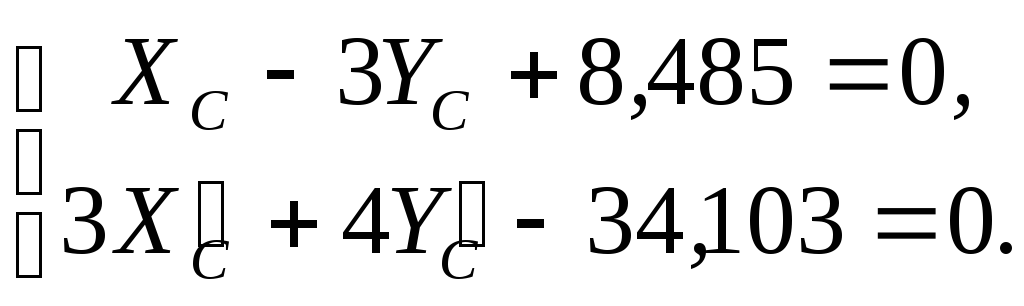
Учитывая, что по аксиоме о равенстве сил действия и противодействия , из полученной системы найдем, кН:

Тогда из оставшихся уравнений равновесия тел ABC и CDE несложно определить реакции внутренней и внешних связей, кН:

,

,

,

.

Результаты вычислений представим таблицей:

-8,086 кН	-1,753 кН	4,958 кН	4,647 кН	5,258 кН	4,581 кН