11. Обчислити площу фігури, обмеженої лініями:

Визначимо абсцису точки А:

,

, .

Тоді .

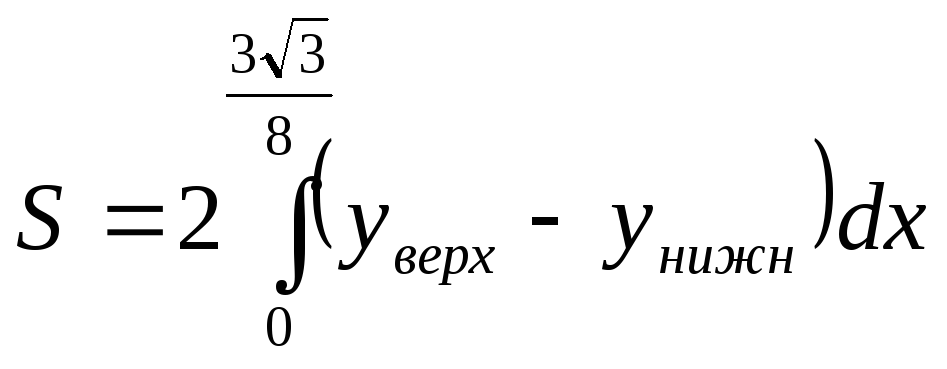Тут ,,,

x	0		.
t

12. Обчислити довжину дуги кривої, заданої рівнянням

,

13. Обчислити невласні інтеграли або довести їх розбіжність:

а) б).

, таким чином, інтеграл збігається до числа .

Інтеграл розбігається.

Умови обов'язкового домашнього завдання 1

Варіант 1

1. Обчислити границі числових послідовностей:

а) ;

б) ;

в) ;

г) .

2. Довести, що , тобто за заданимвизначити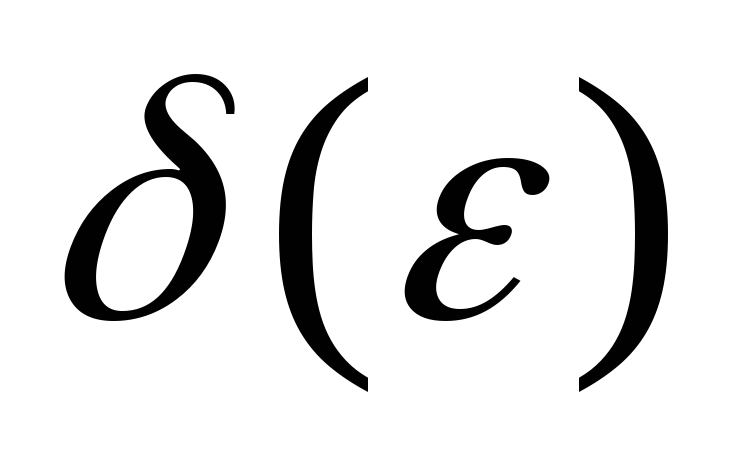, якщо

.

3. Використовуючи таблицю еквівалентних, обчислити границі функцій:

а) ;

б) ;

в) ;

г) ;

д) .

4. Дослідити дану східчасту функцію на неперервність і побудувати її графік:

5. Виходячи з визначення похідної, знайти , якщо

.

6. Знайти похідні таких функцій:

а);

б);

в);

г).

7. Знайти похідну другого порядку від функції, заданої параметрично:

8. Провести повне дослідження функції й побудувати графік:

.

8. Знайти невизначені інтеграли:

a);

б) ;

в) ;

г) .

8. Обчислити визначені інтеграли:

а) ;

б) ;

в);

г) .

8. Обчислити площу фігури, обмеженої лініями:

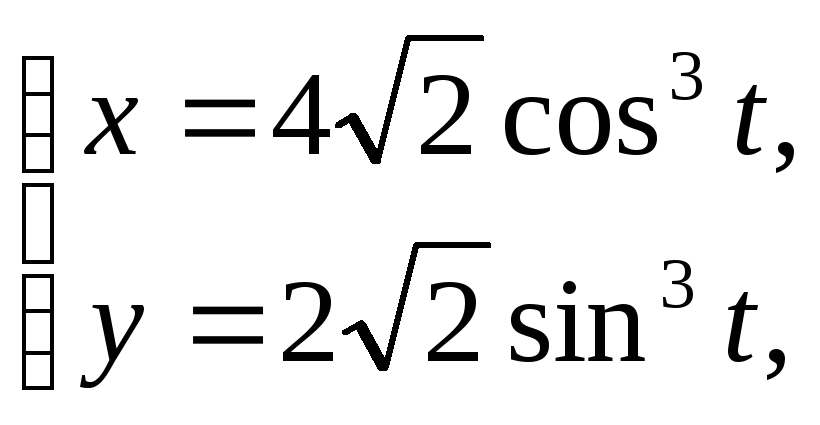
8. Обчислити довжину дуги кривої, заданої рівнянням

= 3е^3/4, -.

8. Обчислити невласні інтеграли або довести їх розбіжність:

а) ; б).

Варіант 2

1. Обчислити границі числових послідовностей:

а) ;

б) ;

в) ;

г) .

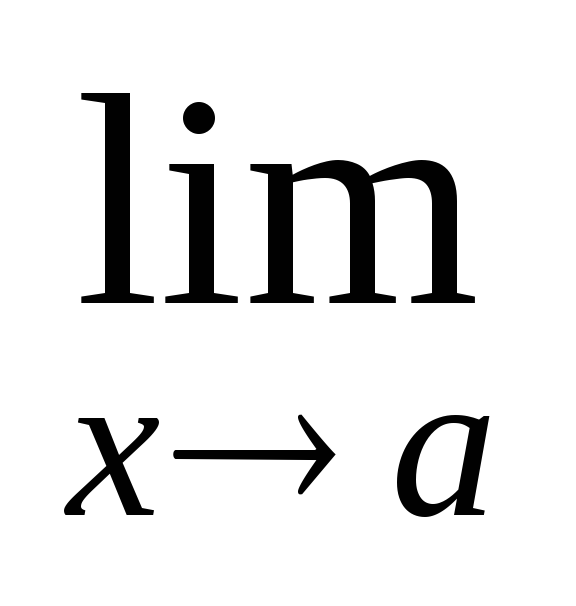
2. Довести, що, тобто за заданимвизначити, якщо

.

3. Використовуючи таблицю еквівалентних, обчислити границі функцій:

а) ;

б) ;

в) ;

г) ;

д) .

4. Дослідити дану східчасту функцію на неперервність і побудувати її графік:

5. Виходячи з визначення похідної, знайти , якщо

6. Знайти похідні таких функцій:

а) ;

б) ;

в) ;

г).

7. Знайти похідну другого порядку 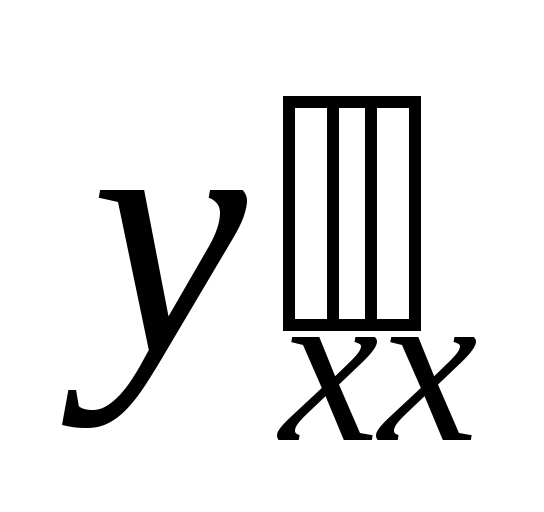від функції, заданої параметрично:

8. Провести повне дослідження функції й побудувати графік:

.

9. Знайти невизначені інтеграли:

а) ;

б) ;

в) ;

г) .

10. Обчислити визначені інтеграли:

а) ;

б) ;

в) ;

г) .

11. Обчислити площу фігури, обмеженої лініями:

12. Обчислити довжину дуги кривої, заданої рівнянням

ρ = 2е^4/3, -.

13. Обчислити невласні інтеграли або довести їх розбіжність:

а) ; б).

Варіант 3

1. Обчислити границі числових послідовностей:

а) ;

б) ;

в) ;

г) .

2. Довести, що , тобто за заданимвизначити, якщо

.

3. Використовуючи таблицю еквівалентних, обчислити границі функцій:

а) ;

б) ;

в);

г) ;

д) .

4. Досліджувати дану східчасту функцію на неперервність і побудувати її графік:

5. Виходячи з визначення похідної, знайти , якщо

6. Знайти похідні таких функцій:

а) ;

б) ;

в) ;

г) .

7. Знайти похідну другого порядку від функції, заданої параметрично:

8. Провести повне дослідження функції й побудувати графік:

.

9. Знайти невизначені інтеграли:

а) ;

б) ;

в) ;

г) .

10. Обчислити визначені інтеграли:

а);

б) ;

в) ;

г).

11. Обчислити площу фігури, обмеженої лініями:

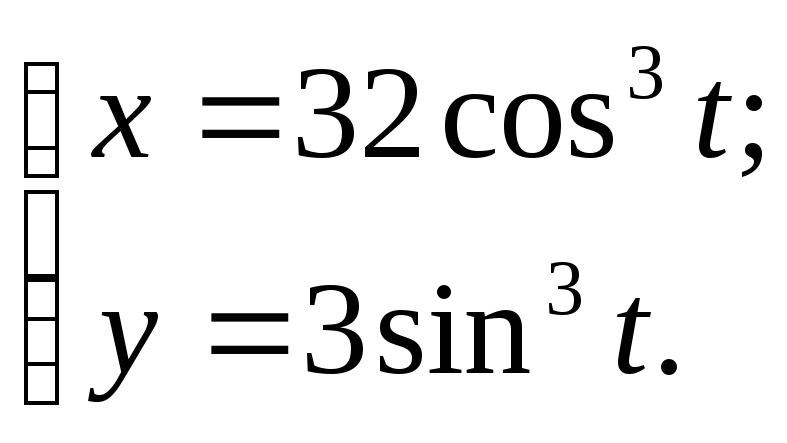
12. Обчислити довжину дуги кривої, заданої рівнянням:

.

12. Обчислити невласні інтеграли або довести їх розбіжність:

а) ; б).