
- •Методичні завдання репродуктивного та творчого характеру (для самостійної роботи)
- •Література
- •Тема 3.5. Чотирикутники, многокутники, вписані та
- •Змістову структуру теми запропоновано у таблиці 1.
- •Контрольно-смислові запитання та завдання репродуктивного характеру (перша самооцінка)
- •Відповіді та вказівки до контрольно-смислових запитань і завдань репродуктивного характеру
- •Історична довідка
3. Постановка задачі.
Задача.
Побудувати
бісектрису кута
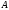 .
.
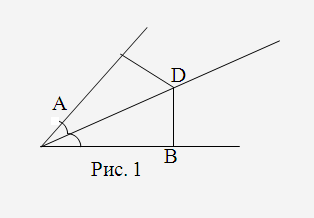
Аналіз
Нехай
бісектрису кута
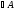 побудовано (Рис. 1). Позначимо на ній
точку
побудовано (Рис. 1). Позначимо на ній
точку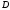 ,
відмінну від
,
відмінну від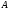 .
Виберемо на різних сторонах кута точки
.
Виберемо на різних сторонах кута точки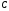 і
і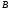 .
Сполучимо їх з точкою
.
Сполучимо їх з точкою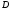 .
Отримали
.
Отримали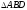 і
і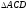 .
Якщо
.
Якщо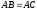 і
і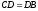 ,
то
,
то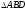 =
=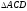 ,
а тому
,
а тому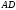 –
бісектриса.
–
бісектриса.
Побудова
З вершини
 даного кута, як із центра, опишемо коло
довільного радіуса. Нехай
даного кута, як із центра, опишемо коло
довільного радіуса. Нехай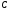 і
і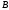 –
точки перетину його зі сторонами кута
(Рис. 2).
–
точки перетину його зі сторонами кута
(Рис. 2).Побудуємо ще два кола з тим самим радіусом з центрами
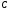 і
і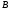 .
Нехай
.
Нехай –
точка їх перетину.
–
точка їх перетину.Проведемо бісектрису
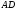 даного кута.
даного кута.
4. Виконання вчителем кожного етапу побудови окремо на окремому рисунку (рис. 3–5).
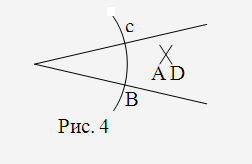
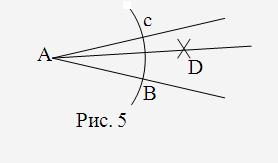
5. Складання з учнями алгоритму побудови відповідно до виконаних окремих етапів, розв’язаної задачі на побудову бісектриси кута трикутника.
Алгоритм побудови бісектриси кута
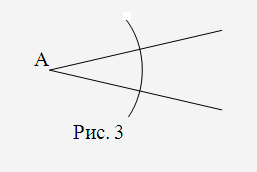
Щоб побудувати бісектрису кута треба:
Описати з вершини кута, як із центра, коло довільного радіуса.
З точок перетину побудованого кола із сторонами кута описати два коли тим самим радіусом і позначити точку їх перетину відмінну від вершини кута.
Через вершину кута і точку перетину, кіл провести промінь, який і є бісектрисою кута.
6. Самостійне виконання учнями побудови в зошитах за складеним алгоритмом.
11.
В основі методу геометричних місць
лежить поняття геометричного місця
точок. Суть методу геометричних місць
точок полягає в тому, щоб знайти деяку
точку, що задовольняє дві незалежні
умови. Нехай першій умові задовольняють
точки фігури
 ,
другій умові задовольняють точки фігури
,
другій умові задовольняють точки фігури .
Шукана точка належить фігурам
.
Шукана точка належить фігурам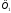 і
і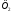 одночасно і є точкою їх перетину.
одночасно і є точкою їх перетину.
12. Під час ознайомлення учнів з методом геометричних місць точок доцільно використати алгоритмічний підхід, тобто розв’язавши одну-дві вдало дібраних задач виділити правило-орієнтир методу.
Проілюструйте це на прикладі.
Задача
1. Дано
три точки:
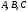 .
Побудуйте точку
.
Побудуйте точку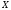 ,
яка однаково віддалена від точок
,
яка однаково віддалена від точок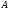 та
та
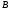 і
знаходиться на даній відстані від точки
і
знаходиться на даній відстані від точки
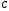 .
.
Проаналізувавши
умову задачі, слід зосередити увагу
учнів на тому, що шукана точка
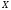 задовольняє дві умови:
задовольняє дві умови:
однаково віддалена від точок
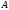 та
та
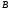 ;
;знаходиться на даній відстані від точки
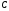 .
.
Геометричне
місце точок, що задовольняє першу умову
є пряма, перпендикулярна відрізку
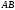 ,
що проходить через його середину.
,
що проходить через його середину.
Геометричне
місце точок, що задовольняє другу умову
є коло даного радіусу з центром в точці
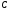 .
.
Шукана
точка
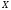 лежить на перетині цих геометричних
місць.
лежить на перетині цих геометричних
місць.
Записане на дошці розв’язання задачі доцільно ще раз проаналізувати, виділити етапи та сформулювати правило-орієнтир методу геометричних місць точок. Воно може бути таким:
Щоб розв’язати задачу методом геометричних місць точок треба:
З’ясувати, до знаходження якої точки (точок) зводиться розв’язування задачі і які дві вимоги ця точка має задовольняти.
Відкинути одну з вимог задачі і побудувати геометричне місце точок, що задовольняють другу вимогу.
Відкинути другу вимогу і побудувати геометричне місце точок, що задовольняють першу вимогу.
Позначити шукану точку як перетин побудованих геометричних місць.
Задача 2. Побудуйте трикутник за стороною і проведеними до неї медіаною і висотою.
Короткий запис умови
Дано:
 –
сторона трикутника;
–
сторона трикутника;
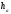 –висота
трикутника проведена до сторони а;
–висота
трикутника проведена до сторони а;
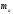 –медіана
трикутника, проведеного до сторони а;
–медіана
трикутника, проведеного до сторони а;
Побудувати:
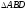
Аналіз
Припустимо,
що задача розв’язана. Нехай
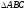 –
шуканий, у нього сторона
–
шуканий, у нього сторона
 ,
висота
,
висота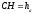 ,
медіана
,
медіана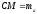 .
.
Дві
вершини цього трикутника визначаються
кінцями даної сторони, тобто відрізка,
довжина якого
 .
Третя вершина визначиться такими
умовами:
.
Третя вершина визначиться такими
умовами:
Знаходиться на відстані
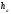 від сторони
від сторони ,
тобто є геометричним місцем точок
площини, що віддалені від заданої прямої
на відстань
,
тобто є геометричним місцем точок
площини, що віддалені від заданої прямої
на відстань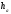 ;
це пара прямих, паралельних даній
прямій, що знаходяться від неї на
відстані
;
це пара прямих, паралельних даній
прямій, що знаходяться від неї на
відстані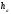 .
.Знаходиться на відстані
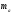 від середини сторони
від середини сторони ,
тобто є геометричним місцем точок
площини, що рівновіддаленій від даної
точки; це коло з центром в середині
відрізка і радіусом
,
тобто є геометричним місцем точок
площини, що рівновіддаленій від даної
точки; це коло з центром в середині
відрізка і радіусом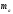 .
.
Отже,
третя вершина трикутника – це точка
перетину кола з центром у середині
відрізка та радіусом
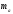 і парою прямих, паралельних даній прямій,
що знаходяться на відстані
і парою прямих, паралельних даній прямій,
що знаходяться на відстані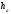 від неї.
від неї.
Побудова
Будуємо відрізок
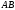 довжиною
довжиною .
.Будуємо пряму паралельно прямі
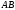 на відстані
на відстані
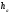 від неї.
від неї.Знаходимо середину відрізка
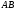 –
точку
–
точку
 .
.Будуємо коло з центром в точці
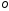 і радіусом
і радіусом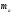 .
.Знаходимо точку перетину прямих з колом.
Будуємо
 (рис.
6).
(рис.
6).
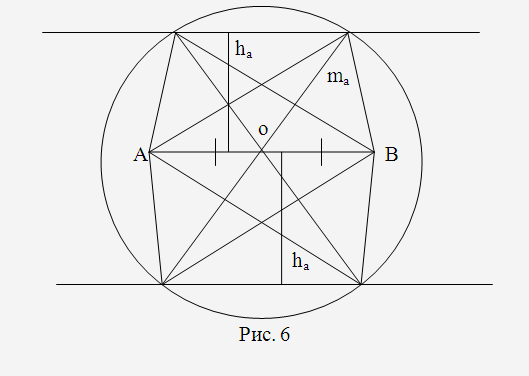
Доведення
Трикутник
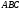 –
шуканий, тому що:
–
шуканий, тому що:
Сторона трикутника
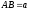 .
.Медіана трикутника
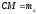 .
.Висота трикутника
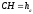 .
.
Дослідження
Задача має розв’язок, якщо медіана більша за висоту. Усього буде чотири розв’язки, але всі трикутники при цьому будуть рівні. Тому за шуканий розв’язок приймають тільки один з чотирьох рівних трикутників. Якщо довжина висоти і медіана одна і та сама, то розв’язком задачі будуть два рівних рівнобедрених трикутника, які також приймаються за один розв’язок.
13. Суть алгебраїчного методу полягає в тому, що розв’язування задачі на побудову зводиться до побудови деякого відрізка (або відрізків), величину якого (яких) виражають через величини відомих відрізків за допомогою формули. Тобто шуканий відрізок будують за одержаною формулою. Виникає питання, чи завжди відрізок,. Заданий формулою, можна побудувати за допомогою циркуля і лінійки. На це питання дає відповідь теорема.
Теорема. Відрізок XV можна побудувати за відомими відрізками лінійкою і циркулем тоді і тільки тоді, коли його довжина виражається через довжину відомих відрізків і раціональні числа за допомогою скінченої кількості раціональних операцій (операцій додавання, віднімання, множення та ділення) та добування квадратних коренів (див. додаток [1]).
У шкільному курсі математики загальноосвітньої школи термін «алгебраїчний метод» використовується рідко, але у неявному вигляді метод представлений в діючих підручниках з геометрії основної школи.
14. опорними задачами для алгебраїчного методу є задачі на побудову відрізка х, довжина якого знаходиться за формулами:
1)
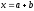 ,
де
,
де та
та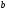 –
довжини даних відрізків;
–
довжини даних відрізків;
2)
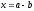 ,
де
,
де та
та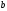 –
довжини даних відрізків;
–
довжини даних відрізків;
3)
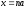 ,
де
,
де є
є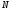 ,
, –
довжини даних відрізків;
–
довжини даних відрізків;
4)
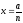 (ділення
відрізка на п рівних частин),
де
(ділення
відрізка на п рівних частин),
де
 –
довжини даних відрізків.
–
довжини даних відрізків.
Будуємо
промінь з початком у точці
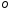 ,
що є одним із кінців даного відрізка
,
що є одним із кінців даного відрізка ,
під довільним кутом до нього. Відкладаємо
на побудованому промені від точки
,
під довільним кутом до нього. Відкладаємо
на побудованому промені від точки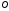
 разів
довільний відрізок
разів
довільний відрізок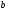 так, щоб
так, щоб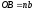 .
Сполучаємо точку
.
Сполучаємо точку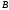 з
другим кінцем
з
другим кінцем
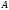 відрізка
відрізка
 .
Через точку
.
Через точку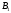 ,
що визначається умовою
,
що визначається умовою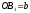 ,
проведемо пряму паралельну
,
проведемо пряму паралельну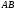 ,
яка перетинає відрізок в точці
,
яка перетинає відрізок в точці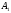 (ця
задача розв’язана в підручнику О. В.
Погорєлова після вивчення теореми
Фалеса 8 кл.).
(ця
задача розв’язана в підручнику О. В.
Погорєлова після вивчення теореми
Фалеса 8 кл.).
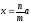 ,
де
n
і
т
– дані натуральні числа. Поділимо
відрізок а на т
рівних частин і збільшимо одержаний
відрізок в п разів (комбінація
3-ї та 4-ї побудов).
,
де
n
і
т
– дані натуральні числа. Поділимо
відрізок а на т
рівних частин і збільшимо одержаний
відрізок в п разів (комбінація
3-ї та 4-ї побудов).
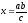 (побудова
відрізка, четвертого пропорційного
трьом даним відрізкам).
Запишемо умову у вигляді пропорції
(побудова
відрізка, четвертого пропорційного
трьом даним відрізкам).
Запишемо умову у вигляді пропорції
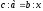 .
Нехай
.
Нехай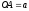 ,
,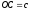 .
Члени одного відношення, відкладемо на
одному промені, що виходить з точки
.
Члени одного відношення, відкладемо на
одному промені, що виходить з точки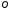 ,
а на другому промені, що виходить з тієї
самої точки, відкладаємо відомий член
другого відношення
,
а на другому промені, що виходить з тієї
самої точки, відкладаємо відомий член
другого відношення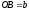 .
Через точку
.
Через точку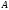 проводимо пряму, паралельну
проводимо пряму, паралельну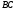 ,
що перетинається з прямою
,
що перетинається з прямою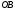 у точці
у точці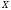 .
Відрізок
.
Відрізок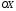 –
шуканий, тобто
–
шуканий, тобто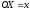 (Цій
задачі присвячено окремий пункт у
підручнику О. В. Погорєлова після вивчення
теореми про пропорційні відрізки у 8
кл.)
(Цій
задачі присвячено окремий пункт у
підручнику О. В. Погорєлова після вивчення
теореми про пропорційні відрізки у 8
кл.)
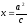 .
Можна скористатись побудовою 6, поклавши
.
Можна скористатись побудовою 6, поклавши
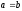 .
.
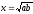 (побудова
середнього пропорційного двох даних
відрізків).
Будуємо відрізки
(побудова
середнього пропорційного двох даних
відрізків).
Будуємо відрізки
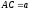 ,
,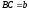 ,
так щоб
,
так щоб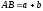 .
На
.
На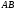 ,
як на діаметрі, будуємо півколо. У точці
,
як на діаметрі, будуємо півколо. У точці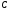 ставимо
перпендикуляр до
ставимо
перпендикуляр до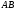 ,
перетинається з колом у точці
,
перетинається з колом у точці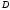 .
Тоді
.
Тоді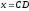 (Ця
задача є в підручнику О. В. Погорєлова,
8 кл. у темі «Теорема Піфагора»).
(Ця
задача є в підручнику О. В. Погорєлова,
8 кл. у темі «Теорема Піфагора»).
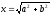 Відрізок
х будується як гіпотенуза прямокутного
трикутника з катетами
Відрізок
х будується як гіпотенуза прямокутного
трикутника з катетами
 та
та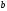 .
(Ця
задача є в підручнику О. В. Погорєлова,
8 кл. у темі «Теорема Піфагора»).
.
(Ця
задача є в підручнику О. В. Погорєлова,
8 кл. у темі «Теорема Піфагора»).
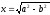 Відрізок
х будується як катет прямокутного
трикутника з гіпотенузою
Відрізок
х будується як катет прямокутного
трикутника з гіпотенузою
 та
та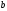 .
(Ця
задача є в підручнику О. В. Погорєлова,
8 кл. у темі «Теорема Піфагора»).
.
(Ця
задача є в підручнику О. В. Погорєлова,
8 кл. у темі «Теорема Піфагора»).
15. Застосування алгебраїчного методу, проілюструємо на прикладі такої задачі.
Задача.
Побудуємо
трикутник за сторонами
 ,
,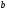 та бісектрисою
та бісектрисою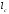 .
.
Розв’язання
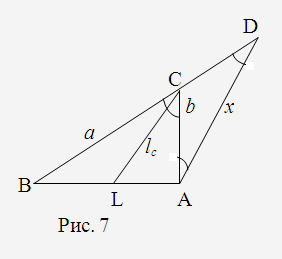
Аналіз
показує, що коли через точку
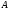 провести пряму, паралельну бісектрисі
провести пряму, паралельну бісектрисі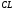 і
продовжити сторону
і
продовжити сторону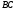 до перетину з цією прямою у точці
до перетину з цією прямою у точці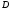 ,
то утвориться рівнобедрений трикутник
,
то утвориться рівнобедрений трикутник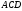 .
Нехай
.
Нехай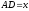 .
Оскільки трикутники
.
Оскільки трикутники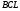 та
та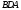 подібні, то
подібні, то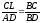 ,
або
,
або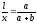 ,
,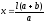 .
Побудувавши відрізок
.
Побудувавши відрізок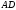 ,
можна побудувати трикутник
,
можна побудувати трикутник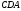 ,
а потім і трикутник
,
а потім і трикутник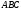 (Рис. 7).
(Рис. 7).
За записом розв’язання задачі на дошці доцільно ще раз його проаналізувати і сформулювати правило-орієнтир алгебраїчного методу. Воно може бути таким:
Скласти рівняння за умовою задачі, в якому встановлюється залежність між даними елементами і шуканими.
Розв’язати одержане рівняння відносно букви, яка позначає довжину невідомого відрізка, тобто невідомі виразити через відомі.
Дослідити одержану формулу.
Побудувати відрізок за одержаною формулою.
Довести, що одержана формула задовольняє всі умови і вимого задачі.
16. Розглядаючи задачі на побудову варто звернути увагу учнів на інші можливі методи розв’язування цих задач. Зокрема під час вивчення геометричних перетворень можна ознайомити учнів з методом геометричних перетворень розв’язування задач на побудову. Суть методу геометричних перетворень полягає в тому, що під час розв’язування задачі, перш за все на етапі аналізу, разом з даними та шуканими фігурами розглядаються інші фігури, які отримують або з даних, або шуканих фігур, або з їх частин за допомогою геометричного перетворення. Залежно від того, яке саме геометричне перетворення вибрано, говорять про той чи інший різновид методу геометричних перетворень: метод осьової симетрії, паралельного перенесення, повороту, подібності і т. д.
17. Пояснити суть застосування методу геометричних перетворень можна на прикладі наведених вище задач.
а) Осьова симетрія. Під час аналізу задачі буває доцільно для всієї фігури або її частини побудувати фігуру, симетричну їй. Після такої побудови іноді можна виявити таку залежність між елементами фігур, яку раніше важко було помітити.
Задача
1.
Побудувати трикутник
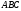 ,
знаючи дві його бічні сторони
,
знаючи дві його бічні сторони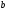 та
та
 і
різницю кутів
і
різницю кутів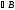 та
та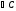 .
.
Розв’язання
Припустимо, що трикутник – шуканий (Рис. 8).
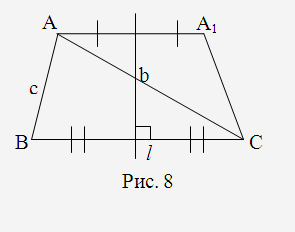
Якщо
побудувати точку
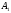 симетричну
симетричну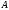 відносно
серединного перпендикуляра
відносно
серединного перпендикуляра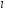 до відрізка
до відрізка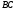 ,
то одержимо рівнобедрену трапецію
,
то одержимо рівнобедрену трапецію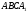 і трикутник
і трикутник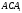 .
Для побудови шуканого трикутника
достатньо побудувати трикутник
.
Для побудови шуканого трикутника
достатньо побудувати трикутник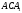 за двома сторонами
за двома сторонами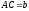 ,
,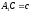 і кутом між ними
і кутом між ними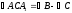 .
Потім виконати обернене перетворення:
побудувати точку, симетричну точці
.
Потім виконати обернене перетворення:
побудувати точку, симетричну точці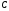 відносно серединного перпендикуляра
до відрізка
відносно серединного перпендикуляра
до відрізка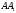 .
.
Так,
використання осьової
симетрії
звело розв’язання даної задачі до
розв’язування допоміжної задачі, в
якій потрібно побудувати трикутник за
двома сторонами і кутом між ними. У цьому
випадку метою використання осьової
симетрії є введення в малюнок даного
кута, рівного
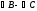 (який
без такого перетворення зобразити на
рисунку було б неможливо).
(який
без такого перетворення зобразити на
рисунку було б неможливо).
Узагальнити розв’язання даної задачі можна, сформулювавши таке правило-орієнтир використання методу осьової симетрії під час розв’язування задач на побудову:
Припустити, що задача розв’язана. Обрати певну симетрію відносно або даної прямої, або прямої, яку легко побувати. Замінити один з даних елементів симетричним щодо обраної осі симетрії.
Розв’язати задачу для побудованого симетричного елемента і решти даних. Цим самим задача зведеться або до відомої, або до простішої.
Від допоміжної задачі перейти до заданої шляхом оберненого перетворення.
б) Після переміщення будь-якого відрізка паралельно своєму початковому положенню утворюється допоміжна фігура, яку легко побудувати та елементи якої можна використати для основної побудови, крім того його (відрізка) нове положення разом з початковим буде утворювати пару протилежних сторін паралелограма, чим також доцільно скористатися під час розв’язання деяких задач.
Задача 2. Побудувати рівнобедрену трапецію за двома сторонами та діагоналлю.
Розв’язання
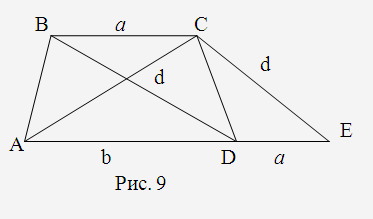
Нехай
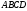 – шукана трапеція.
– шукана трапеція.
Перенесемо
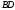 паралельно самій собі в
паралельно самій собі в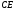 (Рис. 9). В отриманому після переміщення
в трикутнику
(Рис. 9). В отриманому після переміщення
в трикутнику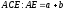 ,
,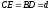 ,
,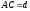 .
Трикутник
.
Трикутник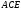 може бути побудований за трьома сторонами.
Побудувавши його, легко знайти
може бути побудований за трьома сторонами.
Побудувавши його, легко знайти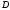 та
та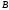 .
.
Використавши
паралельне
перенесення
діагоналі
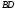 ,
ми звели розв’язування даної задачі
до допоміжної, в якій потрібно побудувати
трикутник за трьома сторонами.Метою
використання паралельного перенесення
є зміщення діагоналі
,
ми звели розв’язування даної задачі
до допоміжної, в якій потрібно побудувати
трикутник за трьома сторонами.Метою
використання паралельного перенесення
є зміщення діагоналі
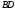 є таке положення, в якому допоміжний
трикутник
є таке положення, в якому допоміжний
трикутник
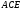 будується простіше.
будується простіше.
в) Задача 3. Через дану точку провести січну до даного кола так, щоб її внутрішня частина мала задану довжину.
Розв’язання
Припустимо,
що задачу розв’язано,
тобто побудовано січну
 до даного кола, яка проходить через дану
точку
до даного кола, яка проходить через дану
точку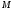 ,
а її внутрішня частина має довжину
,
а її внутрішня частина має довжину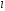 .
.
Повернувши
січну
 навколо центра кола на деякий кут,
одержимо січна
навколо центра кола на деякий кут,
одержимо січна
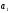 ,
внутрішня частина якої має довжину
,
внутрішня частина якої має довжину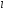 ,
але вона не проходить через дану точку
,
але вона не проходить через дану точку
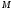 .
Якщо побудувати січну
.
Якщо побудувати січну
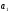 ,
а потім виконати поворот у зворотному
напрямку, то одержимо шукану січну. Кут
оберненого повороту дорівнює куту
,
а потім виконати поворот у зворотному
напрямку, то одержимо шукану січну. Кут
оберненого повороту дорівнює куту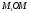 ,
де
,
де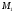 –
образ точки
–
образ точки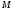 при обертанні січної
при обертанні січної навколо точки
навколо точки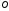 .
.
Метою
використання повороту є переміщення
січної
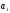 в задане положення (проходить через
задану точку
в задане положення (проходить через
задану точку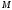 ).
).
Завершити розв’язання задачі варто узагальненням, сформулювавши правило-орієнтир використання методу повороту під час розв’язування задач на побудову.
Припустити. Що задачу розв’язано. Одним з даних елементів повернути навколо даної точки певний кут. Результатом такого перетворення буде допоміжна фігура, яку можна побудувати за даними задачі.
Побудувати допоміжну фігуру й оберненим поворотом виконати побудову шуканої фігури.
г) У багатьох задачах на побудову умову задачі вдається розділити на дві такі частини, що одна цілком визначає формулу шуканої фігури, а інша визначає її розмір. Застосування методу геометрії полягає в тому, що спочатку за тими елементами, які визначають форму фігури, будують фігуру, подібну шуканій, а потім за допомогою перетворення подібності надають її той розмір, який відповідає другій частині задачі.
Задача
4.
Побудувати трикутник за двома кутами
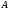 та
та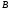 і медіаною
і медіаною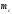 .
.
Розв’язання
За
двома кутами
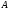 та
та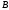 можна побудувати трикутник
можна побудувати трикутник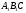 ,
подібний даному.
,
подібний даному.
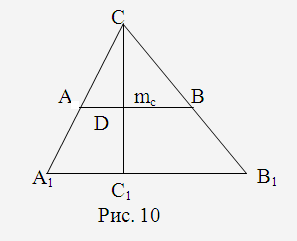
Якщо
за центр гомотетії взяти вершину
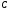 (Рис.
10), то перетворення подібності можна
виконати так: на медіані
(Рис.
10), то перетворення подібності можна
виконати так: на медіані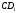 побудованого
трикутника відкладаємо відрізок
побудованого
трикутника відкладаємо відрізок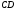 ,
що дорівнює
,
що дорівнює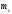 ,
і через точку
,
і через точку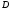 проводимо пряму, паралельну
проводимо пряму, паралельну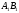 ,
яка перетинає прямі
,
яка перетинає прямі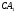 і
і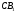 в точках
в точках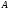 та
та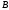 .
Трикутник
.
Трикутник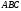 –
шуканий.
–
шуканий.
Правило-орієнтир методу гомотетії можна сформулювати так:
Виділити в умові задачі дві частини і, відкинувши ту, що визначає розміри фігури, побудувати фігуру, геометричну шуканій.
Ввести відкинуту умову і. застосовуючи перетворення гомотетії допоміжної фігури, побудувати шукану фігуру.
Методичні завдання репродуктивного та творчого характеру (для самостійної роботи)
Порівняйте місце та вимоги до математичної підготовки учнів щодо геометричних побудов в загальноосвітніх і профільних математичних класах.
Проаналізуйте діючі альтернативні підручники з геометрії для основної школи на предмет вивчення геометричних побудов.
Як відбувається пропедевтика вивчення геометричних побудов у курсі математики 5-6 класів?
Запропонуйте прикладні задачі (5-6 задачі) на застосування геометричних побудов.
З’ясуйте можливість і місце використання історичного матеріалу, цікавих фактів під час вивчення геометричних побудов.
Запропонуйте методичну схему формування поняття «геометричне місце точок». Порівняйте, як введено це поняття в діючих підручниках.
Запропонуйте дворівневу систему задач на побудову (10-12 задач) на застосування методу:
а) геометричних місць точок;
б) алгебраїчного методу;
в) геометричних перетворень.
Проаналізуйте і порівняйте системи задач на побудову на застосування методу у діючих підручниках з геометрії для основної школи. Зробіть висновки.
З’ясуйте можливості та місце використання сучасних програмних засобів під час розв’язування задач на побудову.
З’ясуйте можливості і доцільність проведення дослідження в задачах на побудову у курсі геометрії основної школи.
Література
Аргунов Б. І., Балк М. Б. Элементарная геометрия. – М., 1966. – С. 268.
Александров І. Геометричні задачі на побудову і методи їх розв’язання. – К.: Рад. школа, 1937. – 211 с.
Алябев А. В. Геометрические построения двусторонней линейкой// Математика в школе, 1978. – № 2. – С. 77-80.
Базылев В. Т., Дуничев К. И. Геометрия – II. – М.: Просвещение, 1975.
Бевз Г. П. Методика викладання математики: навч. посібник. – К.: Вища школа, 1989. – 367 с.
Бурда М. І. Навчання учнів 6-8 класів проводити дослідження в задачах на побудову // Методика викладання математики. – К.: Рад. школа, 1983. – Вип. 14. – С. 38-45.
Бурда М. І. Розв’язування задач на побудову в 6-7 класах. –К.: Рад. школа, 1986. – 112 с.
Костовский А. Н. Геометрические построения одним циркулем. –М.: Наука, 1984. – 80 с.
Кушнір І. А. Методики розв’язання задач з геометрії: кн. для вчителя. – К.: Абрис, 1994. – 464 с.
Математика. Навчальна програма для учнів 5-9 класів загальноосвітніх навчальних закладів. Сайт Міністерства освіти і науки, молоді та спорту України [Електронний ресурс]. – Режим доступу: http^//www.mon.gov.ua/images/education/average/new_pr/math.dos
Методика розв’язання задач на побудову / ред.. О. М. Астряба, О. С. Смогоржевського. – К.:Рад. школа, 1962. – 387 с.
Практикум з розв’язування задач. Геометрія / І. ф. Тесленко, В. М. Боровик, І. С. Матюшко, Е. В. Рафаловський. – К.: Рад. школа, 1978. – 206 с.
Смогоржевский А. С. Линейка в геометрических построениях. – Гостехиздат, 1957. – 64 с.
Слєпкань З. І. Методика навчання математики: підруч. Для студ. Мет. Спеціальностей вищ. Навч. Закладів. – 2-ге вид. доп. І перероб. – К.: Вища школа, 2006. – 582 с.
Тесленко І. Ф. Геометричні побудови. – К.: Рад. школа, 1956. – 140 с.
Чашечникова Л. Г., Петренко С. В., Чашечникова О. С. Геометричні побудови на площині. – Суми: Видавництво «Ярославна», 1999. – 108 с.
Четверухин Н. Ф. Методы геометрических построений. – М.: Учпедгиз, 1952. – 147 с.
