Файловый архив студентов. Файловый архив студентов.
1262 вуза, 4625 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Ярославский Государственный Педагогический Университет им. К.Д.Ушинского
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Математика

.pdf
Скачиваний:
15
Добавлен:
06.02.2015
Размер:
3.17 Mб
Скачать
☆

Пример. Если x sin

1

,

x , то при х 0 lim

 

не существует, т.е. функция

x

 

 

 

x 0

 

и несравнимы.

 

 

 

 

 

Свойства эквивалентных бесконечно малых.

1) ~ ,

 

 

 

lim

 

1

 

x a

 

 

 

 

 

 

 

 

 

2) Если ~ и ~ , то ~ ,

lim

 

lim

 

 

 

 

1 1 1

 

 

 

 

 

 

 

 

 

 

 

 

 

x a

x a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

3) Если ~ , то ~ ,

lim

lim

1

 

 

 

 

 

 

 

 

 

x a

x a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4) Если ~ 1 и ~ 1

и lim

k , то и lim 1

k

или lim

lim 1 .

 

x a

 

 

x a

1

 

x a

x a

1

 

 

 

 

 

 

 

 

 

 

Следствие: а) если ~ 1

и lim

 

k , то и lim

 

lim

1

 

 

 

 

 

x a

x a

 

x a

б) если ~ 1

и lim

k , то lim

lim

 

 

 

 

 

 

 

 

x a

 

x a

 

x a

1

 

 

 

 

 

 

 

 

 

 

 

 

 

Свойство 4 особенно важно на практике, т.к. оно фактически означает, что предел отношения бесконечно малых не меняется при замене их на эквивалентные бесконечно малые. Этот факт дает возможность при нахождении пределов заменять бесконечно малые на эквивалентные им функции, что может сильно упростить вычисление пределов.

Пример. Найти предел lim

tg5x

sin 7x

x 0

Так как tg5x ~ 5x и sin7x ~ 7x при х 0, то, заменив функции эквивалентными бесконечно малыми, получим:

Пример. Найти предел lim

 

 

 

 

x 0

 

2 x

x

2

Так как 1 – cosx = 2sin

 

 

~ 2

 

 

 

 

 

 

2

2

 

Пример. Найти предел lim

x 0

lim

tg5x

lim

5x

 

5

sin 7x

7x

7

x 0

x 0

 

 

x3

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

1 cos x

 

 

 

 

 

 

 

при х 0, то lim

x3

lim

 

x3

 

lim 2x 0 .

 

1 cos x

 

x 2

 

 

 

x 0

x 0

 

x 0

 

 

 

 

 

 

2

 

 

tgx

lim

x

.

sin x2

x2

x 0

 

Если и - бесконечно малые при х а, причем - бесконечно малая более высокого порядка, чем , то = + - бесконечно малая, эквивалентная . Это можно

 

 

 

 

 

 

доказать следующим равенством lim

 

lim 1

 

 

 

1.

 

 

x a

x a

 

 

 

Тогда говорят, что - главная часть бесконечно малой функции .

Пример. Функция х2 +х – бесконечно малая при х 0, х – главная часть этой функции. Чтобы показать это, запишем = х2, = х, тогда

lim

x 2

0, lim

x 2

x

lim (x 1) 1.

x

 

x

x 0

x 0

 

x 0

Некоторые замечательные пределы.

Первый замечательный предел. lim P(x) , где P(x) = a0xn + a1xn-1 +…+an,

x Q(x)

Q(x) = b0xm + b1xm-1 +…+bm - многочлены.

 

 

x n (a

 

 

a1

...

 

an

)

 

a

 

 

a1

...

an

P(x)

0

 

 

 

 

 

0

 

 

 

 

 

 

 

 

x

 

 

x n

x n m

 

 

 

x

 

 

xn

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Q(x)

 

x m (b

 

 

b1

 

....

bm

)

 

b

 

 

b1

 

...

bm

 

 

 

 

 

 

 

 

 

 

0

 

 

x

 

 

x m

 

0

 

 

x

 

x m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

a1

...

an

 

 

 

 

0

x

x n

 

 

a0

 

 

 

 

 

 

 

lim

 

 

 

 

 

 

 

 

 

 

b1

 

bm

 

 

x

b0

 

...

 

 

b

 

 

 

 

 

 

0

 

 

 

 

 

x

 

x m

 

 

 

 

 

 

 

 

 

при

n m

 

 

 

 

0,

 

 

 

P(x)

a

0

 

 

 

Итого:

lim

 

 

 

, при

n m

 

 

 

 

 

x Q(x)

 

b

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

,

при

n m

 

 

 

 

 

Второй замечательный предел. lim sin x 1

x0 x

 

 

 

1

x

e

Третий замечательный предел.

lim 1

 

 

 

 

x

 

x

 

 

 

 

Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.

Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:

lim

ln(1 x)

1;

lim

a x 1

ln a;

lim

(1 x)m 1

m.

 

 

 

 

 

x0

x

 

x0

x

 

x0

x

 

Пример. Найти предел.

lim

tgmx

lim

mx

 

m

 

 

 

x0

sin nx

x0

nx

 

n

Пример. Найти предел.

lim

tgx tgx0

lim

sin(x x0 )

lim

sin(x x0 )

lim

1

1

1

 

 

 

 

 

 

2

 

x x0

x x0

x x0

(x x0 ) cos x cos x0

x x0

x x0

cos x cos x0

 

cos

x0

 

 

 

x x0

 

 

 

 

 

Пример. Найти предел.

 

 

 

 

 

2

 

sin( / 4 x)

 

 

 

 

 

 

 

 

 

 

 

sin x cosx

 

 

 

 

 

 

sin( / 4

x)

 

1

 

lim

 

lim

2

 

 

 

lim

 

 

4x

 

 

 

 

 

 

 

 

 

 

 

 

 

x / 4

 

x / 4

 

 

 

 

4x

x / 4

2

 

x)

 

2 2

 

 

 

 

 

 

 

 

 

 

 

 

2( / 4

 

 

 

Пример. Найти предел.

 

 

y / 2 x

 

 

cos( / 2 y)

 

 

 

 

 

cos x

 

 

 

 

 

sin y

 

1

lim

 

x / 2

y

 

lim

 

lim

 

 

 

2x

 

 

 

x / 2

 

 

 

y 0

2 y

y 0

y

 

2

 

 

2x 2 y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пример. Найти предел.

 

x 3

x 3

 

 

x 1

 

 

x 3

y x 1

 

y 4

 

y 4

 

 

 

 

y

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

lim

 

 

 

 

 

 

 

lim

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

x 1

 

 

 

lim

y

 

 

lim 1

y

 

 

lim 1

x x

1

 

 

x

 

 

 

 

 

 

 

 

y

 

 

y

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

1

 

4 z

 

 

 

 

1

 

z 4

 

4

 

 

 

 

 

 

 

 

 

 

z

 

 

 

lim 1

 

 

 

 

 

lim 1

 

 

e

 

 

 

 

 

 

 

 

 

 

 

 

z

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

z

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 cos2 x0

44

y

Пример. Найти предел lim

x 2

6x 8

.

x 2

8x 12

x 2

 

Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби.

Тогда lim

x 2

x2 – 6x + 8 = 0;

x2 – 8x + 12 = 0;

D = 36 – 32 = 4;

D = 64 – 48 = 16;

x1 = (6 + 2)/2 = 4;

x1 = (8 + 4)/2 = 6;

x2 = (6 – 2)/2 = 2 ;

x2 = (8 – 4)/2 = 2;

(x 2)( x 4)

lim

x 4

 

2

 

1

(x 2)( x 6)

x 6

4

2

x 2

 

 

Пример. Найти предел.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 x x 2 1 x x 2

 

 

 

 

 

 

 

lim

 

 

 

 

 

 

 

 

 

домножим числитель и знаменатель дроби на сопряженное

 

 

x 2 x

 

 

 

x

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

выражение: lim

 

 

1 x x2 1 x x2

lim

 

2x

 

 

 

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x 0 x(x 1)(

1 x x2 1 x x2 )

x 0 x(x 1)(

1 x x2

 

1 x x2 )

=

 

 

 

2

1 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 (1 1)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пример. Найти предел.

lim

x 2 5x 6

x 2

5x 6 (x 2)( x 3) lim

(x 2)( x 3)

 

3

2

 

1

x 2 9

(x 3)( x 3)

3

3

6

x 3

 

x 3

 

 

Пример. Найти предел lim

x3

6x 2 11x 6

.

 

x 2 3x

2

x 1

 

 

Разложим числитель и знаменатель на множители. x2 – 3x + 2 = (x – 1)(x – 2)

x3 – 6x2 + 11x – 6 = (x – 1)(x – 2)(x – 3), т.к.

x3 – 6x2 + 11x – 6 x - 1

x3 – x2

x2 – 5x + 6

-5x2 + 11x

-5x2 + 5x

6x - 6

6x - 6

0

x2 – 5x + 6 = (x – 2)(x – 3)

Тогда lim

(x 1)( x 2)( x 3)

2

(x 1)( x 2)

x 1

 

Пример. Найти предел.

 

 

 

 

 

 

2sin

2a 2h

cos

2h

2sin(a h)

 

 

 

sin(a 2h) 2sin(a h) sin a

 

 

 

 

2sin(a h)(cosh 1)

 

 

2

2

 

lim

 

 

 

 

lim

 

 

 

 

 

 

lim

 

 

 

h2

 

 

 

 

h2

 

h2

h 0

 

 

 

h 0

 

 

h 0

 

2 lim sin(a h) lim

2sin 2 (h / 2)

2sin a ( 1/ 2) sin a

 

 

 

 

4(h / 2)2

 

 

 

 

 

h 0

h 0

 

 

 

 

 

 

 

 

 

 

Для самостоятельного решения:

1)

lim

2x 4

2x 2

5x 6

 

 

x3

2x 2

7x 1

 

 

x

 

 

2)

lim

(2x3 4x 5)(x2 x 1)

2

 

 

2x3

7x2 x 1)

 

x (x 2)(x4

 

3)

lim

 

x 2

7x 10

 

3

 

 

 

 

 

 

 

 

 

 

 

 

x 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x 2

8x 12

4

 

 

 

 

 

 

 

 

 

 

 

4)

lim

 

 

4 x x 2

2

 

1

 

 

 

 

 

 

 

 

 

 

 

x 1

 

 

 

 

 

4

 

 

 

 

 

 

 

 

x 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5)

lim

 

1 x sin x 1

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x 0

 

 

 

 

x 2

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

6)

lim

 

 

 

 

 

x

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x 0

3 1

x 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 x x 2 7 2x x 2

 

 

 

 

 

 

7)

lim

 

 

 

 

 

7

 

 

 

 

 

 

 

 

 

x 2

2x

 

 

 

 

 

4

 

 

 

x 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8)

lim

 

 

 

 

 

x3 2x 2 4x 8

 

- не определен.

 

 

 

 

16 x3

24 x 2 16

 

x 2 3x 4

 

 

 

 

 

 

 

Непрерывность функции в точке.

Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.

lim f (x) f (x0 )

x x0

Тот же факт можно записать иначе: lim

f (x) f ( lim x)

x x0

x x0

Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.

Пример непрерывной функции:

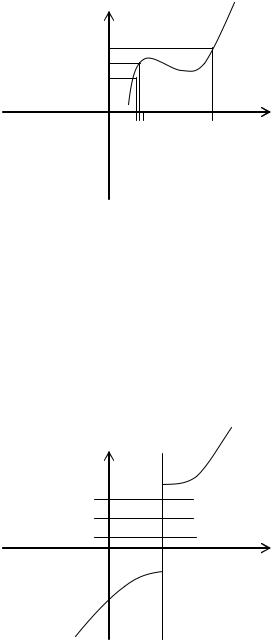
y

f(x0)+

f(x0)

f(x0)-

0 x0- x0 x0+

x

Пример разрывной функции:

y

f(x0)+ f(x0)

f(x0)-

x0 x

Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих условию

x x0

верно неравенство

 

f (x) f (x0 )

 

.

 

 

Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.

f(x) = f(x0) + (x)

где (х) – бесконечно малая при х х0.

Свойства непрерывных функций.

1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.

2) Частное двух непрерывных функций

f (x)

– есть непрерывная функция при

g (x)

 

 

условии, что g(x) не равна нулю в точке х0.

 

 

3) Суперпозиция непрерывных функций – есть непрерывная функция.

Это свойство может быть записано следующим образом:

Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.

Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.

Непрерывность некоторых элементарных функций.

1) Функция f(x) = C, C = const – непрерывная функция на всей области определения.

2) Рациональная функция f (x)

a

0

xn a xn1

... a

n

 

 

1

 

непрерывна для всех

b xm b xm 1

... b

 

0

1

m

 

значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.

3) Тригонометрические функции непрерывны на своей области определения.

Докажем свойство 3 для функции y = sinx.

Запишем приращение функции y = sin(x + x) – sinx, или после преобразования:

 

x

x

y 2 cos x

sin

 

 

2

2

 

 

 

x

x

 

 

 

 

 

lim y 2 lim cos x

sin

 

 

0

 

 

 

 

 

 

 

 

2

2

 

 

 

 

 

 

x0

x0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

x

. При

Действительно, имеется предел произведения двух функций cos x

и sin

 

 

 

 

 

 

 

 

 

2

2

 

этом функция косинус – ограниченная функция при х 0

 

 

x

 

1, а т.к.

 

 

 

 

 

 

 

cos x

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

предел функции синус lim sin

x 0 , то она является бесконечно малой при х 0.

 

x 0

2

 

 

 

 

 

 

 

 

 

 

Таким образом, имеется произведение ограниченной функции на бесконечно малую, следовательно это произведение, т.е. функция у – бесконечно малая. В соответствии с рассмотренными выше определениями, функция у = sinx – непрерывная функция для любого значения х = х0 из области определения, т.к. ее приращение в этой точке – бесконечно малая величина.

Аналогично можно доказать непрерывность остальных тригонометрических функций на всей области определения.

Вообще следует заметить, что все основные элементарные функции непрерывны на всей своей области определения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности